Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques SupérieurOn parle exclusivement de maths, pour le supérieur principalement, les BTS, IUT, prépas... BTSForum de maths BTS AlgèbreTopics traitant de algèbre [tout]Lister tous les topics de mathématiques
Niveau BTS
Partager :

suites

Posté par Profil amethyste 14-08-19 à 14:45

Bonjour, merci d'avance

une question comme ça en passant car en fait je dois bosser la logique mais je prends un peu de temps pour "faire" un peu de maths

Avez vous connaissance d'une formulation du coefficient  binomial \dbinom {n}{p} utilisant entre autre les suites récurrentes linéaires d'ordre 2 ?

donc dans sa formulation on aurait entre autre des matrices

j'ai bien quelques petits résultats qui m'ont l'air intéressants (exploitables pour trouver d'autres résultats)  mais si vous avez connaissance de ça peut être pourriez vous m'en dire un peu plus...

Posté par
carpediemre : suites 14-08-19 à 15:07

salut

ben le problème c'est que tu as deux paramètres ... mais tu as toujours {n \choose k} + {n \choose k + 1} = {n + 1 \choose k + 1}

ce qui permet de passer si on veut de (n, k) à (n, k + 2) ou de (n, k) à (n + 2, k + 1) ... et plus généralement de (n, k) à (n + p, k + q) ...

il suffit d'écrire les choses ... mais est-ce intéressant ? (ce ne sera qu'une formule ...)

Posté par Profil amethystere : suites 14-08-19 à 15:23

Bonjour Carpédiem

pour l'instant j'ai pas grand chose mais comme je vois que  j'arrive à continuer à partir de ce que j'ai déjà,  je me dit que ça se trouve il y a un truc sur internet (en ce qui me concerne sur google j'ai rien trouvé ) :

En fixant n, sur une colonne sur p (du triangle de Pascal ) là j'en suis à  trois lignes de la colonne,  et pour ces trois j'ai une formule qui comprends entre autre un produit d'une matrice 2x2 par une matrice colonne (de deux lignes)

en augmentant p d'une unité (mais en laissant fixe n) il faut augmenter l'exponentielle de la matrice 2x2 d'une unité

ceci dit là je dois bosser la logique (je ne vais pas vite )

bah sinon si j'arrive à faire un truc pas trop moche sans Sigma (sommation) et sans Pi (produit) , je le posterais ici    


Posté par Profil amethystere : suites 14-08-19 à 15:31

erreur je voulais dire le contraire

en fixant p et en augmentant n d'unité en unité  (on reste sur la colonne de n)

bon à plus tard on verra bien

___________________

NB: ceci dit la formule \dbinom {n}{p}=\dfrac {n!}{\left(n-p\right)!.p!} utilise un Pi(produit) même si il n'est pas écrit implicitement

si on peut s'en passer sans toutefois se retrouver avec un Sigma (sommation )  sur les bras en échange...

Posté par Profil amethystere : suites 14-08-19 à 15:33

coquille de plus

je voulais dire : on reste sur la colonne de p

Posté par Profil amethystere : suites 14-08-19 à 23:40

un exemple concret

bon je n'ai pas trop le temps de simplifier (en fait je dois bosser la logique , je fais ça  quand j'en ai assez comme ça de la logique pour la journée)

p\in \mathbb {N}^*

ça ne se voit pas trop mais dans le membre de gauche de l'égalité c'est une matrice colonne 2x1 avec l'expression de deux binômes


\begin {pmatrix}\dbinom {2p+1}{2p-1}\\  \dbinom {2p+2}{2p-1}\end {pmatrix}=\begin {pmatrix}0&1\\p&p\end {pmatrix}^3.\begin {pmatrix}1\\1\end {pmatrix}+\begin {pmatrix}0\\  p-\sum _{p}^{i=1}\left(i.\left(2+\left(4.\left(p-i\right) \right)\right)\right)   \end {pmatrix}

Posté par Profil amethystere : suites 15-08-19 à 00:00

lol j'ai inversé la notation indicielle

\begin {pmatrix}\dbinom {2p+1}{2p-1}\\  \dbinom {2p+2}{2p-1}\end {pmatrix}=\begin {pmatrix}0&1\\p&p\end {pmatrix}^3.\begin {pmatrix}1\\1\end {pmatrix}+\begin {pmatrix}0\\  p-\sum _{i=1}^{p}\left(i.\left(2+\left(4.\left(p-i\right) \right)\right)\right)   \end {pmatrix}

Posté par
lafol Moderateurre : suites 15-08-19 à 00:27

bonsoir
tu trouveras peut-être des pistes là dedans (et sinon, plein de propriétés amusantes des coeff binomiaux)

Posté par Profil amethystere : suites 15-08-19 à 00:41

Bonsoir et merci La Pasi Fol

merci super lien , on n'en fini plus …(je n'ai pas encore tout terminé de regarder)

Belle soirée à vous

Posté par Profil amethystere : suites 15-08-19 à 22:16

Bonjour et merci d'avance

comme c'est en rapport avec ce sujet je pose cette dernière petite question ici

y a t-il un nom générique à ce genre de suite \left(u_n\right) à valeur sur un corps?  

comme on peut le voir dans la figure ci-dessous

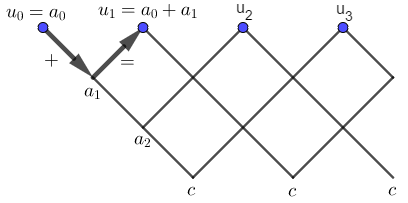
suites

Cette suite \left(u_n\right) se construit de la façon suivante

On se donne une suite finie \left(a_0,a_1,...,a_k\right)

et une constante c

en suivant la procédure décrite par cette figure

______________________

en fait je cherche à savoir comment s'appelle ce genre de suite

ou comment on pourrait les appeler car dans mon petit cahier

parlant de ça il faudrait que j'écrive de quoi ça parle

sinon je vais avoir ce cahier et je ne saurais pas de quoi ça parle ...  

Posté par
lafol Moderateurre : suites 15-08-19 à 22:49

est-ce que tu peux préciser un peu ? par exemple, u_2, c'est quoi ? et u_3 ?

Posté par Profil amethystere : suites 15-08-19 à 22:58

Bonjour et merci La pasi fol

en suivant la procédure de la figure (selon les flèches avec les indications + et =)

u_2=a_1+a_2

u_3=u_2+\left(a_1+a_2\right)+\left(a_2+c\right)

je cherche un nom pour cette suite mais si elle n'en a pas comment l'appeler?

elle est construite avec une constante c et une  suite finie \left(a_n\right)

Posté par Profil amethystere : suites 15-08-19 à 23:01

coquille mince

u_2=u_1+\left(a_1+a_2\right)

u_3=u_2+\left(a_1+a_2\right)+\left(a_2+c\right)

Posté par Profil amethystere : suites 15-08-19 à 23:14

dans mon dernier message j'ai corrigé une coquille pour décrire u_2 et u_3

la raison pour laquelle je voudrais connaître son nom c'est qu'en augmentant l'exponentielle de la matrice carrée à chaque fois on se retrouve toujours avec ce genre de suite à partir de l'exposant 3

sur mon cahier je voudrais placer un titre du genre triangle de pascal et suite "machin"


Posté par
lafol Moderateurre : suites 15-08-19 à 23:18

juste pour être sûre que je pige ce que tu veux faire (ton schéma ne me parle pas, je sais pas pourquoi ?)
u_4 ce serait u_3 + (a_1+a_2) + 2(a_2+c) ?

Posté par Profil amethystere : suites 15-08-19 à 23:28

Merci

ça fait rien (non c'est pas ça)

en partant d'un nœud du graphe tu descend à droite en additionnant puis tu remonte en allant toujours à droite pour écrire la valeur de cette addition

u_4=u_3+a_1+3a_2+3c

avant de l'étudier je voudrais juste lui donner un nom

Posté par Profil amethystere : suites 15-08-19 à 23:36

...ou alors ce que je vais faire c'est ça

dans mon cahier je place mon titre :

une suite particulière et le triangle de Pascal  

et si jamais cette suite possède un nom j'aurais qu'à écrire : et cette suite se nomme blablabla

excusez moi pour l'embêtement … c'est vrai que je fais jamais de brouillon (j'ai tord)

Posté par
lafol Moderateurre : suites 16-08-19 à 00:02

c'est une suite définie par récurrence, mais je sais pas si ce type de récurrence a un nom particulier

Posté par Profil amethystere : suites 16-08-19 à 00:11

Belle soirée à vous La Pasi fol

Je vais faire comme ça ...on verra bien

À propos j'ai trouvé un résultat joli mais lol c'est joli parce que ça fait intervenir mais particulièrement inefficace (comme d'hab souvent avec moi et ce que je trouve lol)

je le placerai ...ceci dit je fais ça pour lâcher un peu la logique avant d'aller au lit

Posté par Profil amethystere : suites 19-08-19 à 20:15

Bonsoir et merci d'avance pour toute info ou signalement d'erreur

En notant S_n^p le nombre de p-partitions d'un ensemble de cardinal n

j'ai obtenu les résultats suivants

S_n^2=2^{n-1}-1

S_n^3=\dfrac {3^{n-1}-2^n+1}{2}

S_n^4=\dfrac {4^{n-1}-3^n+2^{n+1}-2^{n-1}-1}{3!}

S_n^5=\dfrac {5^{n-1}-4^{n}+3^{n+1}-3^{n}-2^{n+1}+1}{4!}

si vous voyez une erreur n'hésitez pas à me le dire

  

Posté par Profil amethystere : suites 19-08-19 à 20:46

NB : là j'ai pas trop le temps (il faut que je bosse la logique, je fais ça en "extra")

j'ai oublié de dire que le tableau est

S_n^p=S_{n-1}^{p-1}+pS_{n-1}^{p}  pour tout n\geq 2 et 2\leq p\leq n

S_n^1=1 et S_n^n=1

je repasserais placer la suite (si ma méthode est correcte )
  


Posté par Profil amethystere : suites 21-08-19 à 06:46

NB+

pour vérifier jusqu'à n=5 et dans la limite de la vingtième ligne du tableau  S_n^p  

j'ai pris la liste A000110 de l'OEIS des nombres de Bell jusqu'à 20

puis j'ai commencé à remplir mon tableau des colonnes 1 à 5

puis j'ai complété le tableau jusqu'à la colonne 20 et la ligne 20

sur chaque ligne j'ai effectué la somme des termes  de chaque colonne

le résultat devant donner le nombre de Bell pour la valeur de la ligne

il n'y avait pas d'erreur (ceci dit si vous en trouvez une n'hésitez pas il se peut qu'elle soit située sur une ligne au delà de la vingtième)  

en ce qui concerne la colonne 6 j'ai été obligé d'écrire autrement ce que j'avais trouvé pour la colonne 5 (on verra bien pour l'instant comme j'ai une piste je continue mais  je fais ça quand j'ai le temps mais si dans une semaine je ne trouve toujours pas cette colonne 6 j'abandonne)  

Posté par Profil amethystere : suites 21-08-19 à 06:48

coquille

amethyste @ 21-08-2019 à 06:46

NB+

pour vérifier jusqu'à n=5 et dans la limite de la vingtième ligne du tableau  S_n^p  

  


je voulais dire

pour vérifier jusqu'à  p=5 et dans la limite de la ….

Posté par Profil amethystere : suites 23-08-19 à 22:25

lafol @ 16-08-2019 à 00:02

c'est une suite définie par récurrence, mais je sais pas si ce type de récurrence a un nom particulier


pourtant cette expression on la retrouve partout(mais vraiment partout quoi…)

en changeant les étiquettes du graphe de la figure du message du 15-08-19 à 22:16(pour le calcul c'est mieux)

a_{k0}=\displaystyle \sum _{i=0}^{k}\dbinom {k}{i}a_{0i}

par exemple \left(b+1\right)^a=\displaystyle \sum _{i=0}^{a}\dbinom {a}{i}b^i

autre exemple

le nombre de surjections de A (de cardinal a) vers B (de cardinal b)

S\left(a,b\right)=b^a-\displaystyle \sum _{k=1}^{b-1}\dbinom {b}{k}S\left(a,k\right)

autre exemple

pour une suite \left(u_n\right) récurrente linéaire d'ordre 2 et à scalaires unitaires

\begin {pmatrix}u_n\\u_{n+1}\end {pmatrix}=\begin {pmatrix}0&1\\1&1\end {pmatrix}^n.\begin {pmatrix}u_0\\u_1\end {pmatrix}

pour n\geq 2k  et k\in \mathbb {N} on a aussi

u_n=\displaystyle \sum _{i=0}^{k}\dbinom {k}{i}u_{n-k-i}

bref en fait dès qu'on parle d'une suite d'un anneau (unitaire ou pas) ça y est, elle est là !!

et c'est normal vu comment est fait le graphe

Posté par Profil amethystere : suites 23-08-19 à 22:48

NB: j'ai peut être exagéré ceci dit lol : faut voir avec la caractéristique de l'anneau

mais bon en ce qui concerne toutes les suites à valeurs réelles on retrouve toujours cette expression qui permet d'exprimer cette suite

Posté par Profil amethystere : suites 24-08-19 à 07:13

Bonjour et merci d'avance

je reste sur ce sujet car ma question est en rapport avec ce sujet (bien que cela ne se voit pas)

ma question :

si je désire parler de l'ensemble de toutes les matrices carrées à coefficients dans \mathbb {R}

la notation de cet ensemble par \displaystyle \underset {i\in \mathbb {N}^*}{\displaystyle \bigcup }\displaystyle \mathbb {R}^{\displaystyle \mathbb {N}_i^*\times \mathbb {N}_i^*}

est correcte n'est-ce pas?

Posté par Profil amethystere : suites 24-08-19 à 07:32

NB

je précise quand même le contexte de ma question

j'ai une bijection

f:\mathbb {R}^{\mathbb {N}}\longrightarrow  \displaystyle \underset {i\in \mathbb {N}^*}{\displaystyle \bigcup }\displaystyle \mathbb {R}^{\displaystyle \mathbb {N}_i^*\times \mathbb {N}_i^*}

si toutefois (et c'est ma question) la notation est correcte  

Posté par Profil amethystere : suites 24-08-19 à 07:35

non je me suis trompé pour ma bijection …

oubliez mon dernier message

la question demeure

Posté par Profil amethystere : suites 24-08-19 à 07:47

il y avait une erreur dans ma bijection

je refais mon post

il s'agissait d'un nota bene de ma question

NB

je précise quand même le contexte de ma question

j'ai une bijection

f:\mathbb {R}^{\mathbb {N}}\longrightarrow  \left(\displaystyle \underset {i\in \mathbb {N}^*}{\displaystyle \bigcup }\displaystyle \mathbb {R}^{\displaystyle \mathbb {N}_i^*\times \mathbb {N}_i^*}\right)^{\displaystyle \mathbb {N}}

voilà pour le contexte de cette question

Posté par Profil amethystere : suites 24-08-19 à 08:02

j'ai relus plusieurs fois la notation employée par mon bouquin d'algèbre (car bon franchement l'erreur est humaine)

c'est ok pour la notation

désolé pour avoir posé ma question pour rien

bonne journée à vous tous

Posté par Profil amethystere : suites 24-08-19 à 11:54

Bonjour

pour en revenir à l'expression du message du 23-08-19 à 22:25

on a la formule du premier ordre  

\forall \left(u_n\right)_{n\in \mathbb {N}}\in \mathbb {R}^{\mathbb {N}}\exists \left(a_n\right)_{n\in \mathbb {N}}\in \mathbb {R}^{\mathbb {N}}\left( u_0=a_0\land u_{n}=\displaystyle \sum _{i=0}^{n}\dbinom {n}{i}a_{i}\right)

Posté par Profil amethystere : suites 04-09-19 à 00:24

Salut

j'ai laissé tombé ma supposition de départ(elle menait à rien)

et là j'ai obtenu ça

\dbinom {n}{p}  =  \displaystyle \sum _{i=0}^{n-p}  ^{i}p

où ici on propose la notation ^{a}b

avec a\in \mathbb {N}  et b\in \mathbb {N}^*

^{0}x  = 1

^{1}x  = ^{0}1  +  ^{0}2  +  ...  +  ^{0}x  =  x

^{2}x  = ^{1}1  +  ^{1}2  +  ...  +  ^{1}x  =  \dfrac {x^2+x}{2}

^{3}x  = ^{2}1  +  ^{2}2  +  ...  +  ^{2}x  = \dfrac {x^3+3x^2+2x}{6}

et ainsi de suite ...


_________________________
démo

En utilisant la formule    \dbinom {n}{p}  =  \dbinom {n-1}{p}  +  \dbinom {n-1}{p-1}  

on obtient   \dbinom {n}{p}  =  \dbinom {p-1}{p-1}  +   \dbinom {p}{p-1}  +  \dbinom {p+1}{p-1}  +  ...  +  \dbinom {n-1}{p-1}  

et donc   \dbinom {n}{p}  =  \displaystyle \sum _{i=0}^{n-p}  \dbinom {p+i-1}{p-1}  

en utilisant cette dernière formule on obtient

(j'ai enlevé les balises car la formule ne passe pas sur le forum)  

   \dbinom {n}{p}  =  \displaystyle \sum _{\displaystyle  \begin{equation}
  \left\{
    \begin{split}
    i=0 \blacktriangleright   n-p\\
    j=0 \blacktriangleright  i\\
    k=0 \blacktriangleright  j     \end{split}
  \right.
\end{equation}}   \dbinom {p+k-3}{p-3}  

et une formule plus générale

(j'ai enlevé les balises car la formule ne passe pas sur le forum)    

\dbinom {n}{p}  =  \displaystyle \sum _{\displaystyle  \begin{equation}
  \left\{
    \begin{split}
    i_0=0 \blacktriangleright   n-p\\
    i_1=0 \blacktriangleright  i_0\\
    i_2=0 \blacktriangleright  i_1\\
    ...\\
    i_{p-1}=0 \blacktriangleright  i_{p-2}  \end{split}
  \right.
\end{equation}}  \dbinom {p+i_{p-1}-p}{p-p}  [/tex]

comme   \dbinom {n}{0}  =  1   et comme   0!  =  1   on obtient

(j'ai enlevé les balises car la formule ne passe pas sur le forum)  

  \dbinom {n}{p}  =  \displaystyle \sum _{\displaystyle  \begin{equation}
  \left\{
    \begin{split}
    i_0=0 \blacktriangleright   n-p\\
    i_1=0 \blacktriangleright  i_0\\
    i_2=0 \blacktriangleright  i_1\\
    ...\\
    i_{p-1}=0 \blacktriangleright  i_{p-2}  \end{split}
  \right.
\end{equation}}   i_{p-1}!^0

et on arrive à ce qui a été posé

Posté par Profil amethystere : suites 04-09-19 à 00:51

re-salut

pour exploiter le dernier résultat (si j'y arrive évidemment)

je vais utiliser l'équation

\displaystyle \sum _{i=1}^{k}i S_i^a = S_k^{a+1} + S_k^1 S_{k-1}^a

-\left\lfloor\dfrac{k-1}{2}\right\rfloor  S_{k-1}^{a+1}-2^a S_{\left\lfloor\dfrac{k-1}{2}\right\rfloor }^{a+1}

-\dfrac {1+\left(-1\right)^k}{2} \left(k-1\right)^{a+1}+T_{2 \left\lfloor\dfrac{k-1}{2}\right\rfloor  }^{a+1}

où les trois expressions ci-dessous sont connues(il faut utiliser les coefficients de Bernoulli)

S_n^a=1^a+2^a+3^a+...+n^a  

T_n^a=2^a+4^a+...+n^a pour n est pair (c'est celui là qu'on utilise dans la formule)

T_n^a=1^a+3^a+...+n^a pour n est impair

Posté par Profil amethystere : suites 04-09-19 à 01:03

coquille

\displaystyle \sum _{i=1}^{k}i S_i^a = S_k^{a+1} + S_k^1 S_{k-1}^a

-\left\lfloor\dfrac{k-1}{2}\right\rfloor  S_{k-1}^{a+1}-2^a S_{\left\lfloor\dfrac{k-1}{2}\right\rfloor }^{a+1}

-\dfrac {1+\left(-1\right)^k}{2} \left(k-1\right)^{a+1}+T_{2 \left(\left\lfloor\dfrac{k-1}{2}\right\rfloor -1\right) }^{a+1}

Posté par Profil amethystere : suites 04-09-19 à 04:27

ah mince non c'est pas ça !!

j'ai été trop rapide à enlever une sommation

je corrige (j'ai vérifié )

\displaystyle \sum _{i=1}^{k}  i  S_i^a  =

S_k^{a+1}  +  S_k^1  S_{k-1}^a  -  \left\lfloor\dfrac{k-1}{2}\right\rfloor   S_{k-1}^{a+1}  -  2^a S_{\left\lfloor\dfrac{k-1}{2}\right\rfloor }^{a+1}

-  \dfrac {1+\left(-1\right)^k}{2}  \left(k-1\right)^{a+1}  +  \displaystyle \sum _{i=1}^{ \left\lfloor\dfrac{k-1}{2}\right\rfloor -1}  S_{2i}^{a+1}


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1675 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !