Inscription / Connexion Nouveau Sujet
Suites et Limites
Je suis en terminale S et j'ai besoin d'aide pour faire mon DM de math
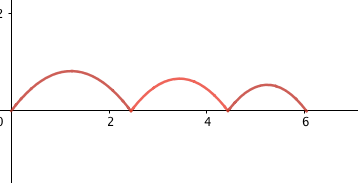
L'énoncé est " Un canon lance une balle rebondissante à partir du point de coordonnées (0;0), situé sur le sol, avec une vitesse initiale (vecteur) v0 de coordonnées (3;4). A chaque fois que la balle retombe au sol, elle rebondit et sa vitesse n'est plus que de 90% de sa vitesse au rebond précédent.
On note (vecteur) Vn, la vitesse de la balle au énième rebond et (An,Bn) les coordonnées
du (vecteur) Vn, exprimé en m/s.
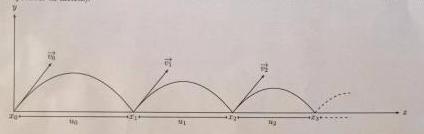
On note Un la longueur du énième rebond et Xn l'abscisse à laquelle se produit ce énième rebond (Un et Xn sont exprimées en mètres)
Questions: 1) Quelle est la nature des suites (An) et (Bn)? en déduire leurs expressions chacune en fonction de n
2) En déduire l'expression de Un en fonction de n.
3) montrer que, pour tout entier naturel n, on a Xn=(24/1,862)*(1-0,81^n)
4) déterminer la limite de la suite (Xn). Donner une interprétation de cette limite pour la balle.
Bonsoir,
1) sa vitesse n'est plus que de 90% de sa vitesse au rebond précédent.
cette phrase te permet de répondre à la question 1)
j'ai trouvé que les suites étaient géométrique de raison 0,9 mais après les autres questions je n'y arrive pas
si tu n'as aucune explication c 'est un problème de physique , ou de cinématique .( une partie du programme de terminale ??)
tu aurais dû la recopier...
les images vont être supprimer
en physique tu n'aurais pas eu la partie A!!!
recopie les formules données dans la partie A
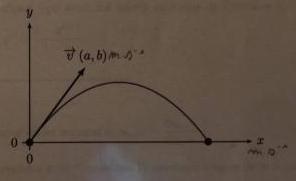
x et y dépendent des coordonnées du V(a,b)
exprime les en fonction de (An) et (Bn)
tu as fais la partie A
comment as-tu trouvé la réponse à cette question:
A quelle distance du point de départ la balle retombe-t-elle au sol ?
avec V_0 (4;3)
pour la partie B
Vn=(.An;Bn)
or An=.....
et Bn=....
même démarche pour trouver Un, la longueur du énième rebond
pour répondre a la question de la partie A j'ai remplacé G dans les formules car il était donné et j'ai fias une équation pour trouver que la balle atterrissait a x=ab/4,9
je ne me suis pas servi du vecteur, donc ça doit être pour ça que je ne comprend pas
c'est juste mais tu ne te souviens comment tu as trouvé cette formule
x=at
quand la balle retombe au sol que vaut y?
cela te permet de trouver" t" en fonction de a puis" x" en fonction de a et b
y= 0
car t=ax c'est ça ????
mais la j'ai trouvé des choses:
an=an-1*90/100 donc an+1=an*90/100
bn=bn-1*90/100 donc bn+1=bn*90/100
v1=(2,7;3,6)
v2=(2,43;3,24)
C'est pour Un que je galère maintenant (merci pour votre aide)
y= 0
car t=ax c'est ça ???? x=at
mais la j'ai trouvé des choses:
an=an-1*90/100 donc an+1=an*90/100
bn=bn-1*90/100 donc bn+1=bn*90/100
v1=(2,7;3,6)
v2=(2,43;3,24)
la balle retombe quand y=0
==> t que tu reportes dans x
pour Un= x quand a=An et b=Bn
Xn=U0+U1+...+Un
oui , c'est seulement le longueur du énième rebond
tu as bien compris qu'il faut en premier déterminer t puis reporter dans x=at
tu reprends au rebond n
\vec{V_n} a pour coordonnées (An,Bn
la balle retombe au sol quand y=0
y_n=\dfrac{1}{2}gt^2+B_nt=0
tu factorises y=0 si t=....
tu reportes dans x_n=U_n=A_nt
pour le 2 si je fais
un=(an*bn)/4,9
=((3*0,9^n)*(4*0,9^n))/4,9
=(12*0,9^2n)/4,9
si U1+U2+U3+...+Un-1
Un=(12*O,81^n)/4,9
C'est bon ou pas ???????
pourquoi i U1+U2+U3+...+Un-1 ?????????
pour le 2 si jtu fais plut^t ça
un=(an*bn)/4,9 ( à justitier voir partie A...)
=((3*0,9^n)*(4*0,9^n))/4,9
=(12*0,9^2n)/4,9
Un=(12*0,81^n)/4,9 tu
et pour terminer :
Xn=U1+U2+U3+...+Un
2) En déduire l'expression de Un en fonction de n.
tu n'es pas sûr d'avoir répondu à cette question
question 3
et pour terminer :
Xn=U1+U2+U3+...+Un