Inscription / Connexion Nouveau Sujet
tache complexe cosinus
je suis bloquer a cause d'un angle, je doit aider un architecte a construire un escalier information : angles d'ouverture : 30 à 35 degrés selon les normes
hauteur de la main courante : 80 à 96.5 degrés selon les norme
hauteur de la contre marche : 12.5 à 20 cm
largeur de la marche : au moins 90 cm
giron : 23.5-35.5 cm
énoncé:
le nouvel escalier du collège doit relier le rez-de-chaussée au couloir du première étage situé 6m plus haut
aidez l'architecte à réaliser le plan de cet escalier; vous préciserez le nombres de marches, leurs dimensions, la longueur de la rampe ect.. merci de votre aide !!
le sujet n'est pas totalement bon dans lequel tu ma donner le lien il faut le refaire en tenant compte de l'angle !
j'ai fait la même erreur mais il faut donné par rapport a se qui est donné pas au norme minimum et maximum
themath, tu es banni pour récidive de "flood"
tu avais été averti hier...
tu recommences....
Tu peux venir sur notre site pour te faire aider pour tes exercices, mais je te demande d'arrêter d'écrire un peu partout comme tu le fais, ces remarques ou bêtises qui ne font pas du tout avancer les sujets.
Réfléchis, tu comprendras que cela ne peut qu'ennuyer la personne que tu cherches à aider, et qui au final a des réponses fausses...
Reviens, mais en respectant le travail des autres. Sinon, la punition sera beaucoup plus longue.
malou (modérateur)
Ensuite, tu dois déterminer:
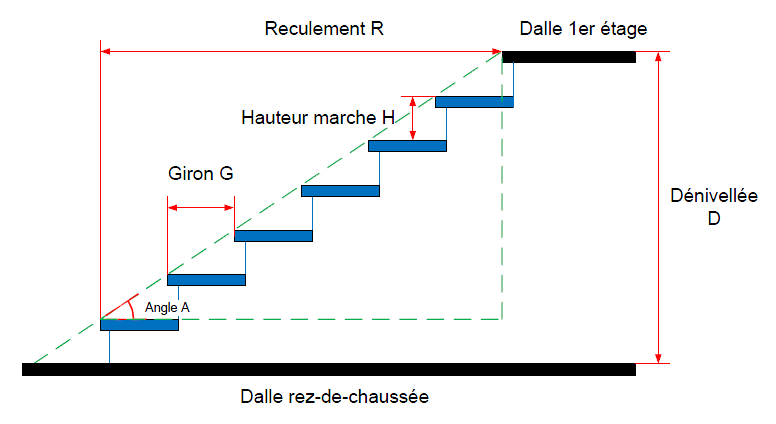
1/ le nombre de marches possibles N sachant que la hauteur de marche H doit être comprise entre 12,5 cm et 20 cm.
2/ le reculement R (ou l'emprise) qui est la distance horizontale entre le nez de la première marche et le nez de marche du palier d'arrivée, sachant que le nez d'une marche est la partie saillante d'une marche (le bord) et que le giron G qui est la distance horizontale entre deux nez de marche doit être compris entre 23,5 cm et 35,5 cm.
Bon travail...
Merci je vais faire avec je vous dit se soir se que j'ai reussi car en se moment je ne suis disponible !! Merci
Themath
Je veut bien vous croire c'est se que j'ai fait mais le probleme c'est que il faut trouver exactement les mesures par exemple pour les marche minimun 30 maximun 48 mais il faut le nombre de marche pour 6 metres de haut comment faire ?
Themath, bonjour.
Bien pour les marches
Comme la dénivelée D, ou hauteur d'escalier, est la distance verticale entre le palier de départ et le palier d'arrivée, alors le nombre de marche est compris entre 30 et 48.
Petite mise à jour du tableau :
Calcul du reculement R (ou l'emprise) qui est la distance horizontale entre le nez de la première marche et le nez de marche du palier d'arrivée.
Le giron G qui est la distance horizontale entre deux nez de marche doit être compris entre 23,5 cm et 35,5 cm.
je vient de comprendre merci beaucoup ! pour pouvoir poursuivre il faut utiliser la hauteur qui est de 6 m de haut mais on a que un seul angle qui est de 90° et que une seul longeur comment pourrai ont calculé pour le cosinus il faut de longeur, celle du coté adjacent et celle de l'hypoténuse mais pour avoir l'hypoténuse il faut deux longueur mais on a pas de mesure précisé on a que les normes comment pourrais ont calculer
je devrais avoir ma copie demain je vous donnerais les resultat trouver du reculement par rapport au nombre de marche maximum et minimum et au giron max et mini ! il me semble avoir utiliser pythagore comme formule. je vous dit demain les resultats @bbomaths ( desolé pour les fautes )
cordialement themath
Themath, bonjour.
Tout d'abord, des excuses pour mon silence.
Voilà, le résultat de mon travail.
Données selon les normes.
Calcul du nombre de marches.
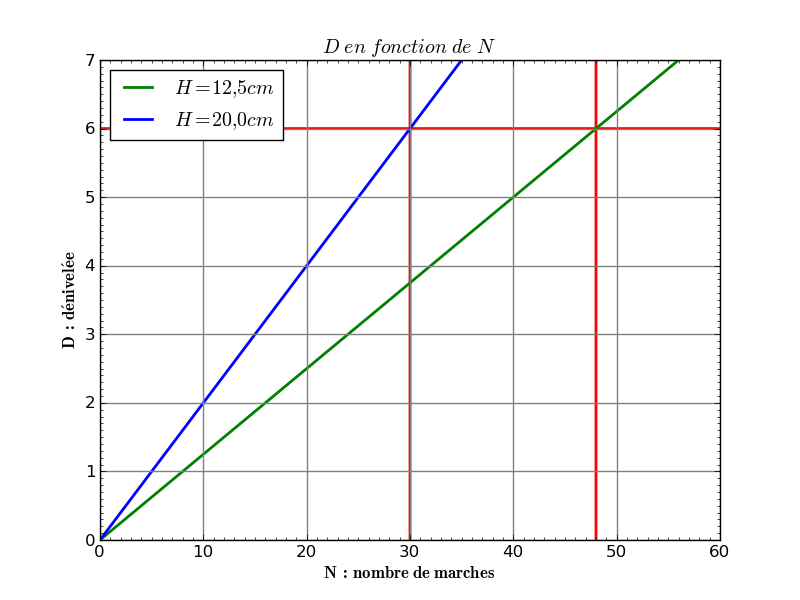
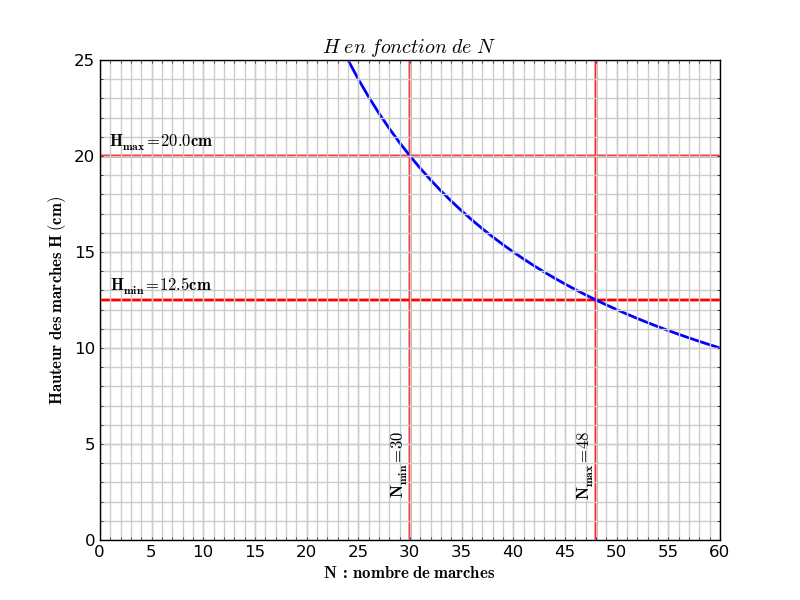
Nous avons une dénivelée D, ou hauteur d'escalier, de 6 m qui est la distance verticale entre le palier de départ et le palier d'arrivée, et les hauteurs de marche H minimale et maximale.
Alors, le nombre de marches N est :
D'où :
Et :
Ainsi, le nombre de marches N est tel que :
On créé un tableau récapitulatif dans lequel on regroupera les données :
Calcul du nombre de girons.
Le giron G est la distance horizontale entre deux nez de marche successifs qui doit être comprise entre 23,5 cm et 35,5 cm. Le nombre de girons est égal au nombre de marches moins 1.
On met le tableau à jour :
Calcul du reculement R (ou de l'emprise).
Le reculement R est la distance horizontale entre le nez de la première marche et le nez de marche du palier d'arrivée et il vaut :
Le reculement maximal vaut :
Le reculement minimal vaut :
On met le tableau à jour :
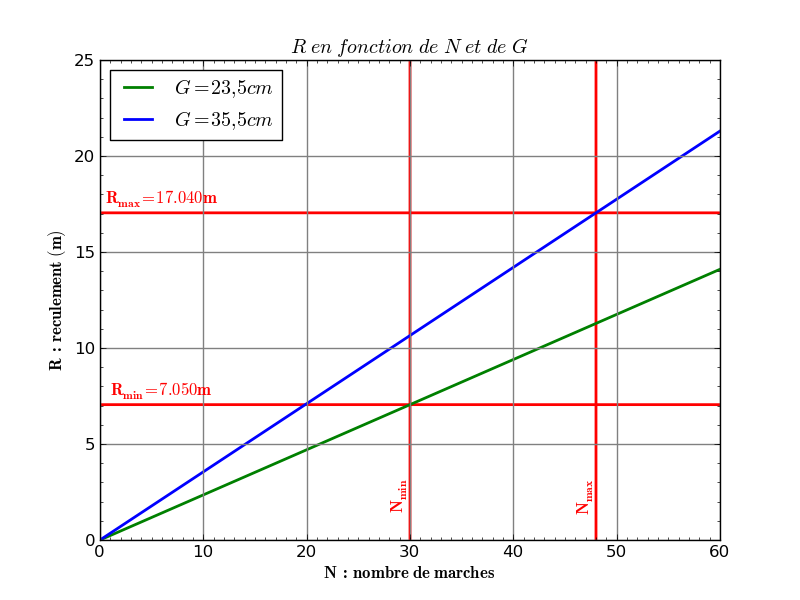
La figure suivante donne le reculement R en fonction du nombre de marches N et des valeurs minimale et maximale du giron G.
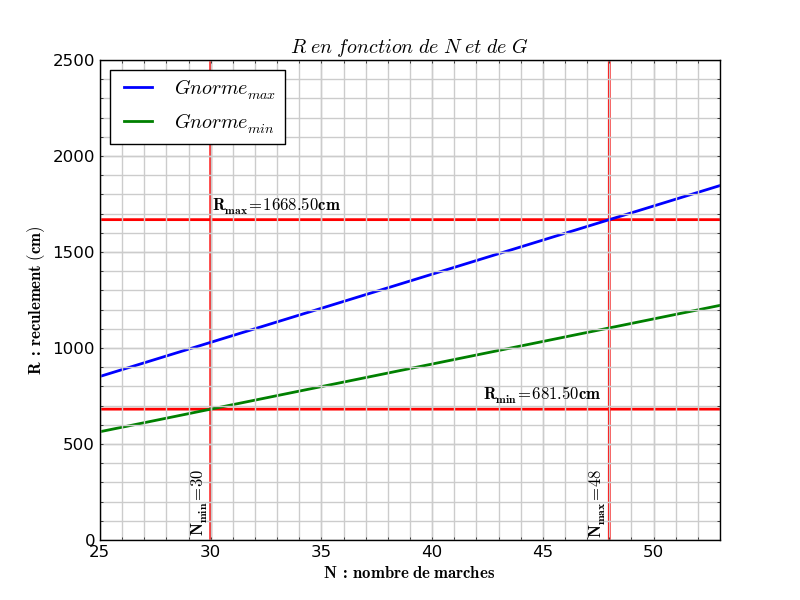
\textbf{Calcul de l'angle A.}
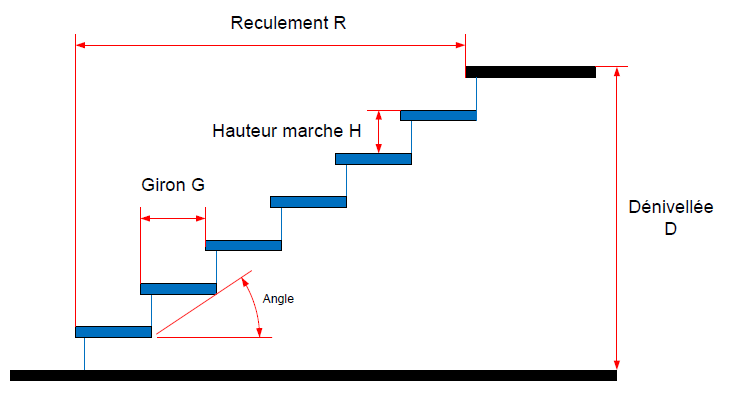
Sur la figure représentant un escalier, on peut remarquer qu'on peut tracer un triangle rectangle dont :
L'hypoténuse serait un segment de droite passant par le nez des marches.
Le côté opposé serait un segment de droite vertical passant par le nez de la plus haute marche et dont la longueur serait la dénivelée moins la hauteur d'une marche.
Le côté adjacent serait un segment de droite horizontal passant par le nez de la plus basse marche et dont la longueur serait le produit du giron par le nombre de girons.
On a alors :
D'où :
L'angle est minimal lorsque le reculement est maximal, inversement l'angle est maximal lorsque le reculement est minimal.
Alors la valeur de l'angle maximal vaut :
Ou :
Ou :
Ou :
Ou :
Et de la même façon pour la valeur de l'angle minimal :
On met le tableau à jour :
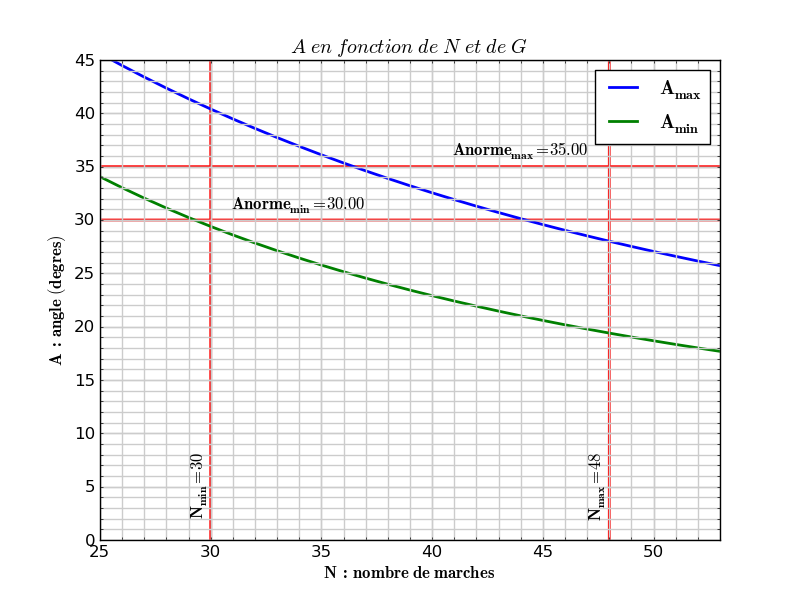
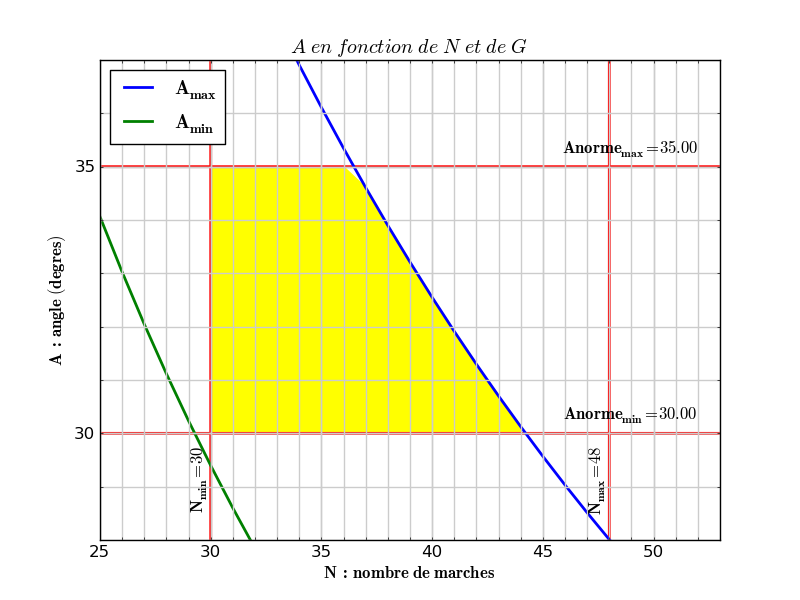
La figure suivante donne la valeur de l'angle A en fonction du nombre de marches N et des valeurs minimale et maximale du giron G.
Sur la figure on a rajouté les valeurs minimale (30°) et maximale (35°) imposées à l'angle par la norme au moyen de deux axes horizontaux.