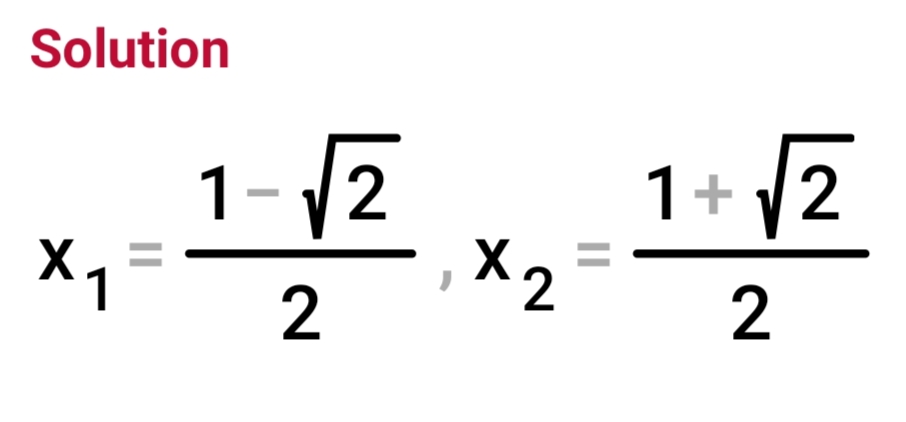Inscription / Connexion Nouveau Sujet
Tangente à une courbe
Bonjour j'ai un exercice et je ne sais pas par où commencer :
On considère la fonction f définie sur R par f(x)=(-4/3) × x**3 +2x**2 + x - 1.
On designe par C sa courbe représentative dans un repère orthonormé.
1) Démontrer que la Courbe C admet deux tangentes parallèles à l'axe des abscisses.
Deja je sais que si f admet un extremun local en a alors f'(a)=0
Et si c'est 0 ça veut dire que la tengante est parallèle a l'axe des abscisses
bonjour,
oui, quand la dérivée s'annule, la tangente à la courbe est // à l'axe des abscisses..
Donc il faut trouver quand la dérivée s'annule..
1ère chose à faire : exprimer f'(x).
vas y !!
Oui, tu es plus ou moins sur la bonne piste.
Quand la dérivée est 0, la tangente est parallèle à l'axe des abscisses.
Et c'est vrai aussi dans l'autre sens : Quand la tangente est parallèle à l'axe des abscisses , alors la dérivée est 0
Ou encore, je redis exactement la même chose : chercher les points où la tangente est parallèle à l'axe des abscisses, c'est la même chose que chercher les points où la dérivée vaut 0.
Là, j'en ai beaucoup dit ! il n'y a plus qu'à poser les calculs.
Arrrgh !
3 messages.
Allez, c'est l'heure du footing, l'exercice devrait être fini quand je reviens.
Je ne suis pas très à l'aise avec le calcul de dérivé donc je ne trouve pas le théorème à appliquer.
Oui : il faut raisonner .
tangente parallele à (OX) , donc coefficient directeur nul .
Or le coefficient directeur d'une tangente à une courbe en un point est egal au nombre dérivé d'où l'equation que tu ecris.
c'est les solutions de l'equation -4x**2+4x+1=0
mais encore ? Ce sont les abscisses de quels points par rapport à la courbe?
Il faut absolument approfondir ton cours :
Si une courbe admet une tangente en un point A ,le coefficient directeur de cette tangente est f'(xA).
Si cette tangente est parallele à OX , f'(xA) = 0
c'est le abscisses des points ou la courbe passe l'axe des abscisses
Non : ne confond pas f(x) =0 et f'(x) =0 d'accord?
J'ai l'impression que Maroui est toujours paumé.
Il faut que tu fasses un dessin de la courbe au brouillon.
Philgr22 parlait de faire un dessin à la calculatrice. C'est une méthode. Tu peux aussi calculer 5 ou 6 valeurs : f(-2), f(-1) f(0), f(1) et f(2) par exemple.
Mais attention, si tu n'es pas très à l'aise en maths, à tous les coups, tu vas faire des erreurs dans les calculs...
Fais les 2 : les calculs de quelques valeurs, le dessin sur ta calculatrice, et tu regardes si ça correspond plus ou moins.
Ensuite, tu as ces 2 valeurs que tu as trouvées : et
Place ces 2 points sur ton graphiques.
Est-ce que tu remarques une '''coïncidence''' ?
En vrai, ce n'est pas une coïncidence, c'est le thème de l'exercice.
Fais le dessin sérieusement, fais tout ça... tu vas combler plein de lacunes d'un coup.
J'avais pas vu qu'il y a une deuxième question :
Déterminer les coordonnées des points en lesquels la tangente à la courbe C est parallèle à la droite D d'équation y=x+3.
Dans la première question, on a cherché les réels x pour lesquels f'(x)=0 : pente = 0, tangente = horizontale.
Maintenant, on cherche les réels x pour lesquels la pente vaut ???
Et donc on doit résoudre l'équation ???
A toi de compléter cette phrase, en remplaçant les ??? par les bons mots ou les bonnes formules
Question 1 : Non. La pente vaut toujours y' ... c'est plus ou moins la définition de la pente.
Question 2 : Non, encore plus non que pour la question 1. Là, tu dis qu'on doit résoudre l'équation y'=y'
On te dit qu'on cherche les points où la tangente est parallèle à la droite d'équation y=x+3 ; cette droite là doit bien intervenir quelque part. Si on avait dit la droite d'équation y=3x+2,ça changeait quelque chose ? Et si on avait dit la droite d'équation y=x-4, ça changeait quelque chose ?
On cherche les points où la tangente à la courbe est parallèle à la droite d'équation y=x+3.
Donc je repose les différentes questions :
Q1 : si on cherchait les points où la courbe est parallèle à la droite y=3x+2, est-ce que ça changerait quelque chose ?
Q2 : si on cherchait les points où la courbe est parallèle à la droite y=x-4, est-ce que ça changerait quelque chose ?
Q3 : compléter cette phrase :
on cherche les réels x pour lesquels la pente vaut ???
Q4 : compléter cette phrase :
Et donc on doit résoudre l'équation ???

 !
!