Inscription / Connexion Nouveau Sujet
Thalès
Bonjour à tous
Quelqu'un pourrait-il m'aider pour cet exercice de 3ème s'il vous plait ? Merci beaucoup d'avance.
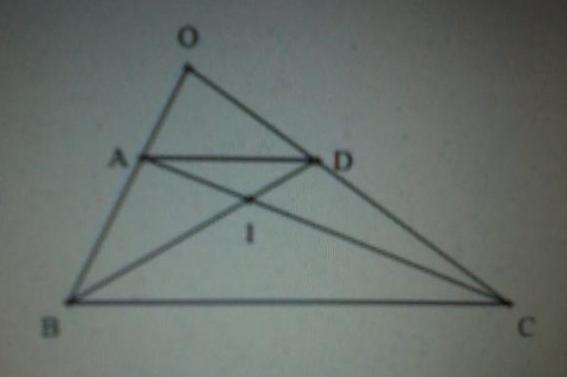
Les droites (AB) et (CD) sont sécantes au point O. Les droites (AC) et (BD) sont sécantes au point I. Les droites (AD) et (BC) sont parallèles. En utilisant deux configurations de Thalès que vous expliciterez, démontrer que : IA sur IC = OA sur OB
Pour l'une, oui.
Précise chaque configuration par les lettres que portent les points d'intersection.
Les droites (AC) et (BD) sont sécantes en I
Les droites (AD) et (BC) sont parallèles
Donc d'après le théorème de Thalès on a : AI sur IC = DI sur IB = AD sur BC
Les droites (AB) et (DC) sont sécantes en O
Les droites (AD) et (BC) sont parallèles
Donc d'après le théorème de Thalès on a :
OA sur AB = OD sur DC
C'est juste, sauf la fraction centrale qui devrait être OA/OB .
Maintenant, considère ce groupe d'égalités et celui de 17h10. Que remarques-tu ?
Alors je peux justifier que IA sur IC = OA sur OB ?
Car c'est ce que je dois démontrer dans l'exercice
Tu as montré que toutes les fractions des deux groupes d'égalités étaient égales. Tu peux donc conclure.



