Inscription / Connexion Nouveau Sujet
Tracer des vecteurs
Bonjour, j'ai un DM à faire pour la rentrée.. Le problème, c'est que je n'y arrive pas du tout ! Je n'ai pu faire aucune réponse ! Pouvez vous m'aider ? Ce serait vraiment très aimable.
Merci d'avance et bonnes fins de vacances pour ceux qui le sont.
Désolée ne pas pouvoir vous renseigner sur mes réponses et pensées, je suis perdue..
Si quelqu'un pouvait m'expliquer comment l'on fait exactement, avec des vecteurs qui ne se touchent absolument pas, et qui sont très différents pour les additionner et les soustraire.. Merci beaucoup.
Exercice 1
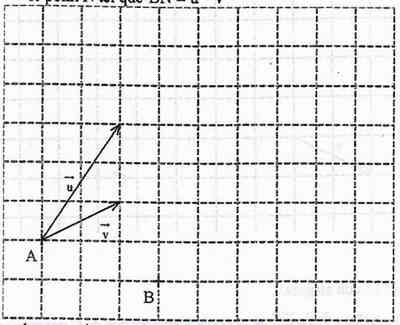
Placer : le point M tel que vectAM =  +
+ 
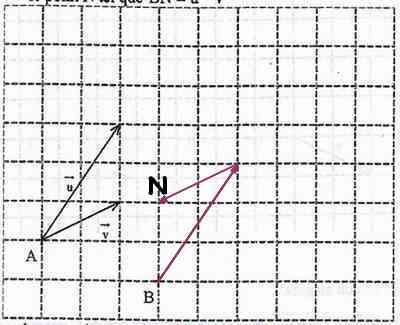
le point N tel que vectBN =  -
- 
Voir Figure 1 ci dessous
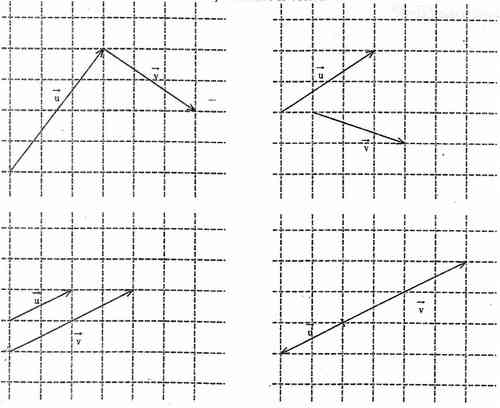
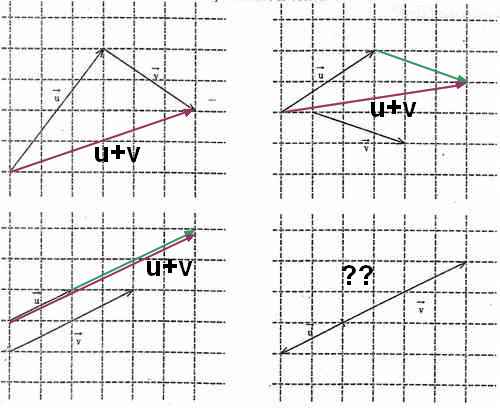
Dans chacun des cas suivants, construire le vecteur  +
+ 
Voir Figure 2 ci dessous
Exercice 2
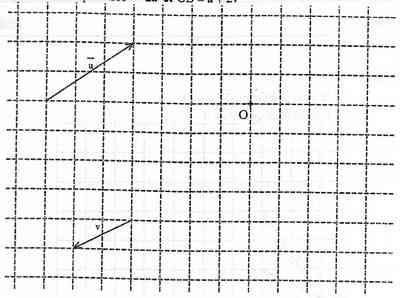
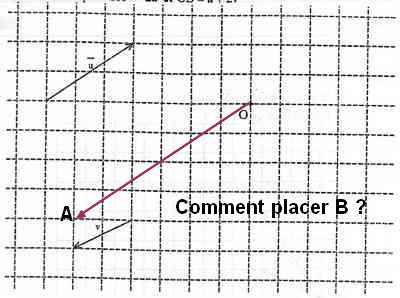
Placer les points A et B tels que : vectOA = -2 et vectOB =
et vectOB =  + 2
+ 2
Voir Figure 3 ci dessous
Exercice 3
Soient trois points A, B et C non alignés.
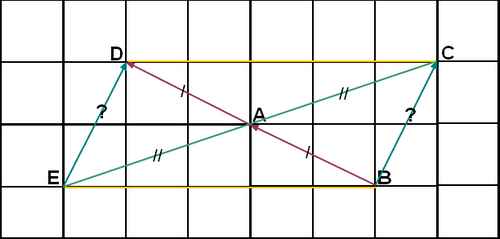
1) Placer le point D vérifiant vectBA = vectAD et le point E symétrique de C par rapport à A.
2) Démontrer que vectED = vectBC
Merci beaucoup de votre aide et soyez indulgents SVP cette année j'ai un peu de mal car j'ai beaucoup été absente.. J'espère ne pas trop demander.. Pouvez vous seulement m'indiquer et m'expliquer comment faire pour que je puisse ainsi trouver les réponses moi-mêmes et après vous demander si j'ai bon.. Merci encore.
bonsoir,
pour réaliser le premier exercice il suffit en partant du point A de tracer u et de ce point completer par v
pour l'exercice 1 en partant de A il faut tracer u (ce qui est fait dans l'énonce) puis (v) en partant de u et M se trouve a la fin
pour N c la même démarche en partant de B il faut tracer u puis (-v) a partir de u tracé et N se trouve a la pointe de -v
c bon pour tracer -v?
Ha oui mais comment tracer -v ??
Thomaszz : Oui j'ai déjà entendu parler de cette relation AB + BC = AC
Le problème c'est qu'entre la règle des parallélogrammes et la relation de Chasles, mon professeur explique très mal et finit par tous nous embrouiller en classe !
ton vecteur v estorienté dans le sens de ta fleche -v estsur la droite passant par se vecteur mais orienté dans son sens inverse et de meme norme
bonjour,
voila c'est ca maintenant il suffit juste de tracer BN
le principe reste le meme pour le restant des exercices
Voici ce que j'ai fait.
Pour l'image 1, je n'y arrive pas au 4e cas.
Pour l'image 2, je n'y arrive pas à la 2e consigne.
Pour la dernière image, je crois tout avoir bien fait. Pour la démonstration, je dois utiliser la règle des parallélogrammes et des vecteurs qui sont égaux ??
Merci.
bonsoir,
désolé mais j'ai du mal à me retrouver sur les schémas les deux premiers sont justes, il represente AM et BN.
le troisieme et 4 dessin appartiennent a quelle consigne.
et pour OA je suis d'accord pour placer B ce n'est pas compliqué en partant de O il faut tracer u puis de ce point 2v
Cette image : 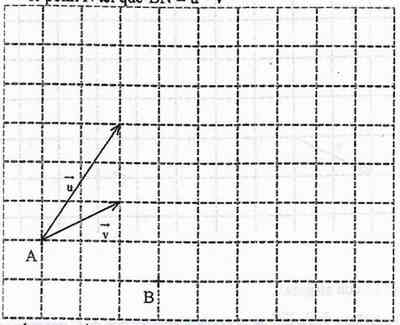 appartient à la consigne : Placer : le point M tel que vectAM =
appartient à la consigne : Placer : le point M tel que vectAM =  +
+  et le point N tel que vectBN =
et le point N tel que vectBN =  -
- 
Cette image : 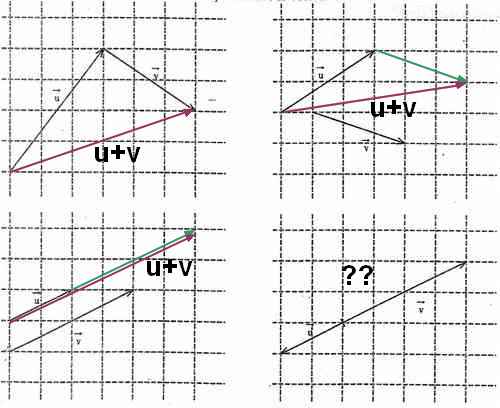 appartient à la consigne : Dans chacun des cas suivants, construire le vecteur
appartient à la consigne : Dans chacun des cas suivants, construire le vecteur  +
+ 
Cette image : 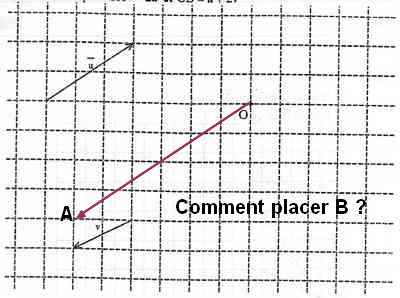 appartient à la consigne : Placer les points A et B tels que : vectOA = -2
appartient à la consigne : Placer les points A et B tels que : vectOA = -2 et vectOB =
et vectOB =  + 2
+ 2
Cette image : 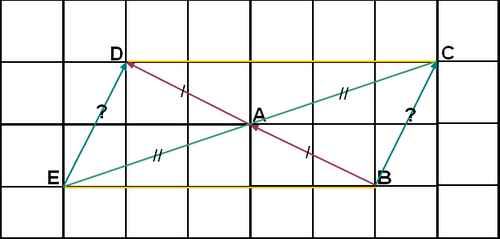 appartient à la consigne : Soient trois points A, B et C non alignés.
appartient à la consigne : Soient trois points A, B et C non alignés.
1) Placer le point D vérifiant vectBA = vectAD et le point E symétrique de C par rapport à A.
2) Démontrer que vectED = vectBC
Pour la première image, j'ai tout fait.
Pour la deuxième image, il me manque une chose, et est-ce que j'ai bon ?
Pour la troisième image, je n'arrive pas à tracer OB
Pour la dernière image, j'ai fait la figure, est-elle bonne, et pour démontrer dois-je bien utiliser la règle des vecteurs égaux et des parallélogrammes ?
J'espère que c'est + clair maintenant, merci d'avance ! 
bonjour,
pour placer AM et BN c'est comme pour construire les vecteurs qui ont ete fait juste apres en partant de A tracer u puis de ce nouveau point il faut tracer v
BN c'est identique sauf qu'il faut utiliser -v (vecteur de même norme, valeur, mais de direction opposée).
Pour le troisième graphique u et v sont colinéaire donc leur somme se retrouve sur cette même droite mais entre u et v car u est de sens opposé.pour le trouvé simplement a la fin du vecteur v il suffit de tracer u.
Pour trouver B dans le 4eme graphique de la même manière que A a été trouvé en partant du point O il faut tracer u puis de ce nouveau point 2v.
Pour le dernier énoncé la figure est juste et utilisé la réglé des vecteurs égaux oui mais est ce que dans l'énoncé il est dit que c'est un parallélogramme sinon je pense que c'est a démontrer donc peut être utiliser d'autre propriété de la figure.
Merci beaucoup pour tes éclaircissements, c'est très clair, très bien expliqué et ça m'aide beaucoup à comprendre.
Pour le parallélogramme, effectivement il n'est pas dit que c'en est un mais ses diagonales se coupent leur milieu donc c'est démontrable puisque BA = AD et que EA = AC étant donné que E est le symétrique de C par rapport à A.
Donc si c'est un parallélogramme, il possède 2 côtés égaux et parallèles deux à deux.
Donc je peux prouver ainsi que ED = BC car ils sont parallèles et de même mesure puisqu'ils sont dans le parallélogramme DEBC et que ceux sont 2 côtés opposés.
J'espère que ma démonstration est claire ?
Voici mes réponses pour le graphique où  et
et  sont colinéraires (première image)
sont colinéraires (première image)
Et mes réponses sur le graphique où il faut placer B (deuxième image).
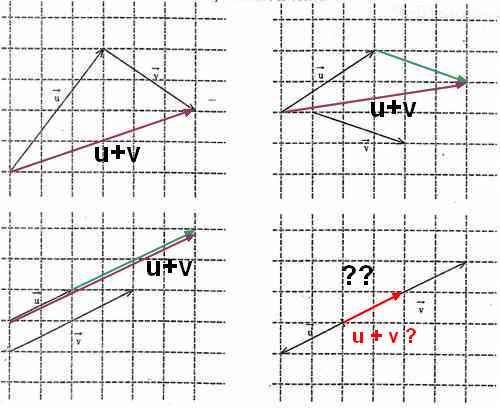
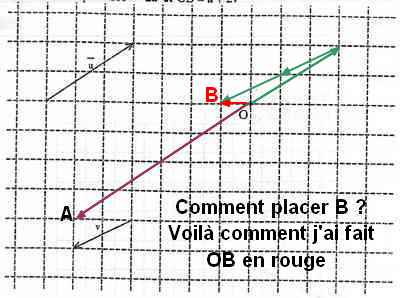
pour OB c'est juste et pour u+v sur le dernier graphique aussi.
Comme tu le dis aussi si EBDC est un parallélogramme alors........
je pense plutôt qu'il faudrait démontrer que les cotés sont respectivement parallèle 2à2 (en démontrant qu'ils sont colinéaire alors se devrait être possible)
Hum, après réflexion, je ne vois pas trop comment démontrer que les côtés sont respectivement parallèles 2 à 2 sans admettre avant ça que c'est un parallélogramme..
Aurais-tu une idée pour me mettre sur la voie ?
Car vu que les diagonales se coupent en leur milieu, on a déjà une piste.
Ensuite, en démontrant que c'est un parallélogramme, on pourra admettre par la suite que les côtés sont parallèles 2 à 2 et ainsi prouver que ED = BC puisqu'ils sont de même mesure et parallèles.
Ca ne revient pas au même ?
Je ne veux pas te contredire mais ce ne serait pas plus simple ma solution ?
Ainsi on prouve que c'est un parallélogramme, et mon professeur en a souvent parlé, donc je pense que je devrais l'utiliser car j'ai peur que ce soit un peu plus long Thales...
Il faudrait en venir à cette conclusion = AE/AC et AD/AB sont égaux mais on n'a pas leurs mesures..
bonjour,
je ne suis pas d accord tu suppose que c'est un parallélogramme (graphiquement ça y ressemble mais aucune hypothèse ne permet de l'affirmer) mais tu n'en sais rien en appliquant la réciproque thales sur ce dessin (3eme configuration) tu prouve que les cotés sont //. c aussi simple et ça ne prend que 4 lignes même pas
Pour le parallélogramme, ses diagonales se coupent leur milieu : BA = AD et EA = AC étant donné que E est le symétrique de C par rapport à A.
oui je suis d'accord mais un parallélogramme n'est pas définis que par des diagonales qui se coupent en leur milieu
Je lis partout dans mes cours et sur internet que dire qu'un quadrilatère a ses diagonales qui se coupent en leur milieu suffit à démontrer que celui-ci est un parallélogramme.. Après cela peut-être un parallélogramme plus précis (rectangle, etc.) si une autre propriété s'y ajoute, mais cela suffit.
Soit on dit que ce quadrilatère a ses diagonales qui se coupent en leur milieu et donc puisqu'on admet ainsi que c'est un parallélogramme, on peut dire que ses côtés sont égaux et parallèles deux à deux.
Soit on dit que ce quadrilatère a ses côtés égaux et parallèles deux à deux et donc puisqu'on admet ainsi que c'est un parallélogramme, on peut dire que ses côtés sont égaux et parallèles deux à deux.
Ce sont les deux principales caractéristiques d'un parallélogramme donc une suffit pour admettre l'autre..
Enfin cela me semble logique et c'est toujours ce que j'ai appris. En fait, l'un entraîne l'autre et inversement.
Voici un site qui me semble juste...
http://jellevy.yellis.net/Classes/Geo_Dynam/const_paralleg.htm
Heu je me corrige :
Soit on dit que ce quadrilatère a ses diagonales qui se coupent en leur milieu et donc puisqu'on admet ainsi que c'est un parallélogramme, on peut dire que ses côtés sont égaux et parallèles deux à deux.
Soit on dit que ce quadrilatère a ses côtés égaux et parallèles deux à deux et donc puisqu'on admet ainsi que c'est un parallélogramme, on peut dire que ses diagonales se coupent en leur milieu...
Je sais pas si j'explique bien ce que je veux dire.. Mais une seule propriété suffit pour prouver que c'est un parallélogramme et cette même propriété entraîne l'autre.