n ou k?

Soit q le ratio de liquide qui reste après prélèvement: q = (Q-1)/Q. Soit a,b,c les quantités respectives de solution A, B et C.
Après les prélèvements et ajouts des trois solutions les quantités évoluent comme :
a -> aq³ + q²
b -> aq³ + q
c -> aq³ + 1

On voit que la quantité de solution A tend exponentiellement vers a' = q²/(1-q³).
Soit x l'écart à la quantité stable: x = a - a'. x évolue comme :
x -> xq³

On a donc au final: a(k) = a' + (a(0) - a') q^3k.

erratum :
a -> aq³ + q²
b -> bq³ + q
c -> cq³ + 1

@LittleFox

Il me semble qu'il y a encore des erreurs dans tes formules .

Personnelement j'arrive ( avec tes notations ) à : qui tend vers quand on réitère les manipulations .

Imod

Nos formules pour f(a) donnent la même chose quand a=b=c.
Mais ce n'est le cas qu'à la première itération.

Ma formule donne les même résultats que mes simulations. Pas la tienne

En effet on a bien qui tend vers l'unique point fixe   .

J'étais bêtement parti sur a->a-1/3 , b->b-1/3 et c->c-1/3 au lieu de a->qa , b->qb , c->qc .

Imod

Edit :

Imod

salut Littlefox , que donne tes proportions pour A ,B et c au bout du 1000 ieme essais (depuis ton algo) ?

@flight
Cette question n'a pas de sens.
1) Je n'ai pas d'algo, juste des petits tests de vérifications à la main sur moins de 10 itérations.
2) 'A' et 'B' sont des noms de solution, 'c' est une quantité de solution.
3) Les proportions a:b:c dépendent de la quantité totale de liquide (Q) qui n'est pas spécifiée.

Je te répondrai donc 0:0:1 en démarrant avec 1 litre de mélange.

re..

1) je voyais dans le fil  que tu parlais de simulation , je pensais que tu avais rédigé un algo
   pour décrire la chose

2)A et B sont des solutions oui je sais c'est meme moi qui a crée le post

3)on peut prendre par exemple Q=  100 litres

Au bout de 1000 itérations, la distance au point stable est multipliée par q³⁰⁰⁰ 8*10^-14.

On peut donc dire qu'on est très proche de ce point stable. A ce point les proportions a:b:c sont de q²:q:1 = 9801:9900:10000.

J'ai essayé de regarder le problème un peu plus dans le détail .

Tout d'abord la limite de chaque quantité de solution dépend uniquement de la quantité totale de liquide et pas de la proportion de chacune . La proportion du troisième produit au bout de n tours est donc   . Ces formules se généralisent aisément pour k solutions .

La convergence vers le point d'équilibre est très rapide :



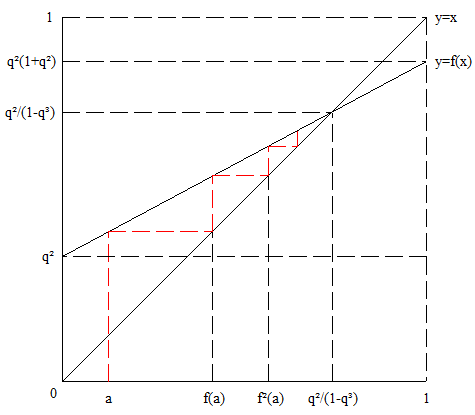
Il y a tout de même un point qui me chagrine , je dois faire une erreur logique mais je n'arrive pas à voir où :

L'équilibre final ne dépend pas des proportions initiales et les manipulations sont les mêmes pour les trois solutions . Commencer par la solution 2 revient simplement à changer la configuration initiale et devrait aboutir au même résultat que de démarrer avec la une mais il y a une permutation des limites .

Imod    

J'ai compris mon erreur ( il suffit souvent de l'écrire pour en voir l'absurdité ) . Les proportions des solutions changent à chacune des trois étapes , c'est seulement les fins d'étapes qui convergent vers une limite .

Imod

Oui, les proportions limites sont toujours 1:q:q²:q³:...:q^m-1 pour m solutions avec d'abord la dernière solution a avoir été versée, puis l'avant dernière, et ainsi de suite.

Les proportions ici données sont à diviser par 1-q^m pour avoir les quantités.

C'est parce qu'on s'arrête toujours après 3 étapes que la symétrie n'est pas apparente.