Inscription / Connexion Nouveau Sujet
triangkles semblalbles
Bonjour,
Cet exercice me pose un problème, je ne suis pas sûre que l'énoncé que voici soit juste.
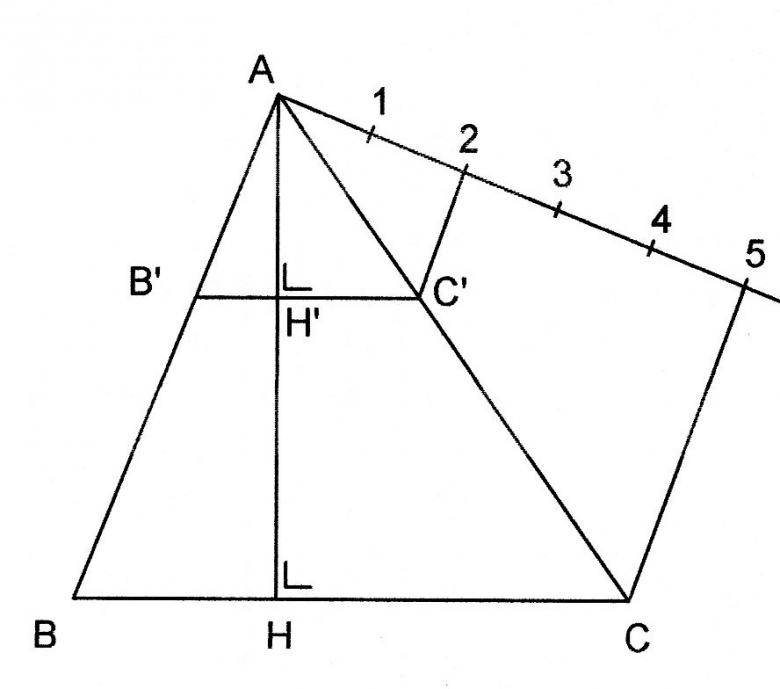
Les triangles ABC et AB'C' sont semblables
Calculez les rapports suivants : AH'/AH et HH'/AH
AH'/AH = 2/5 car la hauteur AH a été réduite dans le même rapport que les c^tés.
Par contre , je ne suis pas sûre pour H'H/AH serait 3/5 mais cela ne me semble pas bon
Pour la question suivante:
Aire du triangle AB'C' = (2/5)² = 4/25
Aire du triangle ABC
Aire du triangle AHC = (5/2)² = 25/4
Aire du triangle AH'C'
j'ai aussi:
aire du trapèze B'C'CB
aire du triangle ABC
cela me semble impossible??? est-ce une erreur dans l'énoncé?
merci
Mamie
Re
là l'astuce est juste de faire des différences de fractions
AH/AH = 1 = (AH' + HH')/AH = AH'/AH + HH'/AH = 2/5 + HH'/AH
et donc HH'/AH = 1 - 2/5 = 3/5, tout à fait
tu fais pareil avec les aires
ABC/ABC = 1 = (AB'C' + B'C'CB)/ABC = AB'C'/ABC + B'C'CB/ABC
et donc le rapport B'C'CB/ABC cherché
?? aucun rapport avec ce que j'ai écrit !!
3/5 n'a pas son mot à dire là dedans et encore moins avec une addition qui ne rime à rien
1 = (2/5)² + (aireB'C'CB / aireABC)
(aireB'C'CB / aireABC) = 1 - (2/5)² = 1 - 4/25 = ?
oui
d'ailleurs on peut vérifier ce genre de choses avec Geogebra par exemple (bien pratique pour vérifier ses calculs)
tu construis ta figure avec Geogebra sans te préoccuper d'aucun calcul que ce soit
tu crées le triangle ABC (polygone) et le quadrilatère B'C'BC
leurs "valeurs" ce sont leurs aires
tu fais calculer le rapport direct de ces valeurs et ... ça doit donner 0.84 (21/25)
cette façon de faire c'est bien sûr juste pour vérifier ses calculs...
tu ne peux pas prétendre : "Geogebra m'a dit que c'est 0.84" sans faire et exhiber les vrais calculs 


