Triangle en bâtons

 Niveau exercicesPartager :
			        
Triangle en bâtons
Posté par 
Imod  26-01-26 à 11:05
Bonjour à tous 

Un exercice très simple et très amusant si on ne triche pas , c'est à dire si on n'utilise aucune machinerie et sans tâtonnements . En bref on ne participe pas si on a  utilisé un programme , une calculatrice , un tableur ou un chat péteur .

On veut construire un triangle équilatéral avec n bâtons de tailles 1 , 2 , 3 , … , n . Tous les bâtons doivent être utilisés et chaque côté du triangle doit comporter un nombre différent de bâtons . Quelle est la valeur minimale de n pour laquelle la réalisation est possible ?

 Exemple de solution refusée : j'ai trouvé ... et il est évident qu'on ne peut pas le faire avec moins de bâtons .

L'exercice est de niveau lycée .

On blanke pour laisser chacun s'amuser 

Imod

 Posté par 
jandri re : Triangle en bâtons  26-01-26 à 11:33
Bonjour,

c'est amusant et c'est du niveau collège (et même école primaire).

Je  trouve comme valeur minimale de n :
 Cliquez pour afficher

n=9 avec sur les côtés 9+6 = 8+5+2 = 7+4+3+1

Démonstration du minimum : Cliquez pour afficher

A partir de n=6 on ne peut pas avoir une seul bâton sur un côté (car 1+2+3+...+(n-2)+(n-1) est plus grand que 2 fois n) donc il y a au moins 2+3+4=9 bâtons et la plus petite valeur de n à examiner est n=9. Or elle convient.

Sans la condition "chaque côté du triangle doit comporter un nombre différent de bâtons" la plus petite valeur de n est  Cliquez pour afficher

n=5 avec 5 = 4+1 = 3+2

 Posté par 
Imodre : Triangle en bâtons  26-01-26 à 11:49
C'est ça Jandri  

C'est pour la justification du minimum que j'ai parlé de niveau lycée .

Imod
 Posté par 
sanantonio312re : Triangle en bâtons  26-01-26 à 11:54
Bonjour,

Le nombre de batons des différents côtés sont différents donc:
 Cliquez pour afficher
Il faut au moins 6 batons. par conséquent n>=3

Le triangle est équilatéral donc Cliquez pour afficher
le nombre total de batons est multiple de 3 et par conséquent n est multiple de 3

 Cliquez pour afficher
Pour n=3 on peut conclure à l'impossibilité sans démonstration

Pour n=6, on a 1, 2 et 3 bâtons pour des côtés de 7 soit:

1 baton: 7 

2 batons: 1+6 ou 2+5 ou 3+4

3 batons: 1+2+4 seule possibilité incompatible avec les autres.

Pour n=9, les côtés mesurent 15

Je vais chercher s'il y a des solutions... 

A tout à l'heure

 Posté par 
jandri re : Triangle en bâtons  26-01-26 à 12:05
La justification du minimum se fait en restant au niveau de l'école primaire en procédant ainsi :
 Cliquez pour afficher
on essaie pour les valeurs successives de n : 3, 4, 5, ...

 Posté par 
dpire : Triangle en bâtons  26-01-26 à 16:57
Bonjour,

 Cliquez pour afficher
La définition donne une configuration minimale de 6 bâtons  1;2;3

soit des nombres de 1 à 6 qui ne donnent aucune solution.

En testant tous les cas débutant par 1 on ne trouve aucune solution

Alors testons par 2 , exemple   2;3;4 soit les nombres de 1 à  9 et un total de 9x10/2 =45  soit 15 par coté.

On tombe sur 8+7; 4+5+6; 1+2+3+9

Je ne pense pas faire mieux...
 Posté par 
sanantonio312re : Triangle en bâtons  26-01-26 à 17:19
 Cliquez pour afficher
Pour n=9, les sommes qui donnent 15 sont:

9+6

9+5+1

9+4+2

9+3+2+1

8+7

8+6+1

8+5+2

8+4+3

8+4+2+1

7+6+2

7+5+3

7+5+2+1

7+4+3+1

6+5+4

5+4+3+2+1

Avec 1+2+3+4+5, seuls 7+8 et 5+9 font le complément mais ont 2 batons.

Il faut donc chercher des côtés à 2, 3 et 4 batons

Avec 1+3+4+7 on peut associer 2+5+8 et 6+9

Avec 1+2+4+8 on peut associer 3+5+7 et 6+9

Avec 1+2+3+9 on peut associer 4+5+6 et 7+8

Réponse finale: n=9 
 Posté par 
Imodre : Triangle en bâtons  26-01-26 à 18:44
Bravo à tous 

En soi l'exercice n'a rien de particulièrement original et il n'est pas difficile mais il y a de nombreuses façons de l'aborder comme le montrent vos réponses .

Je donne la mienne en blanké au cas où certains chercheraient encore 

 Cliquez pour afficher
Il faut au moins n = 1 + 2 + 3 = 6 bâtons pour que le nombre de bâtons soit distinct sur chaque côté . Le côté du triangle vaut n(n+1)/6 , il est donc strictement supérieur à n ce qui entraîne qu'aucun côté ne peut être constitué d'un seul bâton . Il faut donc au moins 2 + 3 + 4 = 9 bâtons . Avec 9 bâtons le côté du triangle doit faire 90/6 = 15 . Sans aucune imagination , on doit choisir entre 9+6 ou 8+7 pour le côté constitué de deux bâtons . On choisit celui que l'on préfère , dans le reste on en prend trois dont la somme fait 15 et le reste coule de source .

Merci à tous pour la participation 

Imod
 Posté par 
dpire : Triangle en bâtons  27-01-26 à 08:44
Bonjour,

Comme l'exercice set fini,je résume 

Le cas 1+2+3 s'élimine rapidement:

En effet ,si il y a 6 bâtons de 1 à 6 ,le total est 6x7/2 = 21 qui impose 7 par coté ; comme 7>6 ,on passe.

Le cas  2+3+4 --->9 bâtons --->total =9x10/2=45  qui donne 15 par coté.

15 = 6+9 ou 8+7

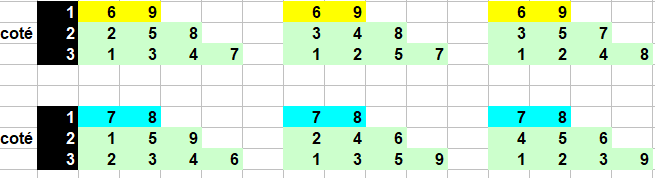
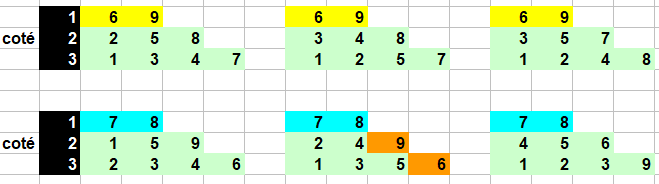
il y a donc 2 solutions: 6+9; 1+3+4+7 ;2+5+8 et 8+7;1+2+3+9; 4+5+6
 Posté par 
Imodre : Triangle en bâtons  27-01-26 à 09:35
En fait il y a 6 solutions car pour chaque choix du côté à 2 bâtons il y a trois possibilités pour le côté à 3 bâtons .

Imod
 Posté par 
dpire : Triangle en bâtons  27-01-26 à 10:46
Pour mois avec n=9--->coté 15   ne me donne pour le coté à 2 bâtons que 6+9 ou 7+8.

Pourrais-tu nous donner les 4 autres solutions ?
 Posté par 
Imodre : Triangle en bâtons  27-01-26 à 10:55
Il faut que tu sois plus clair dans tes questions et tes réponses 

Si la question est de trouver le nombre minimum de bâtons la réponse est unique : n=9 .

Si la question est de trouver le nombre de façons de réaliser les  côtés avec les bâtons la réponse est 6 .

Je te laisse chercher , tu vas trouver .

Imod
 Posté par 
dpire : Triangle en bâtons  27-01-26 à 13:58
OUI

Une fois posé le cas du coté à 2 bâtons ,on peut disposer le coté à 3 bâtons de 3 façons différentes le coté à 4 en résulte.

il y a donc 4 solutions supplémentaires.

Pour  confirmer les 6 solutions pour le triangle équilatéral:

 Cliquez pour afficher
  Posté par 
dpire : Triangle en bâtons  27-01-26 à 14:04
Une petite inversion....

 Cliquez pour afficher