Inscription / Connexion Nouveau Sujet
Triangles semblables. Merci pour votre aide
Je bloque sur deux exercice de géométrie sur les triangles semblables et un calcul d'aire. Merci de votre aide.
1) ABC est un triangle et C est le cercle circonscrit à ce triangle. La bissectrice de l'angle BAC coupe [BC] en D et le cercle C en I
a) Démontrer que ABD et AIC sont semblables.
b) En déduire que AB multiplié par AC = AD multiplié par AI
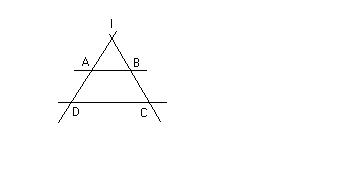
2) ABCD est un trapèze de hauteur 3 cm tel que AB = 6 cm et DC = 4 cm. (AD) et (BC) se coupent en I.
Calculer en cm² l'aire du triangle DIC.
Merci d'avance pour votre aide.
Salut julien 
Pour la première question, il va falloir démontrer que ces triangles ont deux angles de même mesure (en fait trois angles, mais si on en a deux, nécessairement les troisièmes auront même mesure... si tu ne vois pas pourquoi, n'hésite pas à demander  )
)
-------
Bon, déjà, la bissectrice de étant la droite (AD) , on en déduit que
=
Et donc
-------
Ensuite, en remarquant que =
est un angle qui intercepte l'arc
...
bon, je crois que j'en ai trop dit là 
Emma 
quelqu'un aurait t'il une idée pour le second exercice ?
Merci d'avance
Bonjour,
As-tu essayé Thalès??
Bonjour,
tu inverses les lettres du trapèze de Slybar en plaçant AB comme grande base car AB=6 et DC=4.
Comme il te le dit , tu as une confuguration de Thalès dans les 2 tr IDC et IAB.
Tu appelles K le point ou IH (hauteur issue de I dans tr IAB) coupe DC.
Avec Thalès donc : DC/AB=IK/IH=4/6=2/3
Donc IK=(2/3)IH=(2/3)(IK+KH)
Mais KH=3
Tu peux donc trouver IK (=6 sauf erreur) et ensuite l'aire du tr. IDC dont tu connais base=4 et hauteur=6.
Salut.


