Inscription / Connexion Nouveau Sujet
Trigonométrie
 Ramanujan
RamanujanBonsoir,
Soit
Je comprends rien à comment obtenir ces égalités  Pourtant je viens de revoir et redémontrer toutes les formules de trigonométrie mais là je vois pas du tout.
Pourtant je viens de revoir et redémontrer toutes les formules de trigonométrie mais là je vois pas du tout.
Et je comprend pas très bien on te demande de démontrer que D est égale au deux égalité en dessous??/***citation inutile supprimée***
***citation inutile supprimée***
C'est la correction mais j'ai rien compris. L'énoncé est :
Montrer que
Bonjour,
Il manque un - à la première ligne :
D = sin(2x) - sin(4x) + sin(6x) = - 2 sin(x) cos(3x) + sin(6x)
bonjour Sylvieg 
ceci étant dit
rien qu'à la lecture de la 1re égalité, il est évident qu'on ne touche pas à sin(6x) et qu'on utilise sinp-sinq pour le reste
rien qu'à lire la 2e ligne il est évident qu'on utilise sin2a=2sinacosa
....
Ah d'accord merci ! Je n'y arrivais pas car je voulais utiliser la formule dès la première ligne et que dans mon livre il n'y avait pas la formule :
Comment on retrouve cette dernière formule ?
si tu prends le cheminement de cette fiche pour les formules de trigo (au niveau 1re/terminale donc)
![]() Savoir utiliser le cercle trigonométrique et formules de trigonométrie
Savoir utiliser le cercle trigonométrique et formules de trigonométrie
une fois qu'on est là
on pose p=a+b et q=a-b
et on en déduit ce que tu cherches
où est le temps où nos élèves savaient retrouver toutes ces formules en quelques minutes...ils savaient très bien écrire les quelques formules utiles pour arriver là où on désirait arriver....
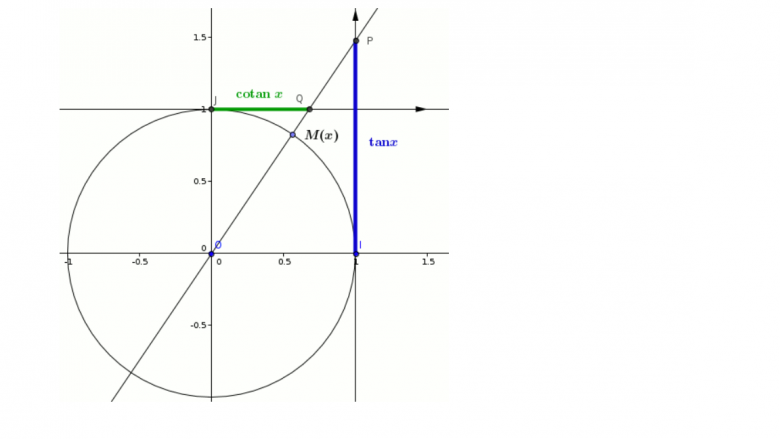
Ah merci la fiche est très bien par contre je comprends pas comment utiliser le cercle pour la tangente.
Comment utiliser le cercle pour retrouver
Oui mais du coup on le retrouve pas sur le cercle directement faut faire :
sin / cos
Sur le cercle on voit que et
D'où le résultat mais c'est pas direct sur le cercle ?
ben si qu'on retrouve ça directement sur le cercle trigo
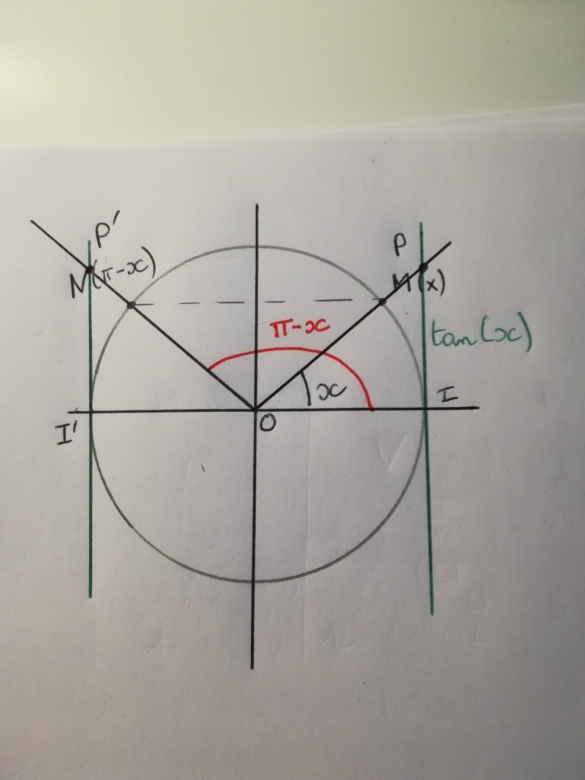
tu positionnes x et pi-x
et tu lis les tangentes !
c'est que tu n'as pas compris cette représentation
tu places sur le cercle N(pi-x)
tu traces (NO) que tu prolonges
elle coupe l'axe vertical passant par I en P'
tu as mesure de IP' qui l'opposée de la mesure de IP
C'est quoi le cercle N(pi-x) ?
J'ai placé le point symétrique de
par rapport à l'ordonnée.
Mais je comprends pas le N(pi-x)
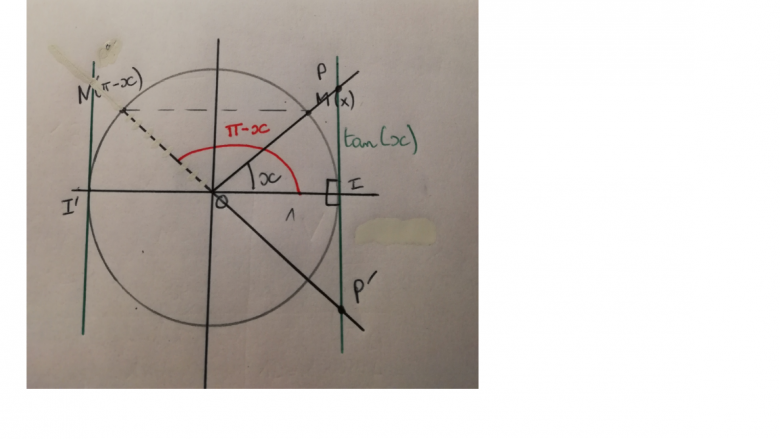
tu traces (NO) que tu prolonges
elle coupe l'axe vertical passant par I en P'
tu as mesure de IP' qui l'opposée de la mesure de IP
elle coupe l'axe vertical passant par I
J'ai corrigé mais je vois toujours pas comment exprimer en fonction de
Dans le triangle rectangle en I , on a pas l'angle
Tu as déjà vu un triangle rectangle avec un angle de mesure comprise entre  /2 et
/2 et  ???
???
Les triangles rectangles, c'est bon pour les angles de mesure comprise entre 0 et  /2 , c'est à dire avec un cosinus et un sinus positifs.
/2 , c'est à dire avec un cosinus et un sinus positifs.
Revoir les définitions de cosinus, sinus et tangente pour t réel quelconque (avec cosinus non nul pour tangente).
Je comprends rien 
C'est quoi le rapport entre et
? Vous utilisez quel triangle pour la trouver ?
J'ai pas compris le but de la construction du point
Comment utiliser la règle tangente = opposé / adjacent si est plus grand que
?
On ne l'utilise pas !
Revoir les définitions de cosinus, sinus et tangente pour t réel quelconque (avec cosinus non nul pour tangente).
Voir cours de seconde.
Bonjour
faudrait peut-être quitter le collège et (re)voir les cours de seconde, là ! l'enroulement de la droite réelle sur le cercle trigo, toussa ...
Bonjour,
Ramanujan es-tu parvenu à démontrer ton égalité du 12-01-19 à 04:55?
Pas encore mais j'essaie déjà de comprendre la tangente sur le cercle.
ce dernier cours t'explique l'introduction de la notion de sinus et de cosinus, indépendamment de tout triangle rectangle
cela fait, on introduit la fonction tangente comme quotient des deux.
Je sais la démontrer par calcul mais j'ai pas compris la méthode graphique.
Je sais que et je sais le démontrer en utilisant sur le cercle les valeurs de
et de
Mais c'est quoi le rapport avec la construction que vous m'avez montré du point ?
mais as-tu su démontrer que représente tan(x) ?
si oui, un coup d'angle opposé par le sommet et tu te ramènes à
ne pas oublier qu'on est sur un axe !
@Pirho j'ai réussi à démontrer l'égalité compliquée. C'est juste des formules de trigo à appliquer.
Comme le triangle est rectangle en
car
Je vois pas comment faire pour et quoi le lien avec le
Bonjour,
Nous ne sommes plus au collège ; donc on abandonne le triangle rectangle...
Avec a réel quelconque, définition de cos a et sin a :
Les coordonnées du point M , où M est le point qui représente la mesure d'angle a sur le cercle trigonométrique de centre O et d'origine A .
Bref M(cos a ; sin a) dans le repère orthonormal direct
La droite (OM) a alors pour équation x sin a - y cos a = 0.
Si cos a  0 , l'équation peut s'écrire y = ...
0 , l'équation peut s'écrire y = ...
La tangente (T) en A au cercle a pour équation ...
Tu en déduis les coordonnées du point P intersection de la tangente (T) avec la droite (OM) .
Ah oui c'est évident si l'équation de la droite est
Un coefficient directeur est
On obtient si que
L'équation de la tangente au cercle en A est
J'obtiens
Mais c'est quoi le rapport avec le qu'on voulait déterminer sur le cercle ?
dans le contexte de ce que tu viens de faire
appelle le plutôt tan(pi - a)
intersection de deux droites dont l'une a pour équation x=1
Ah d'accord donc j'introduis :
La droite a pour équation :
Intersecté avec la droite d'équation j'obtiens :
C'est ça ?
Ah oui c'est évident si l'équation de la droite est
Un coefficient directeur est
ce n'est pas un coefficient directeur, mais le coefficient directeur
mais ici, ce n'est pas le coefficient directeur mais un vecteur directeur qui a pour coordonnées.....
OK pour la suite à condition de donner le lien entre M' et le (pi-a)
D'après mon cours et la représentation paramétrique du cercle unité :
Et après je sais pas quoi faire