Inscription / Connexion Nouveau Sujet
Trigonométrie (seconde)
Bonjour
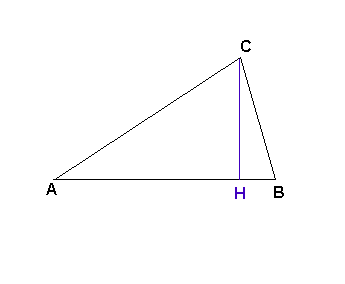
1) ABC est un triangle quelconque [CH] est sa hauteur issue de C. Un utilisant la trigonométrie dans le triangle ACH, démontrer que l'aire du triangle ABC est Aire(ABC) = 1/2 AB x AC x sin BAC. Proposer deux autres formules analogues permettant de calculer la même aire.
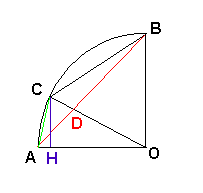
2) On considère un quart de cercle AB de centre O dont le rayon est pris pour unité de mesure. C'est le point de cet arc tel que le triangle OBC soit équilatéral. Les segments [AB] et [OC] sont sécants en D. Faire un schéma.
a) Construire le point H projeté orthogonal de C sur [OA]. Calculer les distances OH et CH, puis démontrer l'égalité AC = V2 -V3 (La racine va sur 2 et racine de 3).
b) Déterminer les mesures en radians des angles BAC et ABC.
C) En utilisant la formule (1), démontrer que l'aire du triangle ABC est Aire(ABC) = V2 x V2 -V3 (La racine va sur 2 et racine de 3) / 4
d) En utilisant l'une des deux autres formules analogues démontrer que sin ABC = V2 -V3 (La racine va sur 2 et racine de 3) / 2
A l'aide de la calculatrice en donner une valeur approchée arrondie à trois décimales. Vérifier cette valeur approchée en utilisant la mesure en radians de l'angle ABC
Pouvez-vous m'aider, SVP merci
Dieu sait que je m'y suis penchée, mais vraiment je n'y comprend rien. C'est trop loin pour moi ce genre de problème
Stella
1)
Dans le triangle rectangle ACH, on a:
CH = AC.sin(BAC)
Aire(ABC) = (1/2).AB.CH
Aire(ABC) = (1/2).AB.AC.sin(BAC)
---
Par une méthode analogue mas en partant alors des hauteurs issues de A et B, on trouve:
Aire(ABC) = (1/2).AC.CB.sin(ACB)
et
Aire(ABC) = (1/2).AB.BC.sin(ABC)
-----
Sauf distraction. 
2)
a)
Angle(BOC) = 60° (puisque le triangle ABC est équilatéral).
-> angle(AOC) = 30°
OC = OB = 1 (puisque le triangle ABC est équilatéral).
Dans le triangle rectangle OHC:
OH = OC.cos(AOC)
OH = 1.(V3)/2 (avec V pour racine carrée)
OH = (V3)/2
CH = OC.sin(AOC)
CH = 1.(1/2)
CH = 1/2
AH = AO - OH
AH = 1 - ((V3)/2)
Dans le triangle rectangle AHC, Pythagore ->
AC² = AH² + CH²
AC² = (1 - ((V3)/2))² + (1/4)
AC² = (1 - V3 + (3/4)) + (1/4)
AC² = 2 - V3
AC = V(2-V3)
---
b)
Dans le triangle rectangle AOB, pythagore:
AB² = OA² + OB²
AB² = 1 + 1 = 2
AB = V2
L'angle au centre (COB) et l'angle (BAC) avec son sommet sur le cercle sous-tendent la même corde BC du cercle.
Comme on a aussi O et A du même coté de la corde BC, on a donc: Angle(BAC) = (1/2) angle(COB)
Angle(BAC) = (1/2) angle(COB) = (1/2).(Pi/3)
Angle(BAC) = Pi/6
L'angle au centre (COA) et l'angle (ABC) avec son sommet sur le cercle sous-tendent la même corde AC du cercle.
Comme on a aussi O et B du même coté de la corde AC, on a donc: Angle(ABC) = (1/2) angle(COA)
Angle(ABC) = (1/2) angle(COA) = (1/2).(Pi/6)
Angle(ABC) = Pi/12
---
c)
Aire(ABC) = (1/2).AB.AC.sin(BAC)
Aire(ABC) = (1/2).V2.V(2-V3).sin(Pi*6)
Aire(ABC) = (1/2).V2.V(2-V3).(1/2)
Aire(ABC) = [V2 .V(2-V3)]/4
---
d)
Aire(ABC) = (1/2).AB.BC.sin(ABC)
[V2 .V(2-V3)]/4 = (1/2).V2.1.sin(ABC)
[V(2-V3)]/2 = sin(ABC)
sin(ABC) = [V(2-V3)]/2
angle(ABC) = arcsin[(V(2-V3))/2] = 0,262 radian.
Or on avait trouvé angle(ABC) = Pi/12 = 0,262 (arrondi à la 3 ème décimale) -> OK.
-----
Sauf distraction.