Si on a le droit aux solutions farfelues, je prends deux cercles passant chacun par le centre de l'autre, je les triple (je crée pour chacun de ces cercles, deux copies identiques superposées), et voilà

Pourquoi pas

Bon maintenant six cercles distincts

Imod

Alors il suffit d'ajouter une dimension :

(je joins une vidéo car c'est beaucoup plus facile à voir en animé qu'en fixe)

chacun des cercles rouges couple le centre des 3 cercles bleus, et vice versa

Bonsoir,
je suis presque certain qu'il n'y a pas de solution avec six cercles de centres distincts.

En fait c'est un problème de combinatoire : il faut répartir  les six centres sur les six cercles.

C'est à dire trouver un ensemble de six parties de {1 ; . . . ; 6} vérifiant chaque partie a trois éléments et elles sont toutes distinctes.

Il n'est pas difficile de trouver un tel ensemble, par exemple :
{{1,2,3} ;  {2,3,4} ; {3,4,5} ;  {4,5,6} ; {5,6,1} ; {6,1,2}}.

Mais quand on regarde les distances entre les centres on voit qu'il y a au moins un cercle qui contient quatre centres.

Bravo Zormuche

Peut-être qu'il est possible d'avoir 6 cercles de centres distincts si on se place en dimension encore plus grande (4, 5, ou 6) puisque les distances sont loin d'être évidentes là-bas

C'était la deuxième étape et maintenant dans un plan
Imod

En dimension supérieure à deux on commence a avoir des problèmes de plans.

L'exercice initial est de niveau collège voire moins , il faut rester simple .
Imod

J'ai triché en allant voir une solution sur internet... je préfère tout de même la mienne dans le plan 3d

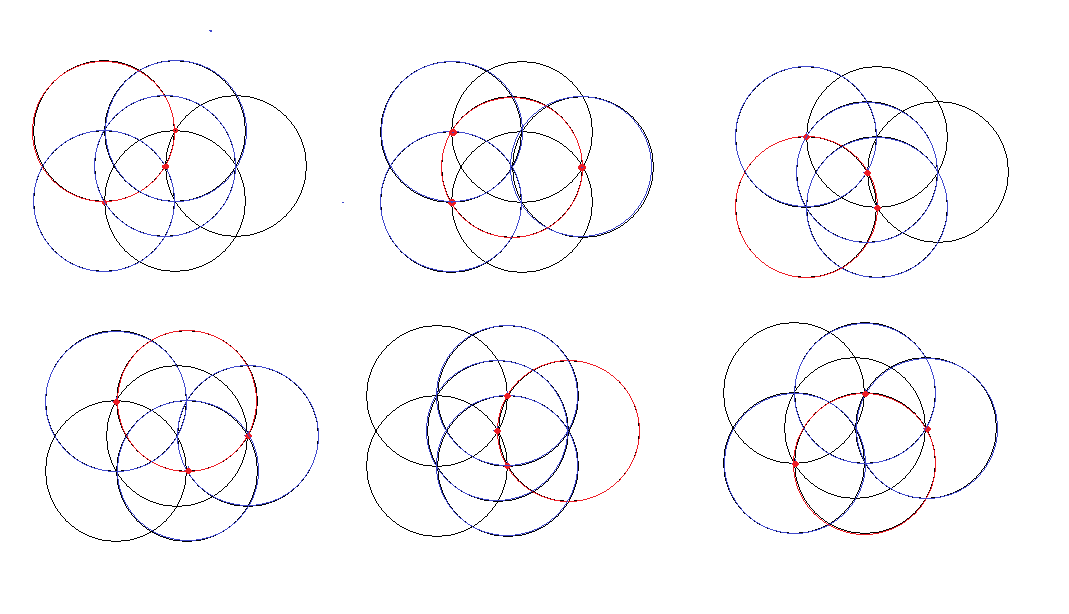
Comme tout le monde semble avoir lâcher l'affaire je donne une solution muette . Chacun pourra retrouver aisément les trois figures élémentaires qui composent la figure

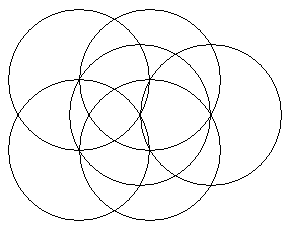
Imod

Semble OK.  

Sur chaque figure :

Le rouge passe par le centre des 3 bleus et ne passe pas par le centre des 2 noirs