Inscription / Connexion Nouveau Sujet
Trouver la hauteur d'un trapèze à partir de son aire
Bonjour à vous,
J'ai un devoir maison pour dans quelques jours où je dois trouver la hauteur d'un trapèze à partir de son aire, seulement voilà, je n'ai pas la longueur de la petite base. Voici l'énoncé :
Soit ABCD un trapèze isocèle. On donne AB = 14 cm, l'angle CBA = 45°, et x la hauteur du trapèze. L'aire totale du trapèze est de 40 cm2.
Calculer la longueur x.
Je sais que la formule de l'aire du trapèze est (B+b)×h/2, sauf qu'il me manque b (petite base CD) et que je dois trouver h (la hauteur x). Je sais juste que la grande base fait 14 cm.
Je remplace avec ce que j'ai : (14+b)×x/2 = 40. J'enlève le dénominateur, donc j'ai (14+b)×x = 80.
Je ne sais pas quoi faire à partir de là, or on sait que l'angle CBA fait 45 °.
Faut-il utiliser la trigonométrie ? J'ai essayé mais sans grands résultats, ou bien faire un système ?
Merci d'avance pour votre aide 
Bonsoir
Un angle de 45 à quoi cela vous fait-il penser ?
Si M est le projeté orthogonal de C sur (AB) que pouvez-vous dire de CMB ?
45° est la moitié de 90, ça je le sais, mais je ne sais pas comment faire après. Et on a pas vu le projeté orthogonal
Bonjour,
le projeté orthogonal c'est le pied de la perpendiculaire
figure cadeau
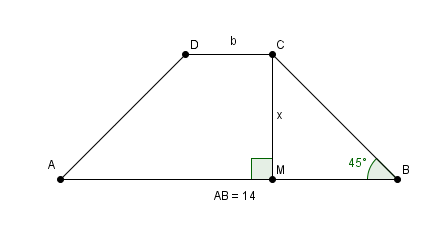
tu parlais de trigo, pourquoi pas, quelle est la valeur de tan(45°) ?
mais ce qui est plus important c'est la nature exacte et complète du triangle CMB ...
la trigo est alors inutile
Bonjour,
Finalement on a réussi à résoudre le problème et à trouver x.
- On a d'abord prolongé les droites (AD) & (CD) pour qu'elles forment un triangle rectangle isocèle.
- Puis on a calculé un des côtés de ce rectangle avec cos(45), on a trouvé me semble-t-il 14×sqrt(2) (je sais pas comment faire la racine sur le site),
- Puis on a utilisé Pythagore pour calculer la hauteur de ce triangle vu qu'on connaît AB et l'un des côtés grâce à cos(45°), on trouve 7 cm.
- On a calculé l'aire totale de ce triangle en faisant (base × hauteur)/2, ça nous donne (14×7)/2=49.
- On sait que ce triangle englobe le trapèze ABCD, on a donc soustrait l'aire du trapèze à l'aire du triangle, ce qui fait 49-40=9 cm2.
- À partir de là, on a pu déduire que la base du petit triangle (c'est le segment [DC]) faisait 6 cm et que sa hauteur faisait 3 cm.
- Or on a vu que la hauteur totale de ce triangle était de 7 cm, donc la hauteur du trapèze = 7-3=4 cm.
- De plus, si on vérifie tout ça, aire du trapèze = ((B+b)×h)/2=((14+6)×4)/2=40 cm2.
Donc voilà problème résolu, merci beaucoup à vous pour m'avoir donné des pistes 
c'est vrai que pourquoi faire simple quand on peut faire compliqué ...
MBC est un triangle rectangle isocèle (question posée et reposée) car angle de 45° donc MB = x
et pareil de l'autre côté
et donc immédiatement b = 14-2x que l'on reporte dans la formule de l'aire du trapèze déja citée etc
ta méthode est certes astucieuse mais (*** edit : à mon avis) rate le but de l'exercice qui était de résoudre l'équation du second degré obtenue
puis de discuter pourquoi une des deux racines est à exclure.
Bonjour à tous
Début d'année de seconde
Je ne suis pas sûre qu'on cherche à les faire passer par du second degré. ..
,)
OK.
n'empêche ma remarque sur " faire compliqué" est justifiée
- Puis on a calculé un des côtés de ce rectangle avec cos(45), on a trouvé me semble-t-il 14×sqrt(2) (je sais pas comment faire la racine sur le site),
- Puis on a utilisé Pythagore pour calculer la hauteur de ce triangle vu qu'on connaît AB et l'un des côtés grâce à cos(45°), on trouve 7 cm
heureusement que l'on trouve 7cm !!
directement sans Pythagore et sans trigo :
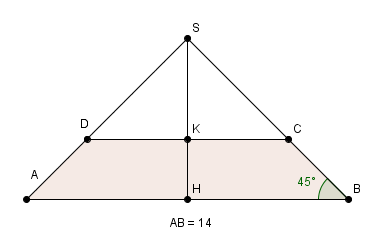
SAB est donc rectangle isocèle (deux angles à la base de 45°)
de même SHB (angle droit et un angle de 45° donc l'autre =180°-90-45 = 45° aussi)
donc SH = HB = AB/2 = 7 cm ...
PS : "heureusement que l'on trouve 7cm" !! après des calculs faux
SB ne mesure pas 14
 2 mais 7
2 mais 7
 2 ou 14/
2 ou 14/ 2
2
et nota :
pour écrire des racines on a les symboles spéciaux de l'ile, cliquer sur Π :



