>Imod
On  peut donc revenir au post d'origine pour 20 km et 5km/h

On a T= (20 x 22)/5 =11,318 h soit  11 h 19 min 13 s

On voit bien que ça marche pour n= 9 et certainement de la même façon pour tous les suivants  .

Pour résumer s'il y a 1 habitant la distance parcourue est , s'il y a 4 habitants elle est de et dans tous les autres cas elle est de . En revenant au problème , ça fait un peu moins que ce que tu annonces , de l'ordre de 11 H 18 min 49 s ( ce qui est quand même déjà très long ) .

J'ai quand même beaucoup de mal à me satisfaire d'un simple on voit bien que . Pourrait-on par exemple prouver que si tous les habitants sont sur la frontière de la commune alors avec plus de quatre habitants la distance ne peut pas dépasser .

C'est sûrement de la pinaillerie car pour moi le problème est résolu

Imod

Nous avons donc déposé la loi imod/dpi  

Encore faudrait-il avoir prouvé quelque chose

J'ai proposé d'envisager le cas où tous les habitants sont sur la frontière , il y a certainement plein d'autres idées , par exemple , pourquoi mettre la maire au centre ?

Imod  

je pense que c'est équivalent au pb du commercial qui doit visiter plusieurs villes ... sauf qu'ici le client devient commercial lui-même ... et évite au commercial primitif de faire le tour de toutes les villes ...

c'est donc aussi un pb de graphe ...

et on doit/devrait donc pouvoir le démontrer proprement ...

Ici le problème est beaucoup plus fermé , il doit y avoir une solution plus simple .

Imod

Je disais plus haut que plus le nombre d'habitants est élevé plus la communication
se transmet.
Supposons tous *
les habitants sur les cotés du carré espacés d'une distance .
Il suffit au maire de faire le parcours 2+2 pour créer 4 flux de 2
*autant qu'il est possible.

hum ! c'est pas tout à fait bon.....

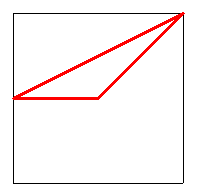
Voilà un des meilleurs parcours pour une infinité de points sur les cotés,
ce qui devrait confirmer la loi

 Cliquez pour afficher

imod/dpi

Il fallait bien que soit dans le coup

Attention , au point (0 ; 1/2) il y a quatre trajectoires pour seulement deux personnages ( la maire et un habitant ) . En plus rien ne garantit que deux milieux de côtés opposées abritent un administré .

Ce n'est pas si simple

Imod

J'ai essayé de justifier la propriété en partant d'un quadrillage qu'on affine à l'infini , mais on tombe  vite sur un problème : la position centrale du maire . Si on supprime cette condition on obtiendrait un parcours maximal de   dans tous les cas sauf s'il n'y a qu'un habitant le maximum étant alors de   .

Ce n'est qu'une idée parmi d'autres

Imod

Bonjour à tous! Pourriez-vous m'éclairer?

Ce que je ne suis pas sûr d'avoir bien compris:

1) Je fixe le nombre d'habitants n à ma convenance.
2) Les opérations sont terminées quand tous les habitants sont rassemblés dans la mairie.
3) Pour une disposition initiale donnée D des habitants dans le carré, je cherche la stratégie qui minimise la durée totale des opérations.
4)Si je note d(D) cette durée minimale, je cherche  D pour que d(D) soit maximale. Autrement dit, je cherche la disposition D la plus défavorable pour n donné.
5)Concernant les règles du jeu:  dès qu'un habitant a été prévenu, il peut démarrer. Il n'est donc pas exclu  que plusieurs d'entre eux marchent en même  temps, côte à côte ou non.
Merci d'avance !

Tu as parfaitement compris le problème .

On ne demande pas forcément d'expliciter la stratégie (  je vois mal comment on peut s'en passer ) mais simplement de donner le temps écoulé entre le départ du maire et l'arrivée de chacun des administrés .

Dpi semble avoir trouvé la règle générale mais il manque une preuve à tout ça  

Je propose de voir ce qui se passe si la maire n'habite plus au centre de la commune mais ( elle aussi ) dans la pire des positions pour rassembler tout le monde .

Imod

Je pense avoir une idée pour avancer un peu

C'est la frontière du carré qui gène bien plus que la position centrale de la maire . Si on considère que les habitants de la commune sont sur un cercle de diamètre 1 et la maire au centre du cercle alors la plus grande longueur est obtenue quand les habitants sont régulièrement espacés .

va tendre vers .

Imod  

J'ai regardé de plus près et même sur cercle c'est très compliqué . Je ne vais pas monologuer éternellement , je regarde encore si une partie du problème est dans mes cordes , sinon je laisse tomber .

Elle est pourtant jolie la conjecture de Dpi

Imod

Bonjour,

Je rentre d'une semaine sans ordi
Avant de partir,j'avais donné les parcours pour un maire en position centrale ayant
tous les habitants sur les cotés du carré en postulant que chaque habitant rencontré
aura trois options,soit suivre le maire soit suivre celui qui l'a renseigné soit aller directement à la mairie si c'est plus court.
j'ai été surpris d'être en dessous de 22,mais mon sens de l'optimisation
m'a poussé à rechercher un compromis entre  1+ et 2+2/2.
En "tournant" à 0.950484 au lieu de 1 on augmente  d'un poil les parcours vert et mauve ,mais on raccourcit mieux les parcours  bleu et orange.

A moins que je n'aie rien compris ( ce n'est pas impossible ) , j'ai l'impression que tu commets toujours la même erreur que j'ai signalée à plusieurs reprises .

Lorsque la maire arrive en (0;1/2) elle transmet le message à une seule personne , donc de (0;1/2) ne peuvent partir que deux personnes or il y en a quatre sur ton dessin

Imod  

Je ne dirai pas cela...
Toujours dans la configuration coloriée...

Le maire fait un parcours qui a pour but de prévenir les habitants ,mais tu as donné la contrainte "un nombre très grand d'habitants sur les frontières  de sa commune".

Bien évidemment  quand il arrive au bord il rencontre 1 habitant qui a bien sûr un voisin ,ils  décident , lui  de  partir en diagonale (parcours mauve) et l'autre de longer les bords (parcours bleu) .

A ce même bord  le maire rencontre un habitant voisin à droite (parcours orange )  qui conseille à son propre voisin de  partir en diagonale ( parcours vert) pendant qu'il longe la frontière (parcours orange).
Un nombre important réduit à la distance entre habitants .
Donc nos  3 premiers points sont tangents.
A noter que si les distances étaient plus significative, le maire ferait un crochet ,mais cela on l'a déjà vu pour 8 ou pour 9..........,

Non , décidément je ne comprends pas ce graphique

S'il y a beaucoup d'habitants sur la frontière du carré alors la maire se dirige aux alentours de (0;1/2) où se trouve un grand nombre d'habitations . Alors les personnes prévenues se dispersent dans toutes les directions puis retour au centre . Le plus grand parcours est de   . C'est inférieur à mais c'est normal , on calcule autre chose .

Imod

Comme ce maxi est inférieur au mien ,tu serais aimable de me le montrer.
On admet tous les deux que la densité  permet de dire que les habitations se touchent..

Le voilà , et s'il ne te convient pas , il faut que tu dises pourquoi ?

Imod

>imod

C'est  à mon tour de ne plus comprendre:
Qui va prévenir a et b ?

Parmi les multiples habitants vivant au voisinage de (0;1/2) , tu en choisi deux nouveaux , un qui va aller en a et l'autre en b ( tout ça en un temps record ) .

Imod  

J'ai enfin compris notre différence de point de vue
De mon coté ,je m'efforçais de prendre des parcours obligatoires qui ne nécessitaient
pas d'autres consignes ,alors que du tien  ,il  faut que chaque habitant ait la consigne
d'aller chercher un cas précis .Bonjour le planning.