Inscription / Connexion Nouveau Sujet
Trouver une distance par la trigonométrie.
Bonjour à toutes et à tous,
J'aurais bien besoin d'un petit coup de main, s'il vous plait, pour arriver à comprendre comment faire pour cet exercice. Voilà :
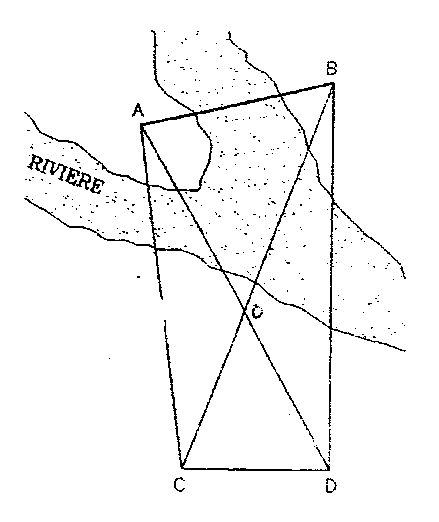
Calculer la distance AB, connaissant :
CD = 450 m
angle ADC = 32 gr
angle ACD = 129 gr
angle BCD = 43 gr
angle BDC = 113 gr
J'avais bien démarré, mais j'ai réalisé que ce n'étaient pas des triangles rectangles, mais des triangles quelconques, et j'ai trop d'inconnues pour utiliser la formule
a² = b² + c² - 2bc cos A
Je vous remercie par avance!
salut
tu peux utiliser la formule
ABC triangle tel que AB=c ;BC=a et AC=b on a
a/sinA=b/sinB=c/sinC
Merci Drioui! J'ai trouvé un ensemble d'équivalences mais je n'arrive pas à voir où ça me mène. Voilà ce que j'ai trouvé :
Triangle ABC : BC/sinA = AC/sin B = AB/0,976
Est-ce qu'il faut que je continue en considérant tous les triangles? Si oui je trouve :
Triangle BCD : 450/sinB = BD/0,625 = CB/0,98
Triangle ACD : AC/0,48 = 450/sinA = DA/0,9
Triangle ABD : AB/0,956 = BD/sinA = AD/sinB
Après je n'arrive pas à continuer... Merci d'avance!
angle(CAD) = 200 - 129 - 32 = 39 gr
CD/sin(CAD) = AD/sin(ACD)
450/sin(39*0,9) = AD/sin(129*0,9)
AD = 702,8 m
AC² = CD² + AD² - 2CD.AD.cos(ADC)
AC² = 450² + 702,8² - 2*450*702,8.cos(32*0,9)
AC = 377 m
angle(CBD) = 200 - 113 - 43 = 44 gr
BC/sin(BDC) = CD/sin(CBD)
BC/sin(113*0,9) = 450/sin(44*0,9)
BC = 691,3 m
AB² = AC² + BC² - 2AC.BC.cos(ACB)
AB² = 377² + 691,3² - 2*377*691,3*cos((129-43)*0,9)
AB = 711,6 m
-----
Calculs à vérifier. 


