Inscription / Connexion Nouveau Sujet
Un lieu en complexes.
Bonjour,
Un topic récent m'a rappelé un exercice:
Trouver l'ensemble des points d'affixes
tels que:
L'exercice est techniquement de niveau Terminale.
Le résultat en soi est une chose; comme souvent, tout est dans la manière.
Comme d'habitude, vous blanquez s'il vous plait 
Bonjour à tous et meilleurs vœux,
alb12 a, comme à son habitude, fait travailler Xcas.
javatasmanie a utilisé adroitement les coordonnées cartésiennes.
Je vous propose une autre solution. Bien entendu, tout le monde peut continuer à chercher sans pour autant regarder les blanqués 
 Cliquez pour afficher
Cliquez pour affichersalut
lake post de 10h36 : pourquoi calculer (z - 1)/(z + 1) ? quel est le lien avec l'énoncé ?
et
posons et
on peut remarquer que :
donc l'ensemble des solutions est symétrique par rapport aux axes du repère et donc leur intersection ... et contient en particulier les complexes -1 et 1 ...
sans le théorème de la médiane (et les notations précédentes) :
Bonjour carpediem,
Je suppose que ceci:
posons
on peut remarquer que :
donc l'ensemble des solutions est symétrique par rapport aux axes du repère et donc leur intersection ... et contient en particulier les complexes -1 et 1 ...
est une tentative d'explication à cela:
Pourquoi calculer (z - 1)/(z + 1) ? quel est le lien avec l'énoncé ?
J'avais vu les choses autrement:
Dès l'instant où on a fait une conjecture quant au lieu (Xcas pour faire plaisir à alb12, méthode différente ou autres...), on conjecture dans la foulée que
Les
sans le théorème de la médiane (et les notations précédentes) :
Là, j'ai carrément du mal à suivre:
Tu as démontré vaillamment que
Et avec

en fait j'ai cliquer sur poster avant de conclure .... ... mais bon je n'arrive pas plus à conclure ... 
mes premières remarques permettaient de conclure à des considérations géométriques du lieu ...
mais ta première réponse donne la solution à "l'équation" AM . BM = 2OM ...

Bonjour,
2 représente le minimum de , c'est-à-dire z réel = 1.
Y-aurait'il d'autres solutions que +/-1?
Alain
Bonjour alainpaul,
D'ordinaire, j'hésite toujours à te répondre; ce n'est pas de la mauvaise volonté, mais je ne comprends pas souvent grand chose.
Ici, je le fais parce que j'ai initié ce topic. Mais je ne comprends encore pas.
Où diable veux tu en venir?

Bon après-midi,
Oui, j'ai relu avec plus d'attention vos réponses:les lieux géométriques (cercles)
donnent les solutions attendues,
Désolé,
Alain
Bonsoir carpediem,
Mais GeoGebra bien sûr! Je suis bien incapable d'en utiliser un autre!
J' ai une équation cartésienne du lieu dépendant du paramètre
En l'occurrence:
Je crée un curseur (ici de 0 à 4)
Je rentre l'équation en question.
Dans les propriétés du curseur, je mets un incrément de 0.2 et je coche la case "Animer"
Dans les propriétés de l'équation, je coche la case "trace"
Et roulez jeunesse 
A noter que les courbes obtenues diffèrent de celles de Robert Ferréol d'une rotation de 90° (ici vu les symétries, un échange de et
)

ha oui d'accord ok !!
tu transformes d'abord en équation cartésienne, ce qui donne un polynome en x et y ... facile à tracer par geogebra.
j'ai la même équation ... mais je ne vois pas comment la transformer plus (de façon simple)
merci 
J'ai cru un moment (en regardant les courbes et comme avec les cercles lorsque ) qu'il y avait une factorisation possible .
Mais après réflexion, je ne crois pas...
J'ai aussi essayé en polaires; on obtient bien quelque chose mais rien de bien réjouissant... 
Bonjour,
A cette occasion j'ai repris un vieux bouquin:"Recueil de problèmes sur la théorie des fonctions complexes" Editions de Moscou de MM Evgrafov et autres.
Il nous donne une construction géométrique de
ainsi que de nombreuses représentations de champs vectoriels à potentiels complexes,
Amicalement,
Alain
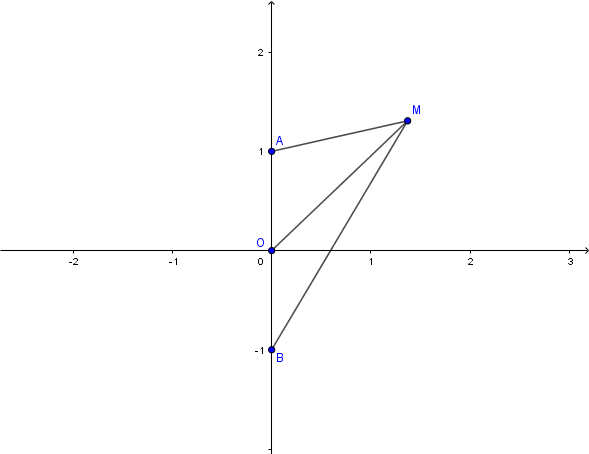
Oui avec et
, il est facile de construire
lorsqu' on connait
:
Un inversion, une symétrie axiale et un milieu de deux points:
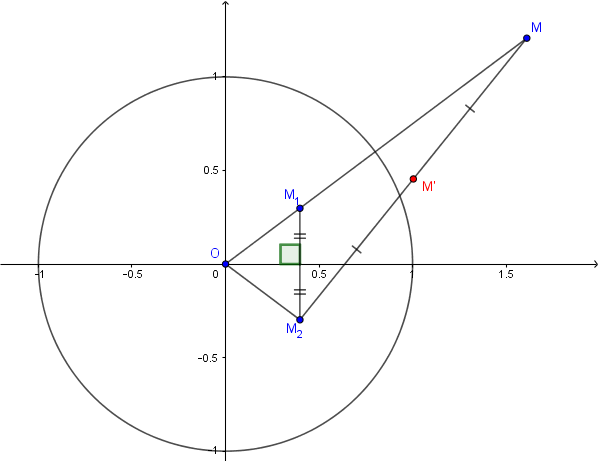
Mais inversement comment construire connaisant
?

a deux antécédents (symétriques par rapport à
) foyers d'une certaine ellipse dont on connait deux diamètres conjugués

est la transformation qui à
d'affixe
non nulle fait correspondre
d'affixe
avec:
, on cherche ses antécédents par
Si est un antécédent,
symétrique de
par rapport à
l'est aussi.
On montre que l'ellipse de foyer et
passant par
admet l'axe des ordonnées pour tangente en
et les diamètres conjugués
et
(ou inscrite dans le parallélogramme
):
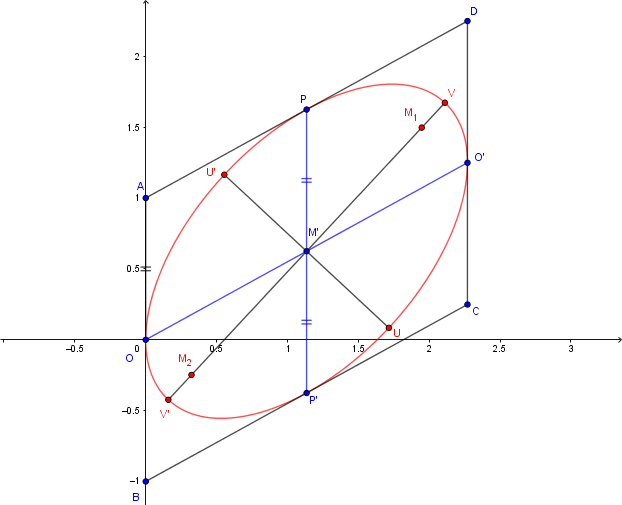
On peut donc construire ses axes puis ses foyers et
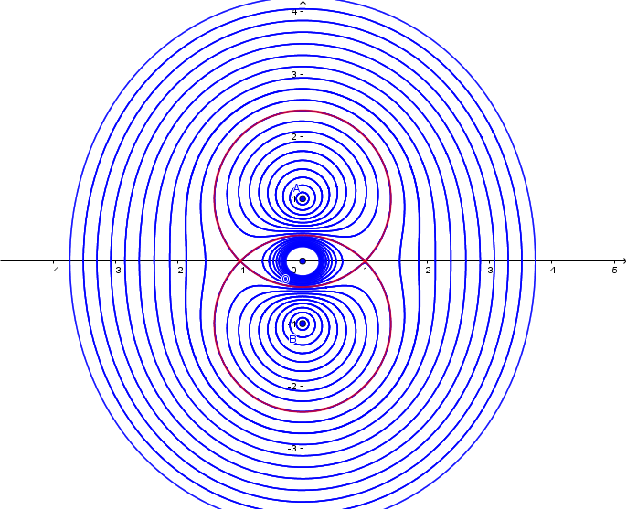
On peut reprendre les lignes de niveau:
avec
On retrouve avec cette méthode les courbes lieux des foyers lorsque décrit des cercles centrés en


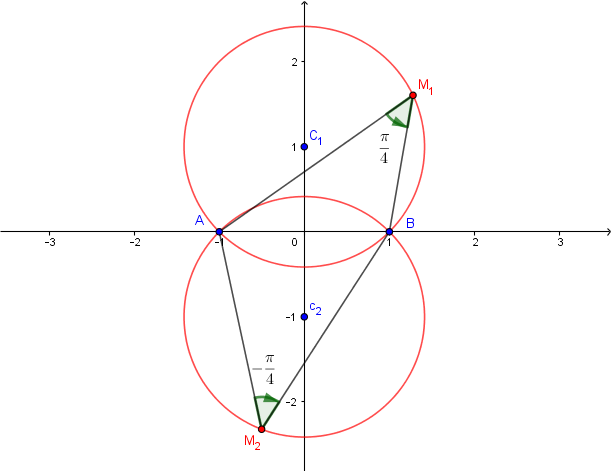

 2,
2,