Bonjour,

Une réponse de simulation numérique :

 Cliquez pour afficher

Il semblerait que ce soit autour de 3.32 étapes en moyenne.
Sauf erreur dans le code bien sûr

 Cliquez pour afficher

#include <stdlib.h>
#include<time.h>
#include <stdio.h>

#define ARR_LEN 8

void shuffle(int * a, int n);
int eliminate(int * a1, int* a2, int n);
int clean(int *a);

int main(){
  srand(time(NULL));
  const int nrun = 1000000;
  double avg = 0;
  for (int i = 0 ; i < nrun ; i++){
    int a1 [] = {1,2,3,4,5,6,7,8};
    int a2 [] = {1,2,3,4,5,6,7,8};
    int nstep = 0;
    int size = ARR_LEN;
    while (size != 0){
      shuffle(a1, size);
      shuffle(a2, size);
      int n = 0;
      do{
	n=eliminate(a1,a2,size);
	size = clean(a1);
	clean(a2);
      }while(n);
      nstep++;
    }
    avg += ((double) nstep)/nrun;
    //printf("Nstep: %d\n",nstep);
  }
  printf("average: %.6f\n", avg);
  return 0;
}

void shuffle(int *a, int n){
  for (int i = 0; i < n - 1; i++) {
    int j = i + rand() / (RAND_MAX / (n - i) + 1);
    int t = a[j];
    a[j] = a[i];
    a[i] = t;
  }
}

int clean(int* a){
  int size = 0;
  for (int i = 0 ; i < ARR_LEN ; i++){
    if (a[i] == 0){
      for (int j = i+1 ; j < ARR_LEN ; j++){
	if (a[j] != 0){
	  a[i] = a[j];
	  a[j] = 0;
	  size++;
	  break;
	}
      }
    }else size++;
  }
  return size;
}

int eliminate(int * a1, int* a2, int n){
  int count = 0;
  for (int i = 0 ; i < n ; i++){
    if ((i > 0) && (a1[i] == a2[i-1])){
      a1[i] = 0;
      a2[i-1] = 0;
      count++;
    }else if (a1[i] == a2[i]){
      a1[i] = 0;
      a2[i] = 0;
      count++;
    }
  }
  return count;
}

On a au moins une estimation du résultat

Une façon de commencer la recherche d'une solution exacte , on part d'une position réduite à n couleurs et on regarde comment la compléter en une position réduite à n+1 couleurs .

Imod

Bonjour,
C'est effectivement un jeu intéressant .
Avec un jeu de tarot,j 'ai pris 8 atouts de 1 à 8 et une couleur de 1 à 8
voici mes scores.
1/ 4 coups
2/4 coups
3/4 coups
4/3 coups
5/3 coups
6)3 coups
7/2 coups
8/3 coups
9/4 coups
10 /4coups
soir une moyenne de 3.4
je vais essayer sur un calcul aléatoire.

Bonsoir,
on peut regarder ce qui se passe quand on a moins de huit couleurs.
Par exemple avec trois couleurs il n'y a qu'une chance sur six pour que la configuration ne soit pas complètement réduite au premier coup.

Oui , c'est l'idée la plus naturelle . Avec 2 couleurs le jeu s'arrête immédiatement et avec 3 couleurs le nombre moyen d'étapes est 6/5 . Une autre idée est de compter les positions réduites avec n couleurs , ce calcul pouvant se faire en brut ou en tenant compte des symétries des couleurs . Par exemple pour 3 couleurs , on peut considérer qu'il n'y a qu'une position réduite . En effet , on positionne les 3 versos blancs une case sur deux avec les rectos 1 , 2 et 3 et il faut disposer les 3 versos noirs dans les espaces à droite des précédents . Si on veut le nombre réel de positions il faut multiplier par 6 X 2 pour tenir compte des couleurs des rectos et des versos . Il semble plutôt naturel de ne compter qu'une position 3,1,2 pour les noirs . D'autre part il est facile de compter le nombre de positions réduites à n+1 couleurs connaissant celui à n couleurs .
Je précise que je n'ai pas de réponse au problème ( j'aime bien chercher avec les autres ) , mes propositions ne sont pas à prendre comme des indices
Imod      

Ce qui surprend c'est le peu de coups pour aboutir...
Avec l'aléatoire pour 8 couleurs je reste entre 3.2 et 3.5
Avec mon jeu de tarot pour 5 couleurs je trouve 1.8 et pour6 , 2.2
Si on fait un tableau de nos expériences on a:
2 couleurs  1 er coup
3 couleurs   1.2 coup
4 couleurs   1.4 coup
5  couleurs  1 .8 c oup
6estimation   2.2
7estimation   2.7
8 couleurs  3.4 coups

Personnellement j'ai commencé avec des pions de sudoku rouges et noirs ( cadeau de ma petite fille ) . La première question à se poser : pour un nombre de couleurs donné , combien existe-t-il de positions réduites ? On positionne les pions noirs 1 , 2 , 3  , ... et on regarde comment placer les blancs . Je ne vois pas comment progresser sans répondre à cette question . L'écrasement du nombre de jetons est assez rapide au début mais il me semble que ça ralentit assez vite .



Imod

Quelque chose qui correspond "curieusement" à c(n;2 )/n

Sous les conditions que j'ai proposées le nombre de positions réduites pour 1,2,3,4 et 5 couleurs est : 0,0,1,3,15, ... Il faudrait voir plus loin pour trouver une formule

Imod

Bonsoir,

Ça ne répond pas à la question, mais voici le nombre de coups nécessaires en fonction du nombre de couleurs, qui fit bien avec 0.48*n - 0.54 (en supposant que le code que je propose ci-dessus fonctionne).

 Cliquez pour afficher

3 1.199616
4 1.543548
5 1.957542
6 2.401972
7 2.857513
8 3.317788
9 3.787010
10 4.254448
11 4.728221
12 5.213412
13 5.685043
14 6.165067
15 6.646516
16 7.134995
17 7.618095
18 8.097554
19 8.584273
20 9.070318
30 13.970787
40 18.893140
50 23.832071

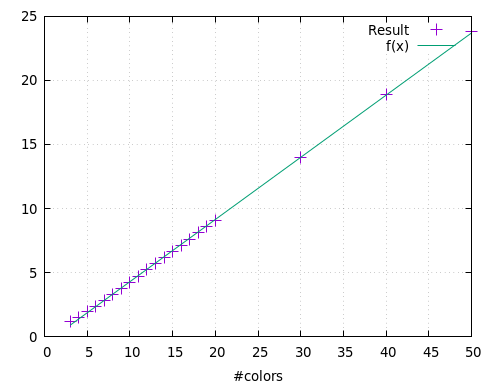
Bonsoir,
avec 3 couleurs on sait qu'il faut exactement 1,2 coup en moyenne pour terminer le jeu.
Avec 4 couleurs il y 3 possibilités
— il reste 4 couleurs : proba 3/24
— il reste 3 couleurs : proba 7/24
— c'est fini : proba 14/24.
On peut donc calculer exactement le nombre moyen de coups pour 4 couleurs.
Mais je trouve un résultat manifestement faux.
Si quelqu'un⋅e veut bien faire le calcul . . .

D'un autre côté j'ai écrit un peu de code pour voir comment se réduisent les dispositions possibles en utilisant la même méthode qu'Imod.
Le code python ( avec quelques bizarreries )

 Cliquez pour afficher

from itertools import permutations

def reduit(liste):
    pasFini=True
    a_supr=[]
    while pasFini:
        pasFini=False
        for i in range(len(liste)-1):
            if liste[i]==liste[i+1]:
                pasFini=True
                a_supr+=[i,i+1]        
        for i in reversed(a_supr):
            del liste[i]
        a_supr=[]
    return len(liste)

def compte_reduc(n_couleur):
    compte=[0]*(n_couleur+1)
    for p in permutations(range(n_couleur)):
        a=zip(range(n_couleur),p)
        l=[t for t in a]
        ll=[]
        for t in l:
            ll.extend(t)
        compte[reduit(ll)//2]+=1
    return compte

Je suis d'accord avec ton étude .
En utilisant mes résultats pratiques et mon observation du 14 /04 à 17h42 ,on voit qu'il y certainement une formule à trouver.

Chacun suit son chemin , on se retrouvera à la fin

Une autre façon de compter le nombre de positions réduites avec n couleurs interchangeables . Ce n'est rien d'autre que le nombre de permutations f de [[1,n]] telles que f(k) n'est jamais égal à k ni à k+1 . C'est comme des dérangements avec une condition en plus .

Imod

Un petit coup d'œil à l'OEIS m'indique que ce calcul est connu sous le nom du problème des ménages où on sépare les couples à une table , il y a deux versions : circulaire ou linéaire . Les formules sont connues dans les deux cas , je vous donne le lien  

Dans le cadre qui nous intéresse le nombre de combinaisons pour un nombre de couleurs inférieur ou égal à 8 : 0 , 0 , 1 , 3 , 16 ,96 ,675 , 5413  . Après il faut voir comment poser les probabilités sur ces résultats .

Imod

Pour 4 couleurs j'ai les mêmes proba que Verdurin qui donnent un nombre d'étape égal à 7/5 . C'est surprenant car pour 2 , 3  et 4 couleurs on a 5/5 , 6/5 et 7/5 pour le nombre d'étapes , sans doute une coïncidence . J'ai commencé à regarder pour 5 couleurs mais c'est un peu long .

Imod

Pour 4 couleurs je trouve une espérance de 54/35.
Mon calcul en notant E₃=6/5 et E₄ les espérances pour 3 et 4 couleurs :
24E₄=1+7E₃+3E₄.

En prolongeant le calcul ( avec un programme ) je trouve pour n couleurs :
n=3  espérance

n=4  espérance

n=5  espérance

n=6  espérance

n=7  espérance

n=8  espérance

n=9  espérance

n=10 espérance

Ce qui correspond bien aux résultats des simulations de thetapinch27.
Je me suis limité à n=10 car j'utilise la force brute et que ma fonction de réduction n'est sans pas optimale.
La fonction python

 Cliquez pour afficher

def liste_esp(n):
    esp=[0,1,1,Fraction(6,5)]
    for k in range(4,n+1):
        s=compte_reduc(k)
        f=sum(s)
        q=f-s.pop() #denominateur
        p=sum([t[0]*t[1] for t in zip(s,esp)])+f
        esp.append(p/q)
    return esp

D'accord , j'ai vu mon erreur pour n=4 .

Je m'agaçais dans mes comptes et recomptes pour n=5 . J'ai fini par trouver : 42 -> 0 ; 35 -> 3 ; 27 -> 4 et 16 -> 5  qui donnent bien l'espérance attendue . Je vais encore regarder les différentes probabilités en fonction du nombre de couleurs pour voir si quelque chose de simple apparait mais j'ai de plus en plus de doutes .

J'ai d'autres idées inspirées du même modèle mais j'attendrai d'y avoir réfléchi un peu plus avant de les proposer .

Il reste tout de même la quasi linéarité des solutions qui pose question . Il faudrait prospecter vers les grandes valeurs de n pour voir si les liens ne se desserrent pas , ça devient vite monstrueux si on navigue sans cap .

Imod

Une remarque oubliée : le nombre de permutations qui se réduisent à en un coup est le nombre de Catalan C_n ( voir ) si il y a n couleurs. C'est évident quand on considère que la première apparition d'une couleur ouvre une parenthèse et que la seconde la ferme.

Je n'avais pas la référence mais c'était mon idée initiale , l'apparition d'une nouvelle couleur sans réduction est extrêmement contraignante . Après il faut voir quoi en faire et là c'est une autre paire de manches

Imod

Un calcul jusqu'à 11.
Sur chaque ligne on a le nombre de couleurs restantes, de 0 à n.
n=3  [5, 0, 0, 1]
n=4  [14, 0, 0, 7, 3]
n=5 [42, 0, 0, 35, 27, 16]
n=6 [132, 0, 0, 154, 162, 176, 96]
n=7 [429, 0, 0, 637, 819, 1232, 1248, 675]
n=8 [1430, 0, 0, 2548, 3780, 7040, 9984, 10125, 5413]
n=9 [4862, 0, 0, 9996, 16524, 35904, 63648, 91125, 92021, 48800]
n=10 [16796, 0, 0, 38760, 69768, 170544, 355680, 641250, 920210, 927200, 488592]
n=11 [58786, 0, 0, 149226, 287793, 772464, 1825824, 3898125, 7085617, 10199200, 10260432, 5379333]
Ça commence à faire un temps de calcul de l'ordre de trois minutes.
Et il augmente comme n!.

Merci pour cette réponse détaillée

Il reste des points d'interrogations qui clairement me dépassent ,  personnellement je laisse reposer ( je fonctionne bêtement comme la pâte à crêpe ) .

Un grand merci à toi ainsi qu'aux autres participants

Je vais proposer un nouveau problème plus simple inspiré de la même idée .

Imod