Inscription / Connexion Nouveau Sujet
Vecteur+trigo
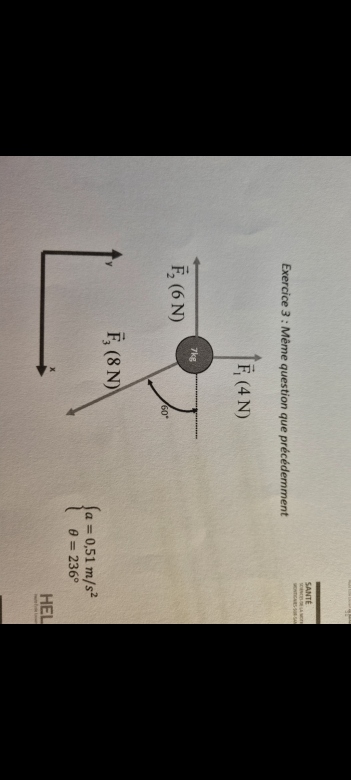
Bonjour serait-il possible de m'aider sur cette question je dois trouver l'accélération de l'objet connaissant les forces qui lui sont appliquées l'objet pèse 7 kg les forces sont décrites sur le schéma.
Selon mon raisonnement j'ai un problème avec les cosinus et les sinus.
J'ai calculé l'axe des x en faisant l'équation - 6 + 8 cos de 60 = 7ax puis j'ai calculé l'axe des Y en faisant 4 + 0 + 8 sin de 30 = 7ay
Chaque résultat que j'ai obtenu je l'ai mis au carré en utilisant le théorème de Pythagore mais je ne retombe pas sur le vrai résultat de l'accélération qui est de 0,51 m par seconde avec un angle de 236 degrés.
Pouvez-vous me dire quel est le hic même si je sais que c'est un raisonnement dans les cosinus mais je ne comprends pas j'ai un peu de mal à comprendre la trigo ^^
Merci beaucoup
salut
en math sup il serait bien :
a/ de faire un aperçu afin de mettre l'image dans le bon sens
b/ de savoir écrire des mathématiques : ce n'est pas "cos de 60" mais cos 60 ° qu'il faut écrire
ce n'est pas sin 30° qu'il faut prendre mais -sin 60 ° = -cos 30 ° pour projeter sur l'axe des ordonnées
et le moins car les forces projetés sur l'axe des ordonnées n'ont pas même direction ...
L'objet n'a pas de poids ? Il est peut-être inclus dans F_1 si c'est un mobile flottant 
Si tu veux procéder par projection sur les axes, le pfd dit que .
Les deux premiers vecteurs ne posent pas de problème ils sont dirigés selon les axes x et y, il faut projeter seulement le troisième.
Le vecteur unitaire correspond à un angle
dans la base (directe)
.
Tu peux donc appliquer le cours et dire que
Et donc
Puis
Et donc
Malou édit > c'est nouveau de faire le travail à la place du demandeur ?


 trigonométrie en post-bac
trigonométrie en post-bac