Calculer une moyenne : Astuce pour les calculs de moyennes

Calculer une moyenne avec coefficients (moyenne pondérée)

Pour faire un calcul de moyenne avec coefficients, il faut multiplier chaque valeur par son coefficient,
puis diviser le total (somme des valeurs) par la somme des coefficients

Exemple :

Jean-Pierre a eu les notes suivantes :

Matière	Coefficient	Note
Mathématiques	4	12/20
Histoire	2	14/20
Français	3	18/20
Sport	2	15/20

Il aura donc reçu 4 notes.
Mais la somme des coefficients est : 4+2+3+2=11

Sa moyenne est donc :

Calculer une moyenne d'âges

Comme pour une moyenne normale (non pondérée ou sans coefficient), on additionne toutes les valeurs et on divise le total (somme des valeurs) par le nombre de valeurs.

Cela revient en fait à une moyenne pondérée où tous les coeffificents sont 1.

Si plusieurs personnes ont le meme âge, on peut utiliser les coefficients, mais dans ce cas là il ne faut pas oublier de compter 1 pour chaque valeur unique afin d'avoir une somme des coefficients cohérente.

Remarque : Un bon moyen de savoir si on a fait une erreur est de voir si la moyenne calculée n'est pas supérieure à la valeur la plus haute prise en compte dans le calcul de moyenne, si c'est le cas, vous avez surement oublié un ou plusieurs coefficients lorsque vous avez divisé la somme des valeurs par celle des coefficients

Exemples :
Dans la famille Dupont, il y a :

Papa	43 ans
Maman	43 ans
Jeanne	12 ans
Pierre	9 ans

Nous avons donc :

Calculer une moyenne sur 10, 20, sur 30, sur 30, etc...

Il existe deux méthodes pour ramener une moyenne d'un dénominateur à un autre : le produit en croix et la méthode de réduction de fractions, ou d'opérations sur les fractions :

Produit en croix :

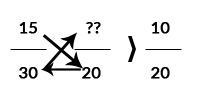
Opération sur les fractions pour arriver sur le dénominateur recherché

Une moyenne est en fait une fraction, par exemple, est égale à ou à . Vous voyez là où on veut en venir ?

Ces manipulations sur les fractions peuvent vous permettre de ramener votre moyenne au dénominateur recherché en passant par des manipulations successives via des dénominateurs plus simples à calculer mentalement, comme 10, 50, etc... selon le dénominateur où vous souhaitez arriver.

Cette méthode offre parfois un avantage par rapport au produit en croix, car il est souvent plus facile de faire ces opérations mentalement qu'en posant un produit en croix, qui demande parfois des multiplications un peu plus compliquées que celles que vous maîtrisez grâce à vos tables de multiplications

Exemples :
- Ramener une note sur 20 à une note sur 10 :



Ici très simple, on divise simplement par 2 le numérateur, et le dénominateur...

- Ramener une note sur 30 à une note sur 20 :



Un peu plus compliqué ici, on peut choisir de diviser par 3 pour arriver à une note sur 10, puis de multiplier par 2 pour arriver à une note sur 20 :



ou alors de multiplier par 2 pour arriver à une note sur 60, pour ensuite diviser par 3 et arriver à une note sur 20 :



- Ramener une note sur 50 à une note sur 20 :



Multiplier par 2 pour arriver à une note sur 100, pour ensuite diviser par 5 et arriver à une note sur 20 :



- Ramener une note sur 100 à une note sur 20 :


On divise par 5 pour arriver à une note sur 20 :