DEFI 181 : Restrictions budgétaires.

Posté par minkus minkus

Bonjour,

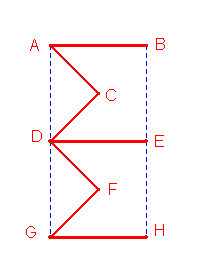
La figure ci-dessous représente le réseau ferré de la ville de Math-City.



Par souci d'économie, le maire décide d'abandonner l'entretien d'un certain nombre de voies.

Deux impératifs doivent être respectés :

*Deux gares quelconques parmi les huit de la ville doivent toujours être reliées, quitte pour le voyageur à emprunter une correspondance.

*Le coût d'entretien, proportionnel à la longueur totale des voies, doit être minimisé.

Quels troncons le maire doit-il supprimer ?

Bonne réflexion.

minkus

Posté par dhalte dhalte

Bonjour,
çà ressemble à la précédente, non ?

Posté par rezoons rezoons

comme il doit toujours avoir 2 gares reliées et qu'il y a 8 gares il faut au minimum 7 troncons donc ma reponse est:

Posté par xtasx xtasx

Bonjour,

Les tronçons les plus courts sont les demi-diagonales et il faut au moins 7 tronçons pour relier les 8 stations.

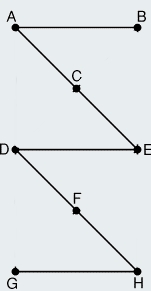
Par exemple le maire peut garder les tronçons AC, BC, CD, CE, DF, FG, FH, soit 7 demi-diagonales. Il supprime donc les tronçons AB, BE, ED, DA, EH, HG, GD, EF.

Posté par Eric1 Eric1

bonjour

Je sgarderais eulement les troncons:
AC,CB,CD,DF,FE,FG,FH

Mais ca sent le piège

Posté par Nofutur2 Nofutur2

AB,AD,BE,DE,DG,GH,EH et DF.

Posté par thomas thomas

ac be dc ad df ef eh gh
je crois ke c'est ca

Posté par kiko21 kiko21

Bonsoir,

Il faut enlever 8 troçons : AB - AD - BE - DE - DG - EH - GH - CE

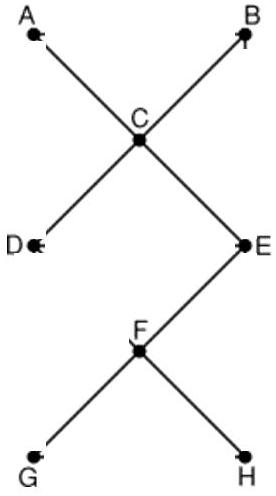
Il reste le réseau suivant en image ressemblant à un Y sur un X




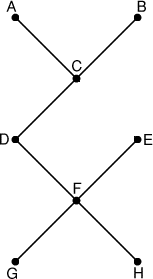
Merci Minkus. A+, KiKo21.

Posté par frenicle frenicle

Bonsoir,

Je propose de supprimer les tronçons AB, DE, GH, AD, DG, BE, EH et DF.

Il restera les 7 tronçons CA, CB, CD, CE, FE, FH et FG.

Cordialement
Frenicle

Posté par plumemeteore plumemeteore

bonjour Minkus
il faut conserver sept tronçons diagonaux : CA CB CD CE DF FG FH
si le coût de AB était 1, le coût total sera 4,95 environ

Posté par Mathieucote Mathieucote

Bonjour
puisque'il y a 8 stations, je dois garder 7 tron¸ons pour que toutes les voies soient liées
je supprime donc les segments :
AB
AD
BE
DC
DE
DG
EH
GH


merci
Mathieu

Posté par master_och master_och

Bonjour

Pour relier 8 points il faut au moins 7 tronçons, donc il suffit d'utiliser 7 tronçons de longueurs minimales (ici  la longueur minimale est égale à la longueur d'un demi diagonale).
ainsi les tronçons à supprimer serons :

AB , BE , DE , AD , EH , GH , DG , DF

et il y'en a d'autres solutions ...

merci pour l'énigme .

Posté par lo5707 lo5707

bonjour,

Il est clair qu'il est préférable d'abandonner des voies verticales et horizontales.
En les enlevant toutes, il reste un voie diagonale en trop.

On abandonne: AB - AD - BE - CE - DE - DG - EH - GH.

_{géométriquement, le réseau a la forme d'un Y sur un X...}

merci pour l'énigme.

Posté par piepalm piepalm

On doit pouvoir supprimer:AB, AD, BE, DE, DG, EH, GH et par exemple EF

Posté par mathématics mathématics

Bonjour,

Voici ma solution :

Posté par mathématics mathématics

Je ne sais pas si l'image est passée alors je la renvois :

Posté par o_0 o_0

Il doit supprimer 8 tronçons: AB, BE, AD, DE, DF, EH, DG, GH et ainsi la longueur totale sera de 4,94 pour c = 1

A                 B
  .             .
       .     .
          C
       .     .
  .             .
D                 E
                .
            .
          F
       .    .
   .            .
G                 H

Posté par Good-Boy Good-Boy

Les tronçons qui suivent, peuvent être enlevés :
AB, AD, BE, CE, DE, DG, EH, et GH

Posté par dami22sui dami22sui

Salut minkus, voila ma reponse:
Je pars du principe que AC=2 et ab=2
Si on ne supprime rien, il y aura 14+82 longueurs
Les troncons a supprimer sont:
AB BE ED DA DG GH HE de toute facon
Apres il faut supprimer un troncon parmi CD, DF, FE, EC.
Il restera 72 longueurs
Il reste 7 troncons, ce qui est le minimum pour relier 8 voies.

Merci du challenge
dami22sui

Posté par gloubi gloubi

Bonjour,

Une possibilité:

suppression des tronçons A-C, A-D, B-E, C-E, D-F, D-G, E-H, F-H.

A+,
gloubi

Posté par zimski zimski

salut a vous tous
ben voila ma solution!
les segements avec des "X" sont a supprimer
les segements avec des ptits rond sont a garder
@+

Posté par Thiamat (invité)

Les troncons qu'il faut continuer d'entretenir sont en bleu et ceux que l'on peut laisser à l'abandon sont en rouge. je pense qu'il s'agit de la solution la plus économique.

Merci

Posté par xmelanie54x xmelanie54x

FH ???

Posté par vince909 vince909

Bonjour,

Personnellement, pour minimiser le coût d'entretien tout en conservant une connectivité entre les gares, je pense que le maire doit faire retirer les tronçons suivants :

A - B
A - D
B - E
D - E
D - F
D - G
E - H
G - H

Il reste donc en place les tronçons suivants :

A - C
B - C
D - C
E - C
E - F
G - F
H - F

Merci pour le défi.

Posté par jacques1313 jacques1313

Je n'ai pas trouvé de meilleure solution qu'en gardant sept tronçons comme dans la figure ci-jointe.
Donc les tronçons que j'ai enlevés sont :
AB, AD, BE, DE, CE, DG, EH et GH.

Posté par evariste evariste

Il supprime :
A-D,A-B,B-E,D-E,D-G,G-H,H-E,F-D

Posté par Judeau Judeau

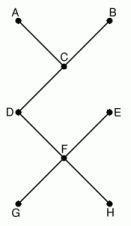
Bonjour,

Le maire doit supprimer tous les tronçons horizontaux et verticaux ainsi que n'importe laquelle des demi-diagonales parmi CD, DF, FE et EC. Ca peut donner un réseau ferroviaire en forme de Y sur un X comme ci-dessous :

Posté par Matthieu_94 Matthieu_94

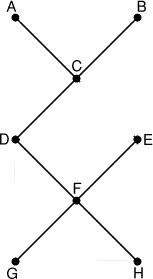
Pour faire des économies, le maire devrai enlever les voies :
ab-be-eh-hg-gd-da-de
bon voila c'est ma première énigme si je me suis trompé quelques part, excusez moi..

Posté par geo3 geo3

Bonjour
Sans approfondir sans doute le tracé en rouge.
A+

Posté par Sigma Sigma

Hi,

Voici ma réponse.

Posté par Flo08 Flo08

Bonjour,

On peut supprimer tous les tronçons les plus longs:
AB, AD, BE, DE, DG, EH et GH.
On pourra ensuite supprimer, au choix, un des tronçons suivants:
CD, CE, DF ou EF (logiquement, le moins utilisé des quatre )

Posté par lapetanque (invité)

il faut enlever les voies AD DG GH EH BE AB DE EF
ainsi pour faire AB A,C,B
                 AC A,C
                 AD A,C,D
                 AE A,C,E
                 AF A,C,D,F
                 AG A,C,D,F,G
                 AH A,C,D,F,H
                
                 BC B,C            CD C,D       DE D,C,E   EF E,C,D,F
                 BD B,C,D          CE C,E       DF D,F     EG E,C,D,F,G
                 BE B,C,E          CF C,D,F     DG D,F,G   EH E,C,D,F,H
                 BF B,C,D,F        CG C,D,F,G   DH D,F,H
                 BG B,C,D,F,G      CH C,D,F,H              FG F,G
                 BH B,C,D,F,H                              FH F,H
                                                          
                 GH G,F,H

Posté par Avangogo Avangogo

Pour relier huit gare, il faut au moins sept voie.
Pour minimiser le cout d'entretien, on ne garde que des petites voies, c'est-à-dire des demi-diagonales des carrés.

On peut donc supprimer:
AB, BE, AD, DE, EH, GH, DG qui sont des vies trop longues
ainsi que CE, qui est inutile.

Un nombre et une longuer des voies minimale, le cout d'entretien est donc bien minimisé.

Posté par ITMETIC ITMETIC

Pour relier 8 gares il faut au minimum 7 tronçons.

Le réseau actuel est composé de 7 tronçons "longs" (horizontaux et verticaux) et de 8 tronçons courts (diagonaux).

Il est possible de relier les 8 ville en ne gardant que 7 tronçons courts, en abandonnant un des 4 tronçons du carré CDEF.

Il y aura donc 4 solutions qui abandonnent les tronçons horizontaux (AB, DE et GF), les 4 tronçons verticaux (AD, BE, DG et EH) et l'un des quatre tronçons parmi DC, CE, EF et FD

Posté par fong fong

bonjour, je propose:
qu'on peut supprimer les voies ab, ad,dg, gh, he, eb,de et df

Posté par bobgui12 (invité)

Ma réponse:
A-B
A-D
B-E
C-E
D-E
E-H
F-H
G-H

Posté par bebedoc (invité)

afin d'éliminer un maximum de route il faut ne garder que les deux diagonale du carré du haut une diagonale du carré du bas et le dernier point du carré du bas est relié par un demi diagonale ceci nous fait éliminer 7 + cotés
c'est le maximum éliminable

donc on retire : AB BE EH HG GD DA (le "tour") et DE  et par exemple FE

Posté par balhou (invité)

Je pense que le maire devra supprimer les tronçons AD AC CE DF FG et EH si il veut que toutes les agres soient reliées .

Posté par amélie13 (invité)

tronçons à enlever : AD , AB , BE , DE , EH , GH , DG

Posté par magali850 (invité)

DE

Posté par minkus minkus

Bonjour,



Cette phrase de Judeau résume bien le problème.

Intéressant de voir les réponses successives de geo3 et sigma.

minkus

Posté par Matthieu_94 Matthieu_94

Heu... j'ai eu faut et on m'a tout de même compté juste.. :s
C'est que je suis bon joueur

Posté par Mathieucote Mathieucote

ouais j'avoue, mais je ne pense pas que minkus va vraiment t'enlever ton smiley...
par contre tu as la même réponse que amélie13, qui a eut un poisson, alors je sais pas trop, nous verrons...