ENIGMA 24: Toujours avec la bicyclette ...

Posté par monrow monrow

Bonjour !

Ici, on va essayer de faire une petite généralisation de l'Enigma 23 .

Ici, on dispose de n amis, et qui sont toujours dans la même situation : Ils n'ont qu'une bicyclette qui roule à 50km/h, outre leurs pieds qui leur permettent de marcher à 5km/h et cela pour atteindre une ville qui se situe à 60km de leur village pour un rendez vous.

Peuvent-ils arriver à la ville en moins de n heures?

Si vous remarquez qu'il y a des données manquantes, répondez : Problème impossible !

Une démonstration est bien obligatoire pour avoir son !

Bon courage

Posté par Nofutur2 Nofutur2

On suppose que les n amis arrivent en même temps, ce qui optimise le trajet.
Pour que le trajet soit optimal, il faut qu'il soit symétrique, donc que A1 parte avec A2 en moto, le dépose à une distance L de l'arrivée et retourne chercher A3 qui est parti à pied, et fasse des allers retours jusqu'à ce qu'il aille chercher An et en plus que le point de rencontre soit à L du début.
Les n amis partent et arrivent en même temps, et en plus, le temps pendant lequel A2, A3, A4….An marchent doit être le même.
On appelle Li1 et Li2, respectivement la distance par rapport au début à laquelle A1 (moto) prend Ai et la distance par rapport à la fin à laquelle A1 dépose Ai. On a Li1+Lli2=L:
La distance parcourue par la moto est :
D= (60-L22)+(60-L22-L31)+(60-L31-L32)+(60-L32-L41)….+(60-L(n-1)2-Ln1)+(60-Ln1)= (2n-3)60 -(2n-2)L (car L22=Ln1=L)
Si on égale les temps de A1 (moto) et de A2 .
((2n-3)60-(2n-2)L-(60-L))/50=L/5
L(7+2n)=120(n-2)
L=120(n-2)/(7+2n)
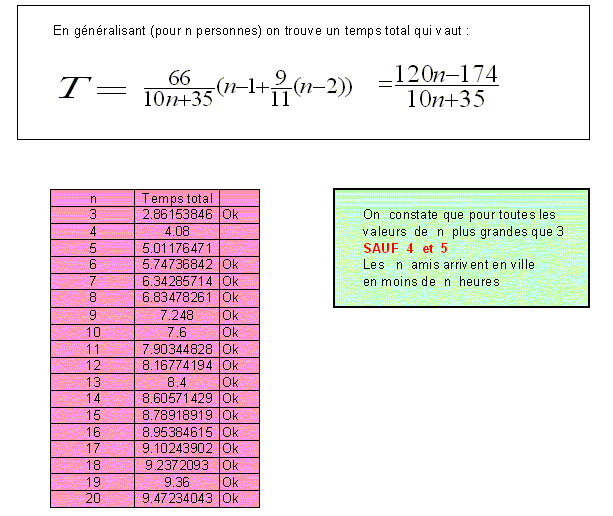
Le temps de trajet est donc égal à T=(60-L)/50+L/5=(120n-174)/(10n+35)
Il faut étudier le signe de F(n)=(120n-174)/(10n+35) -n
Soit F(n) = -10n2+85n-174
Les racines sont 3,43 et 5,06.
Entre ces racines (c'est à dire pour n=4 et n=5), la fonction est positive et donc les amis seront en retard, sinon ils pourront être à l'heure quelque soit n. Il suffira que tous partent en même temps et que A1 dépose A2 à 120(n-2)/(7+2n) de l'arrivée.

Posté par jver jver

Il me semble que ce n'est pas possible.
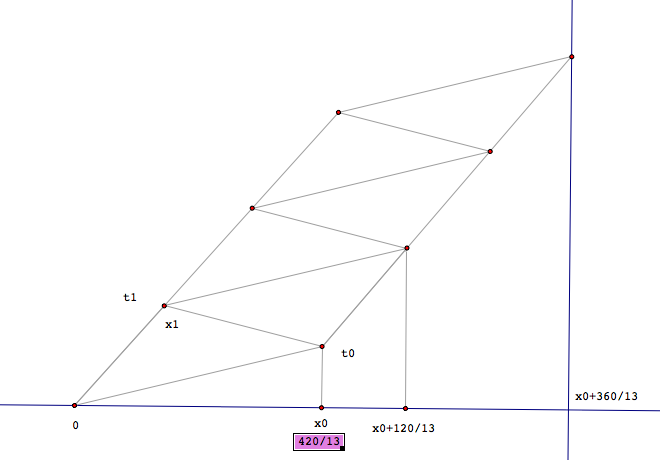
Le croquis joint montre pour 5 personnes (RV avec une sixième)
Entre deux "déposés" d'une personne se passent, sauf erreur, 120/13 heures
La première est donc à laisser en x0=420/13.
Le temps total est donc le temps pour parcourir 420/13 en vélo, augmenté du temps pour parcourir 360/13 km à 5 km/h.
L'heure d'arrivée est donc:
1/50 420/13+1/5 360/13=402/65 heures, soit de l'ordre de 6,18h, nettement supérieur à 5h.

Donc, sauf erreur ou sauf stratégie meilleure, la réponse est "non"

Posté par malice904 malice904

non ils ne peuvent pas

Posté par lo5707 lo5707

Connaissant la première, je connais aussi celle-ci:

k-1 amis parcourent la même distance X à pied et 60 - X sur le vélo tandis que le cycliste parcourt (k-1)*(60-X) dans un sens et (k-2)60 - (k-1)X dans l'autre.

D'où X = 120(k-2) / (2k+7) et la durée totale du parcours est T = 6(20k - 29) / 5(2k+7).

On vérifie que pour k=3 et k=4, on retrouve bien les valeurs déjà calculées.

Le temps de parcours T est inférieur à k heures si 6(20k-29) / 5(2k+7) < k. L'inéquation du second degré est satisfaite pour toute valeur de k extérieure à l'intervalle . Les seules valeurs de k intérieures à cet intervalle sont 4 et 5. Les k amis arriveront donc en retard sur un horaire de k heures s'ils sont 4 ou 5. Ils seront toujours à l'heure dans les autres cas.

Il est facile de voir que si les amis sont très nombreux, ils feront pour l'essentiel de la marche à pied et la durée du trajet sera au maximum de 12 heures (en supposant bine entendu qu'ils supportent la cadence de 5 km/h sur une aussi longue distance?).Pour tout k>12, ils arriveront donc bien à la ville avant k heures.


Merci pour l'énigme.

Posté par evariste evariste

Tout le monde part en même temps de A, 2 en vélo et n-2 à pied.
Le cycliste dépose son passager à une distance x de B. Le passager fini à pied et le cycliste fait demi tour pour aller chercher un piéton. Il le prend en charge et va le déposer plus loin de façon que le piéton ait parcouru au total la distance x à pied. Et ainsi de suite.
Les n-1 piétons auront parcouru x km à pied et 60-x km en vélo. Ils arriveront dont tout ensemble en B. Il auront tous mis le même temps T, y compris le cycliste.
Pour n=3      T=(180-4x)/50=x/5 + (60-x)/50
Pour n=4      T=(300-6x)/50=x/5+ (60-x)/50

Pour n          T=((2n-3)60-(2n-2)a)/50=x/5 +(60-x)/50
A= 120 (n-2)/(2n+7)
T = 1,2 (20n-29)/(2n+7)

T>n pour n=4 et n=5, dans tous les autres cas T<n
Si n augmente T tend vers 12 h, soit le temps nécessaire pour parcourir la distandce AB à pied.

Posté par manpower manpower

Bonsoir,

en avant pour la généralisation !

Examinons d'abord le cas n=4.
C'est le même principe que le cas 3 avec un aller-retour en plus en vélo pour chercher le quatrième larron.
Cela se découpe en 5 étapes et nous conduit à 5 équations (sur le même principe que le cas précédent):
  5t1+5t2+50t3+5t4+5t5=60
  5t1+5t2+5t3+5t4+50t5=60
  50t1-50t2+50t3-50t4+50t5=60
  50t1+5t2+5t3+5t4+5t5=60
Mais les retours à vélo (temps t2 et t4) peuvent être compilés en une seule étape, d'où un nouveau système (sous forme matricielle):
50 5 5 5 ! 60
5 50 5 5 ! 60
5 5 50 5 ! 60
50 50 50 -50 ! 60  
ayant pour solution t1=t2=t3= et t4=.
Le temps total est donc de t=  ( ou ).
Et là, petite déconvenue les 4 amis ne pourront pas descendre en dessous de 4,08h !
Ici encore, une seule personne effectue les aller-retour pour chercher ceux qui marchent et les trajets des autres sont parfaitement identiques (ils marchent et pédalent le même temps (mais pas au même moment) pour arriver en même temps à l'arrivée).
On pourrait résoudre les systèmes (n,n) avec (n-1) équations du type 50 5 5...  5 ! 60 et une équation du type 50... 50 -50 ! 60 pour déterminer une formule générale (j'ai fait quelques tests, il y a bien généralisation possible).
Mais, fort du constat précédent, en changeant le fusil d'épaule et en raisonnant cette fois sur la distance d parcourue à pied par les (n-1) amis qui marchent tandis que le dernier fait des aller-retour, le tout en une équation:
(n-1) amis parcourent d km à pied et donc 60-d à vélo.
Celui à vélo parcoure lui (n-1)*(60-d) avec les amis pour les avancer et (n-2)*60-(n-1)d en arrière pour les chercher

Le temps total est t=d/n+(60-d)/50=(n-1)*(60-d)+(n-2)*60-(n-1)d
On en déduit, après simplifications, que d=
puis que t= ou encore
Enfin, la condition de temps, se traduit par <n, ce qui revient à l'étude de signe du polynôme 10n²-85n+174>0.
Le discrimiant vaut 265 et les racines sont .
, et le polynôme est du signe de a(=10) à l'extérieur des racines donc les valeurs de n comprises entre n1 et n2 sont à exclure, i.e. 4 mais aussi 5 (avec un temps total de ) ne conviennent pas.

Conclusion: Dans le cas général, pour n amis:
Si n=1, impossible (il mettrait 1,2 heure)
Si n=2, impossible également (en laissant le vélo à la moitié ils mettraient 6,6 heures dont 36 min en vélo)
Si n=3, possible en (cf enigma 23)
Si n=4 ou 5: impossible (cf ci-dessus)
Si 6n11, possible (dans un temps total de heures)
Si n12, possible et trivial : ils marchent tous par exemple !! (mais la formule précédente convient encore pour aller plus vite).

Finalement, seul les cas n=1,2,4,5 sont impossibles. Ouf !

Merci pour cette énigme passionnante.

Posté par infophile infophile

Bonjour



Démonstration

Comme dans l'énigma précédente on désigne parmi les amis un responsable de la bicyclette.

Les amis restants parcourront comme tantôt une distance à pied et à bicyclette.

En faisant un dessin (blindé de zigzags ) on s'aperçoit que le responsable de la bicyclette devra parcourir km à « l'aller » et au « retour ».

Ainsi l'équation que l'on avait obtenue s'écrit maintenant :



Soit en réduisant au même dénominateur :



D'où

Reportons dans le membre de gauche pour obtenir la durée :



Soit

On veut déterminer les valeurs de pour lesquelles

En remplaçant par son expression on obtient l'inéquation suivante :



Et l'étude de ce trinôme montre que l'inégalité est vérifiée pour tout n excepté pour et où on a respectivement -6 et -1.

Merci pour l'énigme

Posté par plumemeteore plumemeteore

rebonjour
là encore il y a un pilote permanent et chacun des (n-1) autres devra marcher d km, car lors d'une rencontre-changement il est équivalent que le pilote reste sur la bicyclette ou cède sa place; d'autre part, toute inégalité cause une augmentation du temps du fait de celui qui doit marcher le plus
les points de prise en charge seront espacés de d/(n-2) km; de même les points de dépôt
entre deux prises de passagers, le pilote devra effectuer 60-d km avant de déposer son passager, puis 60 - d - d/(n-2) pour aller rechercher le suivant
calcul de d en fonction de n
60 - d + 60 - d - d/(n-2) = 10*d/(n-2)
120 - 2d - d/(n-2) = 10d/(n-2)
120n - 240  - 2nd + 4d - d = 10 d
la réponse est oui, quel que soit n
120n-240= 10d+2nd-4d+d = d(7+2n)
d = (120n-240)/(7+2n)
somme des n-2 parcours égaux du pilotes entre les prises des premiers et derniers passagers :
(n-2)* (120 - 2d - d/(n-2))
= 120n-240-2dn+4d-d
en ajoutant le parcours 60-d avec le dernier passager :
120n-180-2dn+2d
= 120n-180+d(2-2n)
= 120n - 180 + (2-2n)(120n-240)/(7+2n)
= (840n + 240n² - 1260 - 360n + 240n - 480 - 240n² + 480n) / (7+2n)
= (1200n-1740)/(7+2n)
temps en heures : (24n-34,8)/(7+2n)
(24n-34,8)/(7+2n) < n
24n-34,8 < 7n+4n²
4n²-17n+34,8 > 0
le discriminant du nombre de gauche est négatif et le coefficient en n² est positif : le membre de gauche est positif
quel que soit le nombre n de personnes, elles mettront toujours moins de n heures

Posté par Daniel62 Daniel62

Bonjour à tous.

Je pensais ne pas répondre à cette question qui me paraissait assez difficile, mais après analyse il s'avère que ce n'est pas tout à fait impossible, à condition déjà d'avoir bon à la question précédente, et vu la gueule de la bicyclette, je risque fort d'avoir non pas un mais deux poissons carrés ...!

la question est: peuvent-ils arriver à la ville en moins de n heures?
ma réponse est: NON

bon il faut aussi une démonstration
dans un premier temps je dirais qu'il suffit de trouver un seul cas pour justifier ma réponse.
ce cas me parait évident lorsque n=1 la vitesse est de 50Km/h donc impossible de faire les 60km en une heure.
mais c'est un cas particulier (surtout qu'il y a un s dans "n amis")
je supposerais donc que n > 1

pour le cas n = 2, c'est plus facile, 2 personnes sur une bicyclette roulant à 50Km/h vont mettre 1 heure 12 minutes pour faire 60Km donc moins de 2 heures

pour le cas n = 3 voir ma réponse précédente, la vitesse moyenne est de
soit de 20,96 Km\h qui est supérieure à

donc jusqu'à présent à part le cas n = 1 que j'ai exclu, la réponse devrait être oui et pourtant il y a d'autres cas où ce sera non.

je reprends ma formule précedente:
   soit un temps qui reste à déterminer (et qui s'éliminera au calcul de la vitesse)
   distance=
   temps =  
   vitesse =

il faut étapes pour n amis (on voit que le cas n=1 est exclu)
il y a trois groupes: 2 groupes de marcheurs et une bicyclette qui fait la navette entre les 2 groupes avec 2 personnes à l'aller et 1 personne au retour.
on remarque qu'entre les 2 groupes de marcheurs, la distance est toujours la même soit ce qui veut dire que les temps de parcours pour la bicyclette vont se repéter à l'aller et au retour.
   de la formule précédente je tire la formule générale en répètant les 2 derniers termes (n-2) fois
   distance=
   temps =  
   j'en tire la vitesse et je simplifie:
   vitesse =    (avec n entier et n > 1)

je dois comparer cette vitesse à si plus petite, ils n'arriveront pas à l'heure.
pour cela je fait la différence entre les 2 vitesses
après reduction au même dénominateur je trouve:
  
le numérateur s'annule pour 2 valeurs 3,436 et 5,063
entre ces deux valeurs on trouve n=4 et n=5   
ces deux cas et à mon avis ce sont les seuls (n=1 étant exclu) justifient ma réponse.
pour n=4 la vitesse est de 14,70 qui est inférieure à 15 (retard de 4 minutes 48 secondes)
pour n=5 la vitesse est de 11,97 qui est inférieure à 12 (retard de 42 secondes)
à partir de 6 c'est bon:
pour n=6 la vitesse est de 10,439 qui est supérieure à 10 (avance de 15mn 9s)
ça va même de mieux en mieux:
pou n=10 la vitesse est de 7,894 qui est supérieure à 6 (avance de 1h 36mn)

conclusions:
avoir le plus d'amis possible mais surtout pas 4 ou 5 et si t'es tout seul il vaut mieux rester chez toi.

Posté par piepalm piepalm

Généralisation de la solution:
Si t est le temps passé à rebrousser chemin, et t+6/5 le temps passé à aller de l'avant, puisqu'il y a n-1 marcheur pendant le temps t et n-2 pendant le temps t+6/5, le produit de la distance parcourue par le nombre de personnes est 60(n-1)=50t+60+(n-1)5t+(n-2)(5t+6)=(10n+35)t+(6n+48), soit t=(54n-108)/(5(2n+7)), et T=2t+6/5=(120n-174)/(5(2n+7).
On aura T<n si 5n(2n+7)-120n+174>0 soit 10n^2-85n+174>0: les racines du trinôme sont (85+-rac(265))/20 soit environ 3,44 et 5,06.
Il en résulte que  le trinôme en n est négatif pour n=4 et 5 et positif pour les autres valeurs de n: il est donc possible d'arriver en moins de n heures pour toutes les valeurs de n sauf 4 et 5.
On vérifie que pour n=4 et 5, T vaut respectivement 4,08 et 5,01

Posté par rogerd rogerd

Bonjour Monrow et merci.

Soient P0,P1,...Pn-1 les noms des n amis, P0 étant celui qui reste sur la bicyclette. Essayons de voir les choses plus globalement que dans l'énigme 23.

Pour que le trajet soit le plus rapide possible, il est clair qu'il faut que tout le monde avance à chaque instant, soit à pied soit à 2 dans le bon sens sur  le vélo soit dans le mauvais sens seul sur le vélo.

Si P1 arrive avant P2, c'est qu'il a passé plus de temps sur le porte-bagages. Il doit attendre P2 et ce temps supplémentaire sur le vélo aura été gaspillé. Dans la solution optimale, P1,..Pn-1 passe donc le même temps sur le porte bagage et les n trajets ont la même durée (y compris pour P0, qui arrive en même temps que Pn-1 qui est sur son porte-bagages).

P0 a fait des allées et retour. S'il a fait x km dans le bon sens, il a fait x-60 km dans le mauvais sens donc 2x-60 km en tout, à la vitesse 50. La durée commune aux n trajets de nos n amis est donc de (2x-60)/50.

Si chacun de P1,..Pn-1 a fait k km à pied et 60-k km sur le porte bagage cette durée commune des n trajets s'écrit aussi k/5+(60-k)/50 soit (9k+60)/50

Enfin, les x km faits par P0 dans le bon sens sont ceux faits avec quelqu'un sur le porte-bagages donc x=(n-1)(60-k).

Ces relations entre x, n et k me permettent d'exprimer la durée du trajet en fonction de n uniquement. Je trouve (120n-174)/(10n+35).

En écrivant que cette durée doit être inférieure à n, je tombe sur une inéquation du 2°degré: 10n^2-85n +174>=0.

Elle n'est pas satisfaite pour n=4 et n=5. Je peux déjà dire

S'ils sont au nombre de 4 ou 5, nos amis ne pourront être à l'heure au rendez-vous.

Pour les autres valeurs de n entier >2, l'inéquation est satisfaite mais
cela ne veut pas dire pour autant que ça marche.

Encore faut-il trouver une façon de gérer les allées et retour du vélo de façon à ce que le trajet dure moins de n heures.

Pour n=3, on sait déjà (énigme précédente) que c'est possible. Continuons avec n>=6.

J'essaie avec la gestion qui paraît la plus naturelle:
P0 part avec P1 sur le porte bagage, le dépose au bout d'un temps t1 et revient chercher P2 qui avait commencé à pied et qui reste à son tour un temps t1 sur le porte-bagage. On recommence jusqu'à ce que P0, avec Pn-1 sur le porte-bagage, rattrape le peloton des marcheurs P1,...Pn-2.
Je détermine alors t1 de façon à ce que cette ultime rencontre se fasse au 60°km.
Je calcule alors la durée du trajet( en ajoutant des petits morceaux) et je trouve (120n-174)/(10n+35), dont je sais que c'est plus petit que n (puisque l'inéquation est satisfaite. Donc:

Pour n supérieur ou égal à 6, il y a une stratégie permettant d'arriver à l'heure

Ouf!

Posté par PloufPlouf06 PloufPlouf06

Bonjour,

Je vais reprendre mon raisonnement de l'énigme 23, c'est-à-dire que la bicylette dépose deux premiers amis jusqu'à un certain point, puis revient en chercher deux autres qu'elle ramène jusqu'au deux premiers et ainsi de suite.
En image, le premier cycle du trajet de la bicylette :


On fixe la durée d'un aller égale à t.
Calculons alors la durée du retour de la bicyclette jusqu'au premier groupe de piétons :
Après le premier dépôt, le premier groupe de piétons a donc pour abcisse : et le deuxième groupe de piétons
La bicyclette rencontre le groupe A après une durée t' telle que : soit .
La durée d'un retour est donc de .
Etant donné que les groupes de piétons avancent à la même vitesse, la distance qui les sépare est constante. Par conséquent, la durée d'un aller et celle d'un retour sont également constantes aux valeurs données précédemment.

Pour n amis à transporter, cherchons la durée des d'aller-retours nécessaires. On ne traite que le cas où n est pair (dans le cas où n est impair, les résultats seront les mêmes que ceux du pair suivant, soit n+1).
Pour transporter les n amis, il faut aller-retours, avec un aller supplémentaire. Si on appelle T la durée totale de l'opération, on a donc :
Au bout d'une durée T, l'opération étant terminée, on a : . De plus, car durant les premiers aller-retours, le  groupe des piétons se déplace à pieds, tandis que le dernier aller se fait à bicylette.
On a donc à résoudre : . On trouve ainsi : que l'on remplace dans l'équation donnant la durée totale T.

Finalement, la durée optimale du déplacement de n amis est : .
Cette formule est vérifiée pour n=2 (résultat identique à n=1) où le résultat est , résultat également obtenu par une règle de trois.
Elle est également vraie dans le cas où n=4 (résultat identique à n=3)c'est-à-dire la situation de l'énigme 23, qui donne une durée minimale (au moins si j'ai faux aux deux énigmes, je suis cohérent dans ma bétise )

Il reste à vérifier que
Soit la fonction f(n) définie par . Après factorisation,
Le dénominateur est strictement positif pour n entier naturel non nul.
Etudions le signe du numérateur : Il n'y a donc pas de solution réelle, donc pas de solution naturelle.
Le numérateur est donc strictement négatif. On a donc :

Les n amis arriveront donc toujours en moins de n heures.

On peut même remarquer que quelque soit le nombre d'amis, ils arriveront en moins de 12h, car ce qui est assez surprenant à mon goût .

Merci pour cette énigme, en espérant un .

Posté par gloubi gloubi

Bonjour,

Si on regarde mon schéma de l'énigme précédente

on voit que la distance de 60 km qui valait 130d/11 "augmente" de 20d/11
chaque fois qu'on augmente n de 1. (en fait, c'est d qui diminue, bien sûr)

De même, chaque fois que n augmente de 1, la distance parcourue par le vélo
augmente de 200d/11.

Au final, le temps total T pour relier les deux villes est

heures = heures

Pour n = 1 et n = 2, le temps entre les deux villes est 60/50 = 1,2 h.
Pour n 3 la formule précedente donne:
n = 3 , T 2,86 h
n = 4 , T 4,08 h
n = 5 , T 5,01 h
n = 6 , T 5,75 h
n = 7 , T 6,34 h
n = 8 , T 6,83 h
n = 9 , T 7,25 h
n = 10 , T = 7,6 h
ensuite T est toujours < 10 (limite = 20/2 = 10 heures quand n )

Les seules valeurs de n pour lesquelles le temps mis pour relier les deux villes
est supérieur à n heures sont n = 1, n = 4 et n = 5.

Sauf distraction.

A+,
gloubi

Posté par gloubi gloubi

Re-

N'importe quoi! La limite de T quand n tend vers l'infini est 12 heures, pas 10.
J'aurais du ajouter:
n = 11, T 7,9 heures
n = 12, T 8,17 heures

Merci pour le

gloubi

Posté par dhalte dhalte

Bonjour.
Généralisation :

S'ils sont 3, ils mettent 2h51'41", donc moins de 3 heures
S'ils sont 4, ils mettent 4h4'48", donc plus de 4 heures
S'ils sont 5, ils mettent 5h0'42", donc plus de 5 heures
S'ils sont 6, ils mettent 5h44'50", donc moins de 6 heures
S'ils sont 7, ils mettent 6h20'34", donc moins de 7 heures
Et la différence entre la durée et le nombre d'amis ne cesse ensuite de décroître.

L'étude théorique montre que le signe de la différence entre le temps de transport et le nombre d'amis implique une loi binomiale qui justifie qu'il n'y ait pas d'autres cas à envisager.

Temps optimal : sera obtenu si les personnes sont constamment en mouvement durant tout le processus.

L'idéal est donc que les trois arrivent tous en même temps.

On envisage le processus récurrent suivant :
A un moment donné, un groupe A de p personnes est à un endroit donné, en compagnie du vélo et un groupe B de n-p personnes est situé entre ce groupe et l'arrivée.
Puis un cycliste et un passager se dirigent vers le groupe B, tandis que les deux groupes continuent leur progression.
Puis le cycliste dépose son passager auprès du groupe B et repart vers le groupe A. Les deux groupes continuent leur progression.

Etape initiale : Le groupe A, de n-2 personnes, démarre en même temps que le cycliste et son passager. Celui-ci laisse son passager à une certaine distance pour revenir vers le groupe A tandis que le passager continue son chemin.
Quand le cycliste rejoint le groupe A, la distance qui sépare les deux groupes est appelée 'd'.

Etape finale : le groupe A est réduit à 1 personne plus le cycliste. Ils partent en vélo vers le groupe B et le rejoignent au moment où celui-ci atteint l'arrivée.

Vitesse du marcheur : v0, du vélo : v1, distance totale à parcourir : D

On remarque tout de suite que, les groupes de marcheurs se déplaçant à la même vitesse, leur écart est constant. Il vaut justement cette valeur 'd'. Donc l'étape initiale est assimilée à la première des étapes récurrentes, où le groupe B était tout simplement vide.

Nombre d'allers-retours qu'effectue le cycliste pour transporter ses passagers pendant la phase récurrente (c'est à dire sans le transport du dernier passager) : n-2.

Soit t1 la durée du transport de A vers B : lorsque le vélo démarre, le groupe B est à la distance d. Puis quand il rejoint le groupe B, celui-ci a encore avancé d'une distance = v0 t1.
v1 t1=d+v0 t1 : (v1-v0)t1=d
Soit t2 la durée du transport de B vers A. lorsque le vélo démarre, le groupe A est à la distance d. Puis quand il rejoint le groupe A, celui-ci s'est rapproché d'une distance = v0 t2.
v1t2=d-v0t2 : (v1+v0)t2=d
Donc la durée totale des n-3 allers retours est de (n-2)(t1+t2)=(n-2)d(1/(v1-v0)+1/(v1+v0))

Pendant cette durée, les groupes A et B parcourent la distance (n-2)(t1+t2)v0.

La distance finale f que franchit le groupe B est telle que le vélo, qui est auprès du groupe A à une distance d en arrière, le rejoigne sur la ligne d'arrivée en un temps égal. Le vélo doit donc franchir une distance d+f. Soit t3 ce temps. Alors on a
t3v1=d+f
t3v0=f
Ce qui donne
t3(v1-v0)=d
Le temps de trajet total T est T=(n-2)(t1+t2)+t3
La distance totale franchie vaut D et on a D=(n-2)(t1+t2)v0+d+f

On obtient donc la formule permettant de calculer d :
D=d(1+(n-1)v0/(v1-v0)+(n-2)v0/(v1+v0))
Et ensuite, T
T=d((n-1)/(v1-v0)+(n-2)/(v1+v0))

D'où l'expression complète de T



Etude du signe de T-n, dans le cadre de l'application numérique…
D=60, v0=5, v1=50

Comme n est positif, cette quantité est du signe du numérateur et donc positive entre les racines.
Les racines sont
, de valeurs approximatives
3,43605897
5,06394103
Ce qui confirme les résultats présentés au début.

Posté par torio torio

Voir première énigme "à bicyclette"
pour la pose des équations.
A+
Torio

Posté par veleda veleda

bonjcour Monrow

*si n=2 la bicyclette permet aux deux amis  de faire le trajet en (6/5) h donc d'arriver  au rendez vous avec(3-6/5)60minutes d'avance c'est à dire 108 minutes
*si n>2
remarquesi n12 un piéton peut parcourir les 60km en n heures donc une solution est de laisser le vélo et de partir ensemble à pieds  mais ce n'est certainement pas la solution optimale

je propose le même principe que pour n=3
si {X_i}pour 1in est l'ensemble des amis
à t=o X₁et X₂ partent en vélo tandis que les autres partent à pieds
en A(t)situé entre O et le lieu de rendez vous :
X₁ continue en marchant
et
X₂ fait 1/2 tour pour aller à la rencontre du peloton de piétons qu'il rejoint en B(t')l'un des piétons ,X₃ par exemple repart à vélo vers le lieu de rendez vous avec X₂,ils rejoignentX₁ en R₁(t")
avec les notations de l'énigme précédente  t"=t+t' et t'=(20/11)t
il y a n-2 piétons à rapprocher du marcheur de tête ,la durée d'un aller et retour du vélo    pour rapprocher un marcheur est t' et il y a n-2 marcheurs à rapprocher

au temps T=t+(n-2)t'=t+(n-2)(20/11)t=(20n-29t/11 les n amis sont regroupés en R_n-2avec OR_n-2=50t+5(n-2)(20/11)t=50(1+2(n-2)/11)t=50(7+2n)t/11
ils seront au point de rendez vous si OR_n-2=6O =>t=66/(35+10n)
d'où
T=(6/5)(2On-29)/(7+2n)
il reste à écrire Tn
cela se traduit parf(n)=10n²-85n+1740
les zéros de f sont x'=3,43 et x"=5,06 (valeurs par défaut )
f(n)0 <=>( n<4 ou n>5 )        
en conclusionsi les amis sont 4 ou 5  ils ne seront pas à l'heure aurendezvous les retards étant trés faibles du reste
merci pour cette enigma

Posté par 1emeu 1emeu

Bonjour,

je trouve le résultat amusant suivant,

les n amis arriveront au village situé à 60 km en moins de n heures si et seulement

Preuve :

On supposera qu'un des amis est attaché au vélo (sans perte de généralité). On a donc n-1 amis qui doivent se partager la place sur le porte bagage

En n heures, le vélo peut parcourir 50*n km. Il en parcourera vers l'avant et vers l'arrière. Dans le meilleur des cas, les n-1 amis non liés au vélo se partageront équitablement le nombre de kilomètres sur le porte bagage (dans le cas contraire, celui qui aura le moins accès au vélo arrivera en dernier et le temps total sera moins bon).

Par conséquent, dans le meilleur des cas, pour chacun des n-1 amis, le nombre de kilomètres effectué sur le porte bagage sera inférieur à

Notons le nombre de kilometres effectué par chacun des n-1 amis sur le porte bagage. Alors, le temps mis pour arriver est


Or si et seulement si .

On en déduit le résultat (en considérant ) :
les n amis peuvent arriver au village situé à 60 km en strictement moins de n heures si et seulement

En effet, voici comment on procède pour trouver l'itinéraire :
soit , on choisit tel que et . Un des amis prend la bicyclette et un passager sur le porte bagage et l'avance de kilomètres. Puis il le dépose et repart en arrière pour chercher un autre ami et l'avance de même de kilomètres. Il procède ainsi jusqu'à avoir avances chacun de ses amis de kilomètres, puis va au village d'arrivée. D'après la construction ci-dessus, tous les n amis arriveront alors avant la dead line fatidique des n heures

Merci pour l'énigme (très intéressante !!) ,

1emeu

Posté par totti1000 totti1000

Partons du meme principe que celui avec trois personnes... C'est à dire trouver les points où déposer les différents amis,
pour qu'à la fin tous arrivent en meme temps. Voir dessin.
Tout d'abbord il est bon de noter que pour n>12 les amis mettrons forcement moins de n heures, en effet en faisant, tout le parcour à pied
ils mettent 12h...

Pour n=1, il met 1h12min, soit plus de 1 heure.
Pour n=2, ils mettent 1h12min, soit moins de 2 heures.
Pour n=3 on l'a deja vu ils mettent 2h52min (les temps sont arrondis à la minute...), soit moins de 3 heures.

En faisant de meme, on a pour n=4 un systeme de 6 équations à 6 inconnues, qui sont (voir dessin) les suivantes:
a/5=x/50
(r1-a)/5=(x-r1)/50
(b-r1)/5=(y-r1)/50
(r2-b)/5=(y-r2)/50
(x-r1+y-r1)/50=(y-x)/5
(y-r2+60-r2)/50=(60-y)/5

On trouve alors x = 44, et donc un temps de parcour de 4h05min, soit ici plus de 4 heures...

Pour n=5 on a un système de neuf équations à neuf inconnues, on  trouve un temps de 5h01min, c'est plus de 5 heures...

Pour n=6 on trouve 5h45min soit moins de 6 heures...

On remarque alors que le premier point où est déposé le premier amis, est:
660/11 pour n=2,
660/13 pour n=3,
660/15 pour n=4,
660/17 pour n=5 etc...

En général c'est en fait x=660/(7+2n), soit un temps de parcours en général de x/50 + (60-x)/5 d'où après simplifications
un temps de parcours égal à 12-(594/(35+10n)) ceci pour n>1 (le cas n=1 a été traité au début)...
On cherche donc les n tels que 12-(594/(35+10n))>n, on arrive a -10n²+85n-174>0, ce polynome de degré 2 a deux solutions
x1 et x2, on a alors x1<n<x2 avec x1≈3,44 et x2≈5,06 d'où n=4 ou n=5...

POUR RESUME:

Nos amis mettront moins de n heures pour tout entiers n different de 1, 4 et 5.
En effet les seuls cas  où ils mettront plus de n heures sont 1 (1h12min), 4 (4h05min) et 5 (5h01min)...

On peut voir sur le shéma le petit graphique qui donne la répartition selon n, cette suite tend vers 12, ce qui était prévisible, en effet plus il y a d'amis et plus
le premier est déposé près du km 0 et donc tend à faire les 60km à pieds (soit tend vers 12h de trajet)...

Posté par kiko21 kiko21

Bonjour,

Je trouve la fonction suivante qui exprime le temps de parcours optimal exprimé en heure t en fonction du nombre d'amis n :

Il faut étudier le signe de

On résout 10n²-85n+174=0 et on trouve deux solutions :



n - t(n) est négatif (du signe de -a = -10 car 10n+35 toujours positif pour n positif) entre n13,44 et n25,06

Effectivement, on a t(4) 4,08 h > 4 et t(5) 5,16 h > 5
Pour ces 2 cas, on t>n

Pour toutes les autres valeurs de n>5 on aura toujours t(n) < n
Si on calcule la limite de t(n) pour n tendant vers +, on trouve 12^-

Cas particuliers où la formule de t(n) n'est pas applicable :
n=1 ; t=1,2 h  t>n
n=2 ; t=1,2 h  t<n

En conclusion, n amis ne peuvent pas arriver à la ville en moins de n heures car  il y a trois cas n=1 n=4 et n=5 ou t>n

Merci et A+, KiKo21.

Posté par 1emeu 1emeu

oups, un peu tard, mais j'avais oublié la cas n=1 qui est bien sûr impossible.

La solution que je propose est alors :
les n amis arriveront à l'heure au rdv si et seulement si

Posté par bizbiz bizbiz

Salut,
Je pense que j'ai trouvé ...

Voici l'expression du temps [h] en fonction du nombres de personnes ( car comme même ! )   :

Ensuite, en posant : et en supposant que x est réel, on a après calcul :

Resolution de :


            

Pour   :
C'est-à-dire que dans ce cas :

Ailleurs :

Donc, en reprenant le cas quand x est entier (car le nombre de personnes et toujours entier ), on a :

quand : avec :  

Pour on a :.

Cas particulier:   :  on a : h , donc : .

Ma réponse sera donc :



Merci et A+

Posté par Poldenys Poldenys

Enigma 24
J'appelle t1 l'instant choisi par le cycliste pour déposer son 1er passager et faire demi-tour .
Il a alors parcouru la distance x0 , t2 l'instant où il prend en charge son 2è passager , et
ainsi de suite t3 (2è point de retour), t4 ,..., jusqu'à t2n-3 = tA instant de l'arrivée commune
des n amis . Equations horaires des 2n-3 tronçons du cycliste : 1er aller:  
1er retour:     2ème aller:     2ème retour :      3ème aller:      3ème retour:
..........................................................................................
kième aller:    kième retour;
........................................................................................
(n-1)ème et dernier aller : soit
Equation horaire du 1er "passager-piéton" : et celle du dernier "passager-piéton": .Ces 2 dernières équations forment avec celles du premier et du
dernier tronçons du cycliste un parallélogramme sur la représentation graphique .
Calcul de :les coordonnées du point A (arrivée commune) vérifient les équations du
dernier "tronçon cycliste": et celle du dernier "passager-piéton":de ces 2 égalités je tire: et d'où et

d'où     puis je calcule à partir de

.Je calcule maintenant le signe de
le dénominateur est positif j'étudie le signe du trinôme au numérateur  .Le trinôme et
sont positifs quand n est à l'extérieur de l'intervalle des racines .Résolvons l'équation
solutions: et
.Seules 2 valeurs entières sont dans cet
intervalle n=4 et n=5 .Pour ces 2 valeurs les n amis ne serons pas à l'heure au rendez-vous .
Il faut également éliminer n=1 et n=0 bien entendu !Pour toutes les autres valeurs ça marche !
.Pour les premières valeurs de n : pour n=3 nous avons plus 8 min d'avance , pour n=4 un retard de 4 min 48s , pour n=5 un retard de plus de 42s , pour n=6 une avance de plus de15 min , pour n=7 une avance  plus de 19 min et pour n=8 une avance de plus de 1 heure .

Posté par monrow monrow

ENIGME CLOTUREE

Merci pour votre participation

Posté par torio torio

Le poisson vient-il du fait que je n'ai pas mentionné les cas triviaux n= 1 et n=2 ?

Encore merci pour cette énigme !!!

Posté par kioups kioups

triviaux, triviaux... ce sont les seuls cas que j'avais...

En tous cas, bravo pour ceux qui ont réussi (ou approchées), j'adore lire vos résolutions !

Posté par lyonnais lyonnais

torio >

Je pense que tu n'as pas respecté dans ta réponse cette consigne :

Posté par rogerd rogerd

Bonsoir Monrow

Il me semble que tu demandais une démonstration...

Je te suggère de relire soigneusement celles qui t'on été proposées..

Posté par rogerd rogerd

celles qui t'ont été proposées..

Posté par plumemeteore plumemeteore

Une solution assez courte.
Les piétons sont pris à intervalles constants et déposés de même.
Le nombre i d'intervalles est n-2; soit k la longueur d'un intervalle en kilomètres.
Chaque piéton doit marcher ik et est véhiculé 60-ik
Son trajet dure 0.2 ik + 1.2 - 0,02ik = 1,2 + 0,18ik
Calcul de k en fonction de i
Entre deux prises en charge, le cycliste fait 120 - 2ik - k kilomètres
Pendant ce temps, le piéton marche k kilomètres.
120 - 2ik - k = 10k; 11k + 2ik = 120; k = 120/(11 + 2i)
Le trajet dure 1,2 + 0,18ik = 1,2 + 21,6i/(11 + 2i) = (13,2 + 24i)/(11 + 2i)
pour arriver à temps, il faut que : (13,2 + 24i)/(11 + 2i) < i + 2
13,2 + 24i <  2i² + 15i + 22
2i² - 9i + 8,8 > 0
Le premier membre est zéro quand i = 3,06 ou i = 1,43
Il est négatif quand i = 2 ou i = 3 et positif pour toute autre valeur entière de i.
n personnes arriveront en retard si n = 2+2 = 4 ou n = 3+2 = 5 et à temps dans les autres cas.

Posté par monrow monrow

torio>> en effet,comme te l'as dit lyonnais,il fallait préciser une démo

rogerd>> tu peux bien signaler les démos que t'as pas bien accepté pour les relire. La correction n'est pas vraiment si facile que ça donc ça m'arrive des fois d'accepter un truc sans bien me concentrer. Donc signale moi les démos qui ne te semblent pas logiques et j'essaierai de revoir

Posté par rogerd rogerd

Monrow, permets moi d'abord de te rendre hommage : tu lis avec bienveillance toutes les critiques et, quand elles sont fondées, tu es toujours prêt à rectifier le tir.

Quant à l'énigme en question, je conçois qu'elle a été difficile à corriger: la seule chose évidente en première lecture est: la réponse est-elle bonne ou pas (ici: distinguer les cas n=5 et n=6). Après cela, sachant que la réponse était bonne, il était sans doute difficile de peser la qualité de la démonstration.

Ce serait bien si tu pouvais consacrer un peu de temps à les relire.
Sans parler de quelques réponses sans justification ou avec une justification fausse, je trouve que beaucoup ont considéré comme évidente la stratégie à adopter: le cycliste prend le passager P1 pendant un temps T, le dépose, reviens chercher P2, le transporte pendant le même temps T etc.. et tous arrivent en même temps à destination. Peu de gens ont prouvé que cette stratégie est optimale, parmi les mille stratégies possibles.

Posté par monrow monrow

Merci Rogerd N'hésitez jamais à poster vos remarques et critiques à propos de la correction, je puex bien faire des erreurs d'inattention

Je suis d'accord avec toi, peu sont ceux qui ont démontrer le parcours mais dans la question j'ai pas demandé le parcours comme dans l'énigme 23 j'ai juste demandé les entiers n où ils arriveraient avant n heures donc je peux pas pénaliser les autres puisque c'était pas présent dans la question

Pour relire toutes les démos dès le début ca va me prendre vraiment bcp de temps , je vais essayer mais signale ici les réponses qui te semblent fausses pour me faciliter la tâche !

Merci Rogerd

Posté par PloufPlouf06 PloufPlouf06

Bonjour à tous,

Est ce que quelqu'un aurait le courage de m'expliquer pourquoi la formule que je trouve est fausse, alors que pourtant elle vérifie trop de particularité (cf mon post) pour que ce soit une coïncidence

Merci d'avance

Posté par rogerd rogerd

PloufPlouf06
Bonjour!
Quand tu dis :

" la bicyclette dépose deux premiers amis jusqu'à un certain point, puis revient en chercher deux autres qu'elle ramène jusqu'au deux premiers "

dis-moi: qui conduit la bicyclette pendant cette phase de retour? (puisque le pilote et le passager ont été déposés!)

Posté par PloufPlouf06 PloufPlouf06

Bonjour à tous,

En effet, j'ai oublié ce léger détail Mais dans l'absolu il n'est pas précisé que la bicyclette doit être conduit par quelqu'un (non je plaisante )

Merci d'avoir regardé rogerd. Bonne journée

Posté par Flo08 Flo08

Bonjour,


... Excellente question, en effet
_{On peut supposer que le chef-ingénieur J-P a installé une nouvelle amélioration sur ladite bicyclette :  
un module de pilotage automatique
OK, je sors  -----> []}

Posté par rogerd rogerd

PloufPlouf06 et Flo08

Bonne journée à vous aussi

Posté par plumemeteore plumemeteore

bonsoir

la bicyclette pourrait être remplacée par un cheval
pour corser le problème, on pourrait assigner au cheval des vitesses différentes selon qu'il transporte zéro, un ou deux cavaliers

Posté par PloufPlouf06 PloufPlouf06

Bonsoir plumemeteore,

J'ai déjà fait le cheval qui court à une vitesse constante , après si la vitesse est différente je suis pas sûr que la difficulté soit très différente, à moins peut être qu'il se fatigue de plus en plus au cours du temps

Posté par manpower manpower

Bonsoir,

euh... pourrais-je savoir ce qui m'a valu d'être empoissonné ainsi?
ma démonstration et ma réponse me semblent justent... qu'est ce qui cloche ?

Posté par kioups kioups

Manpower : peut-être le cas n=2...

Posté par monrow monrow

Salut manpower

je suis vraiment désolé je voulais vraiment pas te donner ce poisson vu ton excellent raisonnement et tes résultats...mais ce cas n=2 était bien à éliminer

Encore une fois désolé

Posté par manpower manpower

Bonjour,

Ah ben oui quelle grosse nouille !
Et dire que j'allais oublier ces cas ! _{Pour être plus exhaustif je les ai ajouter à la fin.}
Cas n=1, tout va bien et puis cas n=2 subitement (après tous ces calculs) j'ai oublié l'origine du problème
et j'ai considéré qu'ils ne pouvaient être deux sur le vélo !!!

Voilà ce qui s'appelle prendre une gamelle !


^{Merci et pardon pour le dérangement...}

Posté par monrow monrow



Aucun prob manpower