Fiche de mathématiques
Ile mathématiques > maths 3ème > Triangle rectangle et trigonométrie
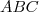tel que :
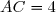cm,
)
soit la hauteur issue de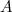 
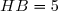cm
.
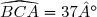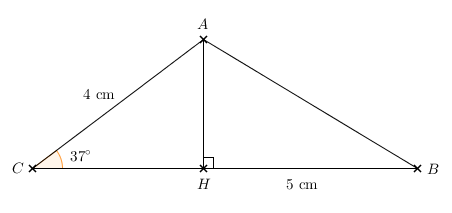
La figure n'est pas à l'échelle
Calculer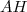
puis déterminer 
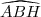(les arrondis seront donnés au centième près).
2. Montrer pour tout réel
tel que 
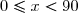on a
^2=\dfrac{1}{\left(\cos x\right)^2})
.
Publié par Prof digiSchool
le
Exercice de calcul de longueurs dans un triangle rectangle
Révisez le cours sur le triangle rectangle
exercice
1. On considère un triangleLa figure n'est pas à l'échelle
Calculer
2. Montrer pour tout réel
1. Dans le triangle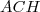 
rectangle en 
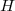on a :
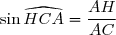
Donc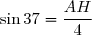
.
Par conséquent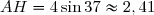
cm.
Dans le triangle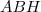
rectangle en 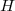on a :
.
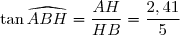Donc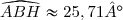
.
2. Le réel est tel que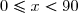 
on a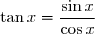 
.
Donc :
^2&=1+\left(\dfrac{\sin x}{\cos x}\right)^2 \\\\ &=1+\dfrac{\left(\sin x\right)^2}{\left(\cos x\right)^2} \\\\ &=\dfrac{\left(\sin x\right)^2+\left(\sin x\right)^2}{\left(\cos x\right)^2} \\\\ &=\dfrac{\left(\sin x\right)^2+\left(\cos x\right)^2}{\left(\cos x\right)^2} \\\\ &=\dfrac{1}{\left(\cos x\right)^2} \end{array})
Donc
Par conséquent
Dans le triangle
Donc
2. Le réel
Donc :
ceci n'est qu'un extrait
Pour visualiser la totalité des cours vous devez vous inscrire / connecter (GRATUIT)
Inscription Gratuite se connecter
Pour visualiser la totalité des cours vous devez vous inscrire / connecter (GRATUIT)
Inscription Gratuite se connecter
Voir la correction