Niveau énigmes

21 carrés pour 14 au carré

Posté par
Imod 17-06-24 à 11:58

Bonjour à tous

Certaines formules évoquent des choses : $1\times 6^2 + 2\times 5^2 + 3\times 4^2 + 4\times 3^2 + 5\times 2^2 + 6\times 1^2= 14^2 .$

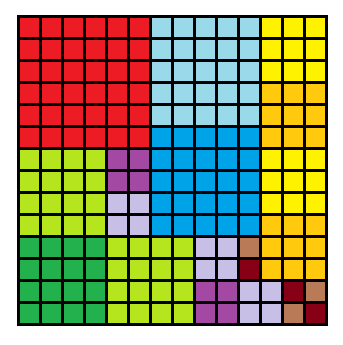
Peut-on recouvrir un carré de côté 14 avec un carré de côté 6 , deux carrés de côtés 5 , ... et six carrés de côté 1 ?

Amusez-vous bien

Imod

Posté par re : 21 carrés pour 14 au carré 17-06-24 à 15:33

Bonjour,
"échangerais volontiers 1 carré de 2² contre 4 carrés de 1"

21 carrés pour 14 au carré

Posté par re : 21 carrés pour 14 au carré 17-06-24 à 16:24

Bonjour,
comme il y a de nombreuses solutions par échanges et déplacements de blocs, il n'est pas trop difficile d'en trouver une.

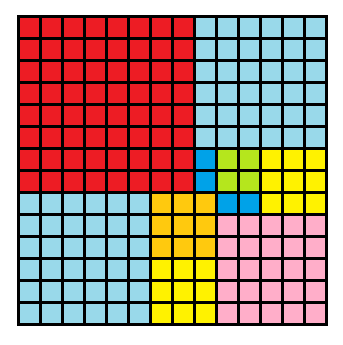
Cliquez pour afficher

on peut se poser la question de paver le 14x14 avec un minimum de carrés premiers entre eux dans leur ensemble (4 carrés de 7x7 est interdit)
l'OEIS donne pour le carré de nxn le nombre minimum de morceaux, pour le 14x14 c'est 12
alors que : 1 + 2 + 3 + 4+ 5+ 6 = 21 !

Cliquez pour afficher

Posté par re : 21 carrés pour 14 au carré 17-06-24 à 18:47

Il y a en effet beaucoup de solutions au problème mais il n'est pas si facile d'en trouver une

Pour le recouvrement par des carrés premiers entre eux , le plus difficile est de trouver la bonne décomposition en 12 carrés : il ne doit pas y en avoir tant que ça mais je ne m'y lancerais pas à la main

Imod

Posté par re : 21 carrés pour 14 au carré 17-06-24 à 19:58

premiers entre eux dans leur ensemble
c'est déjà le cas dans la découpe proposée car PGCD(6,5,4,3,2,1) = 1
et j'en ai donné une avec 12 carrés sans chercher beaucoup
ma technique est une récurrence sur la taille. mais ne garantit pas que cela donne le minimum, même s'il y a de bonnes chances que ce soit le cas.

'la doc" wolfram en donne une autre
et il y en a certainement un bon paquet.
OEIS A232484 dit qu'il y en a 323 !

par contre si on veut qu'ils soient premiers entre eux deux à deux, cela impose déja qu'ils soient tous différents, et ça ce n'est pas possible dans un carré de 14x14 (on élimine bien entendu les cas du genre un carré de 13x13 et 14²-13² = 27 carrés de 1x1 !)

le plus petit est de 110x110 en 22 carrés
mais ne donne pas premiers deux à deux vu qu'il y a deja des carrés de 2,4,6,8 ... (entre autres)
avec tous premiers deux à deux, ça doit être un carré gigantesque ! si il y en a...

de tels carrés "parfaits" (découpés en carrés tous différents) sont listés dans la doc alexandria repository