Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. TerminaleForum de terminale Autres ressourcesTopics traitant de Autres ressources [tout]Lister tous les topics de mathématiques
Niveau terminale
Partager :

a , b et c

Posté par
matheux14 11-11-20 à 15:46

Bonjour ,

Merci d'avance.

Déterminer les réels a , b et c pour la courbe représentative de la fonction f de \R vers \R définie par : f(x)=a.x+b+\dfrac{c}{x-1}  , passe par A(2 ; 4) , admette en ce point une tangente horizontale et aie au point d'abscisse 3 une tangente parallèle à la droite d'équation y=x+4.

Réponses

On a f(x)=a.x+b+\dfrac{c}{x-1}  ; D_{f}=\R \setminus \{ 1 \}

* (C) passe par A(2 ; 4).

f(2)=4 \iff 2a+b+c= 4

* (C) admet au point A(2 ; 4) une tangente horizontale.

f'(2) = 0 \iff 2a - b -c= -2

* (C) admet au point d'abscisse 3 , une tangente d'équation y={\red{1}}x+4

f'(3)=1 \iff 6a-2b-c= -2

D'où le système \begin{cases} 2a+b+c=4 \\ 2a-b-c=-2 \\ 6a-2b-c=-2 \end{cases}

Il vient a=1/2 ; b= 2 et c= 1.

Donc f(x)=\dfrac{1}{2}x+2+\dfrac{1}{x-1}.

(C) passe par A mais n'admet pas les tangentes en A..

Posté par
heklare : a , b et c 11-11-20 à 15:51

Bonjour

Revoir la dérivée de f

Posté par
chadokre : a , b et c 11-11-20 à 16:35

Effectivement  ! Dans tes 2e et 3e égalités, tu n'est pas choqué que le terme b soit encore là ?

Posté par
chadokre : a , b et c 11-11-20 à 16:36

" tu n' es" , pardon...

Posté par
matheux14re : a , b et c 11-11-20 à 18:34

Cette fois ci , je trouve  a=4/3 ; b= 0 et c= 4/3.

Donc f(x)=\dfrac{4}{3}x+\dfrac{\frac{4}{3}}{x-1}.

(C) ne passe pas par A..

Posté par
heklare : a , b et c 11-11-20 à 18:59

passe par A f(2)=4  soit 2a+b+c=4

f'(x)=a-\dfrac{c}{(x-1)^2}

tangente parallèle  à l'axe des abscisses   f'(2)=0 soit a-c=0

parallèle à la droite d'équation y=x+4 en 3  f'(3)=1 soit a-\dfrac{c}{4}=1

d'où le système \begin{cases} 2a+b+c=4\\a-c=0\\a-\dfrac{c}{4}=1\end{cases}

\begin{cases}a=\frac{4}{3}\\b=8\\c=\frac{4}{3}\end{cases}

Posté par
heklare : a , b et c 11-11-20 à 19:03

au temps pour moi b=0

\dfrac{8}{3}+b+\dfrac{4}{3}=4  d'où b=0


\dfrac{8}{3}+0+\dfrac{4}{3}=4

Posté par
matheux14re : a , b et c 11-11-20 à 20:01

Oui , mais (C) ne passe pas par A..

Posté par
heklare : a , b et c 11-11-20 à 20:16

Le dernier calcul était écrit pour vous montrer que A appartenait bien à la courbe  équation de la courbe

y=\dfrac{4}{3}\times x+\dfrac{\frac{4}{3}}{x-1} qu'il est plus simple d'écrire

y=\dfrac{4x}{3}+\dfrac{4}{3(x-1)}

Si l'on donne à x la valeur 2 on a

y=\dfrac{4\times 2}{3}+\dfrac{4}{3(2-1)}=\dfrac{8}{3}+\dfrac{4}{3}=\dfrac{12}{3}=4

Le point de coordonnées (2~;~4) appartient à la courbe

maintenant en image 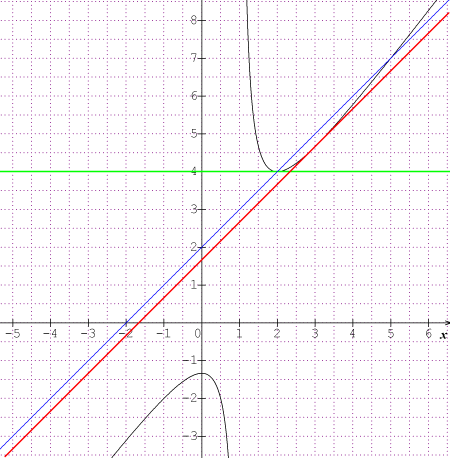a , b et c

en vert la tangente en 2  en rouge la tangente en 3 et  en bleu la droite donnée d'équation y=x+2

Posté par
matheux14re : a , b et c 11-11-20 à 21:12

Ah oui , j'avais mal saisi la fonction..

Merci


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1768 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !