salut
tout depend a quel ensemble appartiennent a et b.

explication.
a et b dans C.

b=0 alors a=0 et donc a=b=0.

b different de 0.

alors a^n=b^n <=> (a/b)^n = 1.

a/b est une racine n eme de l'unite.

il existe k dans [[0,n-1]] tel que a/b=e^(2*i*k*Pi/n)

et donc a=b*e^(2*i*k*Pi/n).

remarque : si a et b sont dans R, les seules racines n eme de l'unite dans R sont 1 et -1 (pour -1 si n est pair) si qui nous ramene a ta conclusion. et effectivement ton raisononnement est juste a condition d'etre dans l'ensemble des reels.
a+

Bonjour

Une petite remarque tout de même , ce n'est pas la bijectivité de qui fait la premiére équivalence mais juste l'injectivité


Jord

tout a fait Nightmare. c'est l'injectivite a elle seule qui nous permet de donner la premiere equivalence.

Merci !

Ah effectivement (je n'ai fait que survolé les notions d'injectivité et de surjectivité), et j'avais par ailleurs une petite question à ce sujet :

par définition une fonction f est injective lorsque pour tous reels
a et b de l'ensemble de départ,
f(a) = f(b) => a = b

Je pense avoir compris la signification mais je n'en suis pas certain, ce serait "f injective lorsque tout reel de qui par f admet un antécédent, n'en admet qu'un unique"
(c'est à dire , tout reel de l'ensemble d'arrivée admet 0 ou 1 antécédent)

Dans ce cas là une fonction strictement monotone est injective non ?

La surjectivité , si j'ai bien compris consisterait à dire que tout élément de l'ensemble d'arrivé admet (au moins) un antécédent, ce qui est d'apres le théoreme des valeurs intermédiaires, le cas pour les fonctions continues...

Donc en fait, lorsqu'en terminale on nous demande de montrer la stricte monotonie Et la continuité (pour montrer qu'une fonction est bijective) on nous fait étudier l'injectivité et la surjectivité de la fonction sans nous le dire ?

voila ce fut long :p
j'aimerai vraiment approfondir correctement ces notions qui me semblent indispensables pour la suite, alors si vous avez des conseils ou encore des liens ... merci

en me relisant je me rend compte que j'ai mis un mot de trop, il ne fallait pas lire "f injective lorsque tout reel de qui par f admet un antécédent" mais "f injective lorsque tout reel qui par f admet un antécédent" :p

Bonjour

Une application f est injective si tout élément de son ensemble d'arrivée admet au plus un antécédent f.

Toute fonction strictement monotone est injective : C'est même plus fort , elle est bijective

Une application g est surjective si tout élément de son ensemble d'arrivée admet au moin un antécédent par f

"ce qui est d'apres le théoreme des valeurs intermédiaires, le cas pour les fonctions continues"

Attention ! En effet , le théoréme nous indique que sur un intervalle [a;b] , quelque soit le k compris entre f(a) et f(b) il existe un antécédent de k par f appartenant à [a;b]
Mais rien ne nous indique que l'intervalle [f(a);f(b)] (ou [f(b);f(a)]) est toujours l'ensemble d'arrivée de f , loin de là !

Par exemple , on prend la fonction carrée , effectivement elle est surjective , mais seulement sur R+ . Mais par contre aucun réel de R- n'admet d'antécédent par cette fonction donc l'application carrée n'est pas surjective.

Par contre on peut énoncé le théoréme suivant :
Toute fonction f continue sur un intervalle I est une surjection de I sur f(I)
de même :
Tout fonction strictement f monotone sur un ouvert I est une bijection de I sur f(I)


Jord

Lorsque j'ai dit : " l'application carré est surjective sur R+" c'est un abus de language pour dire que c'est une surjection de R sur R+ et non pas que c'est une surjection de R+ sur un autre intervalle " .
Souvent lorsqu'on mentionne la "jectivité" (néologisme , à ne pas utiliser en devoir ) d'une application l'ensemble que l'on restreint est l'ensemble d'arrivée , c'est pour cela que lorsqu'on énonce des applications, on énoncé bien leur ensemble de définition ET leur ensemble d'arrivé (chose que l'on peut négliger lorsqu'on ne compte pas étudier la jectivité de l'application)


Jord

Il me parait étonnant qu'une fonction strictement croissante soit nécessairement bijective,
à moins que la stricte monotonie entraine la continuité implicitement ?
dans tous les cas pour montrer la bijectivité en Terminale du moins, on doit
étudier à la fois la stricte monotonie et la continuité.
(en tout cas c'est la premiere fois que je vois cela, dans tout les ouvrages que j'ai pu voir
on ne parle que d'injectivité dans le cas de fonction strictement monotones)

Tu prends ensuite l'exemple de la fonction carré, mais comment sait on que l'ensemble d'arrivé F
est R (et non R+) ? (donc qu'elle n'est pas surjective)

Enfin, j'ai toujours cru que lorsqu'on disait qu'une fonction etait surjective, injective ou bijective
sur un ensemble E , l'ensemble E représentait l'ensemble de départ
(cad par exemple que : f bijective sur E signifie que pour tout k€f(E), il existe c€E / f(c) = k , mais
apparement je me suis trompé Oo)

Bonjour,
"Il me parait étonnant qu'une fonction strictement croissante soit nécessairement bijective"
Attention, être bijectif est une propriété qui dépend des ensembles sur lesquels on défini la fonction. On est pas bijectif, mais on est bijectif de tel ensemble vers tel autre ensemble
La surjectivité n'est pas un problème, il suffit de se restreindre à l'ensemble des points qui sont atteints.

"à moins que la stricte monotonie entraine la continuité implicitement
Il n'y a pas vraiment de rapport direct entre continuité et bijectivité.
Cependant si une fonction réelle est strictement croissante, alors elle est presque partout continue. En fait elle est même mieux que ca, l'ensemble de ses points de discontinuités est dénombrable.


"Tu prends ensuite l'exemple de la fonction carré, mais comment sait on que l'ensemble d'arrivé F
est R (et non R+) ? (donc qu'elle n'est pas surjective)"
Justement ca dépend de l'ensemble d'arrivée que tu considères.

"Enfin, j'ai toujours cru que lorsqu'on disait qu'une fonction etait surjective, injective ou bijective
sur un ensemble E , l'ensemble E représentait l'ensemble de départ"
Oui en général c'est le cas, mais c'est une grosse faute de langage et on ne l'utilise que lorsque les esprits sont clairs.

A+

Merci otto d'avoir pris le relay

Pour compléter un peu l'histoire des ensembles de départ et d'arrivé.

Je ne sais pas si tu l'as déja fait, mais souvent, on note une fonction comme cela :


La plupart du temps , E représente l'ensemble de définition de f (on dit alors que f est une application). Autrement , E est restreint à un sous ensemble (on peut appeller cela application restreinte de f).
Mais malheureusement , au lycée en tout cas , la quasi totalité du temps , F est .
Du coup , les éléves n'étant pas habituer à vraiment toucher à l'ensemble d'arrivée, pour parler de bijection (car il ne me semble pas que l'on parle d'injection et de surjection au lycée), les profs on induit la notion de bijection (ou sur/injectiond'un ensemble sur un autre.
En effet, ça arrangeait tout.
Par exemple dans le cas de la fonction carré, on peut dire que c'est une surjection de sur .

Mais au lieu de cela , on peut aussi dire que l'application:
est une surjection (ou est surjective)
Et encore mieux si l'on restreint à :
est une bijection (ou est bijective)
ou encore :
est une injection (ou est injective)

Voila , d'où l'importance de bien parler des ensembles de départ et d'arrivé.


Jord

Je voudrais bien te donner un super site, mais j'arrive plus à trouver l'adresse.
Je te les donne comme ca alors, en faisant des copier collé.
Ok?

Injection

La fonction f est dite injective si deux éléments x et y de l'ensemble de départ ont toujours deux images distinces dans l'ensemble d'arrivée. Un bon exemple est le numéro de Sécurité Sociale : deux personnes ont toujours un numéro de Sécurité Sociale différent... La fonction qui à une personne associe son numéro de Sécurité Sociale est injective! En revanche, il existe plusieurs personnes qui sont nées un 06 février 1977. La fonction qui à une personne associe sa date de naissance n'est pas injective.

Mathématiquement, f est injective si pour tout x,y de E, f(x)=f(y) entraîne x=y. Quand les ensembles finis, il ne peut y avoir une injection de E dans F que si F a plus d'éléments que E. Un exemple très courant de fonctions injectives sont les fonctions de R dans R qui sont strictement croissantes!

Surjection

La fonction f est dite surjective si tout élément de l'ensemble d'arrivée (F) possède au moins un antécédent dans l'ensemble de départ (E), ie si pour tout y de F, il existe x de E avec y=f(x). Par exemple, si vous prenez un troupeau de vaches, la fonction qui à une patte associe la vache à qui cette patte appartient est surjective! En général, cela signifie que l'ensemble F est plus gros que l'ensemble E.
Et enfin,...

Bijection

La fonction f est dite bijective si elle est à la fois injective et surjective, ou encore si tout élément y de F possède un unique antécédent x par f dans E.
Un théorème couramment utilisé est qu'une fonction de R dans R strictement croissante réalise une bijection de R dans f(R).


Ayoub.

"Un théorème couramment utilisé est qu'une fonction de R dans R strictement croissante réalise une bijection de R dans f(R). "

Elle peut être strictement décroissante aussi . Donc sttrictement monotone serait plus approprié ici

Pour la surjection , toutes les applications f de E dans f(E) continues sont surjectives.


Jord

"Quand les ensembles finis, il ne peut y avoir une injection de E dans F que si F a plus d'éléments que E."

C'est vrai aussi si les ensembles sont infinis. En fait c'est ainsi que l'on construit la notion de cardinalité des ensembles infinis.

"toutes les applications f de E dans f(E) continues sont surjectives."

Pourquoi doit on être continu?
Toute application de f de E dans f(E) est surjective.

Oui c'est vrai je sais pas pourquoi

Il n'y a pas vraiment de rapport direct entre continuité et bijectivité.
Cependant si une fonction réelle est strictement croissante, alors elle est
presque partout continue. En fait elle est même mieux que ca, l'ensemble de ses points
de discontinuités est dénombrable.

Et si la fonction
f : E->F
    x->f(x)

n'est pas continue en un nombre fini de valeurs de E on ne peut pas dire que f est une
bijection de E dans F (comme elle n'est pas une surjection de E dans F puisque tout
point de F n'admet pas forcément un antécédent par f)

en effet :
Une fonction est une bijective si et seulement si elle est à la fois injective et surjective



Toute application de f de E dans f(E) est surjective.
est ce lié au fait que f(E) n'existerait pas (ou ne serait pas un intervalle du moins) si f n'était pas continue ?


PS : merci à toi 1 Schumi 1, je crois que j'avais dejà connaissance de ce site ^^

Désolé Nightmare si j'insiste lol (patapé )
mais j'ai encore le théoreme devant moi qui est clair :

Si est Continue et Strictement monotone sur un intervalle I de R,
alors f est une bijection de l'intervalle I sur l'intervalle f(I)
(de source sûre)

ou encore :

Si f est une fonction Continue et Strictement monotone sur [a;b] alors
f est une bijection de [a;b] sur [f(a);f(b)] ou [f(b);f(a)]
(bon vous me faites grace des limites lorsque a,b€{+oo,-oo} :p )


et la définition de la bijection que tout le monde connait :

une fonction f est bijective si et seulement si
tout élément de l'ensemble d'arrivée F admet par f un et un seul antécédent dans l'ensemble
de départ E.

on considere f :
[a;b]->[f(a);f(b)]
x->f(x)

et on suppose f strictement croissante sur [a;b] (d'apres otto, ce n'est pas génant si la fonction n'est pas continue en un nombre fini de points)

Ci joint une représentation graphique de f (avec une discontinuité représentée par les ] [ )

la fonction est injective, puisque tout réel de [f(a);f(b)] admet au plus 1 antécédent
dans [a;b].
Néanmoins elle n'est pas bijective, en effet tout réel de [f(a);f(b)]
n'admet pas un unique antécédent par f, puisque alpha n'a pas d'antécédent.

donc lorsque tu dis
"Un théorème couramment utilisé est qu'une fonction de R dans R strictement croissante réalise une bijection de R dans f(R).


il semble manquer la continuité (par ailleurs le 1er théoreme que j'ai cité plus haut est le meme que le tiens
sauf que I n'est pas forcément R, et qu'il y a bien la continuité).

Voila, désolé d'être lourd mais là je nage

Nil.

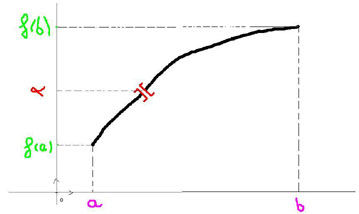
Par contre si F = [a;alpha[U]alpha,b] (= f([a;b]) ??? je suppose que c'est cela pour une fonction qui n'est pas continue ?)
je suis daccord avec vous lol

Exactement , rien ne précise que f([a;b]) doit être un intervalle .
Par exemple dans le cas de ta fonction ,

Mais tout élément de f([a;b]) admet bien un unique antécédent par f ( ne faisant par parti de f([a;b]) il ne pose pas de probléme)

Donc que la fonction soit continue ou pas le théoréme s'applique toujours


Jord

Je n'ai pas lu tout le développement (désolé si ca manque de respect) et je ne connais pas trop ton niveau, ni si tu cherches à t'informer où à répondre à une question scolaire, mais ce qui se dit dans ces dernieres interventions peut se généraliser par un théorème très important:

L'image d'un connexe de E par une application continue de E dans F est un connexe de F.

En très gros connexe = ensemble en un seul morceau.
En réalité il faut s'accorder sur ce que veut dire "un seul morceau" mais graphiquement on voit que ca représente quelque chose qui pourrait se tracer en un seul coup de crayon, et je pense que ce n'est pas sans rappeler une propriété vue en terminale ...
D'où le rapport entre fonctions continues et ensemble connexe.

A+

Daccord , voila qui est un peu plus claire dans mon esprit

Nightmare, je suis maintenant bien daccord sur le fait que ton théoreme s'applique :
"une fonction de R dans R strictement croissante réalise une bijection de R dans f(R)."

cependant, je ne vois pas de moyen direct pour déterminer f(R) sans passer par la continuité.
(dans tous les cas, à part graphiquement, je ne vois pas comment déterminer f(R) si jamais f n'est pas continue).


Par exemple si on voulait montrer la surjectivité de f en utilisant ce théoreme :
Toute application de f de E dans f(E) est surjective.

Il faudrait alors montrer que F=f(E) , encore faut il savoir trouver f(E)
(ce qu'on sait faire lorsque la fonction est continue)

PS : otto point de probleme, je ne sais pas si moi même j'aurai tout lu
Sinon mon niveau est celui d'un TS, et je cherche simplement à approfondir quelques notions hors programme Terminale, en vue d'une mpsi.

Re Nil

Ce n'est pas trés difficle de calculer l'image d'un intervalle par une application discontinue , la plupart du temps si on connait le point en lequel elle est discontinue , il suffit d'exclure son image de l'intervalle image.
Bon c'est pas trés clair ce que je dis , mais prenons par exemple une application qui est continue en tout point de sauf en 1

Pour calculer l'image de [0,2] par cette application , il suffit de calculer son image en supposant qu'elle est continue en 1 puis à priver l'intervalle image de l'image de 1 par l'application.

Ensuite pour ce qui est du :
"une fonction de R dans R strictement croissante réalise une bijection de R dans f(R)."
Je le répete encore , strictement monotone est mieux adapté.


Jord

Hum non en fait ma technique ne peut s'appliquer que dans le cas ou l'application est prolongeable par continuité au point ou elle est discontinue (ce qui est le cas de la fonction que tu as tracé) je retire donc ce que j'ai dit


Jord

En fait je viens de me rendre compte que ce n'est pas un cas de discontinuité que tu as tracé mais un cas ou tout simplement le réel qui a pour image n'appartient pas à l'ensemble de définition ...

>bonsoir NM

Mais si l'image de 1 est obtenue par un autre élément de [0;1[U]1;2] par l'application ?

J'ai loupé qqchose ?

Philoux

Non non , c'est juste le graphe de Nil qui m'a trompé , j'ai malencontrueusement mélanger discontinuité avec le simple fait d'appartenir à l'ensemble de définition.


Jord

ah, je vois :p
En même temps, si f n'est pas définie en une valeur, elle n'est pas non plus continue en cette valeur (donc c'est quand même un cas de discontinuité non ?)

désolé sinon j'ai quoté le théoreme avec "strictement croissante" sans faire gaffe, c'est bien sur strictement monotone que je voulais mettre.

Je pense que tout ceci m'a aidé a comprendre un peu mieux les notions touchant à la bijection, donc merci à vous. (tout n'est peut être pas clair à 100% mais maintenant c'est à moi d'aviser)

Par contre si vous avez des exemples d'exos qui les font intervenir je ne suis pas contre, car pour le moment je ne sais pas trop ce qu'on peut nous demander à ce sujet. (mis à part les "montrer que f(x)=k exactement 3 solutions" etc,... )

A+
Nil

Re

Tu peux t'amuser à montrer par exemple qu'il existe une injection de E dans F si et seulement s'il existe une surjection de F dans E


Jord

Pardons j'ai oublié de préciser que E et F étaient deux ensembles non vides