Bonjour,

ce n'est pas très difficile :

 Cliquez pour afficher

Bonjour,

 Cliquez pour afficher

Je trouve   un triangle  de cotés 66.15.23--->aire 14--->x=5

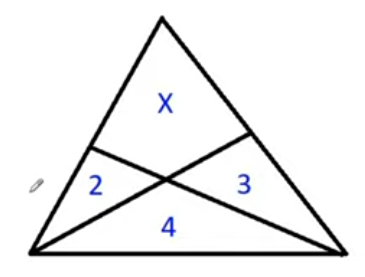
Bonjour dpi. Bon, ça me rassure de voir que je ne suis pas le seul à avoir galéré . Un indice en image pour un chemin possible vers la réponse. Vu la (bonne) réponse de jandri, ça n'est pas la seule voix, il a dû faire autrement.

 Cliquez pour afficher

En notant
Ne pas hésiter à faire apparaître les hauteurs issues de F qui disparaissent lorsqu'on fait le quotient  des aires:

On a: et

On tombe sur le système:
  -y+2x=3
4y-3x=6

et au final X=x+y=18/5+21/5=39/5=7,8

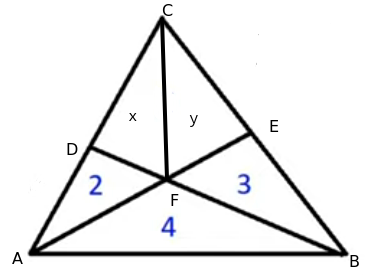
Bonjour fabo34,

j'ai partagé le quadrilatère par son autre diagonale, ce qui permet de calculer d'abord l'aire de la partie inférieure puis celle de la partie supérieure, on n'a ainsi pas besoin de résoudre un système

Bonjour à tous .

Je pensais avoir déjà posé ce problème ici mais je n'ai pas retrouvé sa trace

L'égalité d'aire proposé par Jandri n'est pas complètement évidente pour les jeunes :



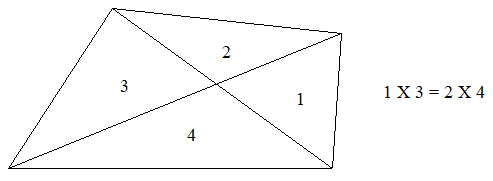
Il faudrait aussi expliquer comment obtenir la partie supérieure

Imod

Je me dévoue pour l'égalité d'aire. C'est le même principe que j'ai appliqué pour trouver mon système.

Par contre, la partie supérieure? Ca doit être tout bête, mais je séche

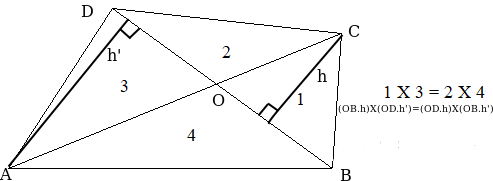
Je n'aime pas cette écriture (même si j'ai bien compris qu'il s'agit des aires des triangles).

Pour la partie supérieure c'est la même idée en considérant le point C sur le côté BE pour les triangles ABE et DBE (j'ai gardé les notations de la figure ci-dessus en notant E le point d'intersection des droites AD et BC).

En effet , vu comme ça c'est simple .

Imod

Même idée? Bon là il n'y a plus de quadrilatère comme ABCD et O l'intersection de ses diagonales.

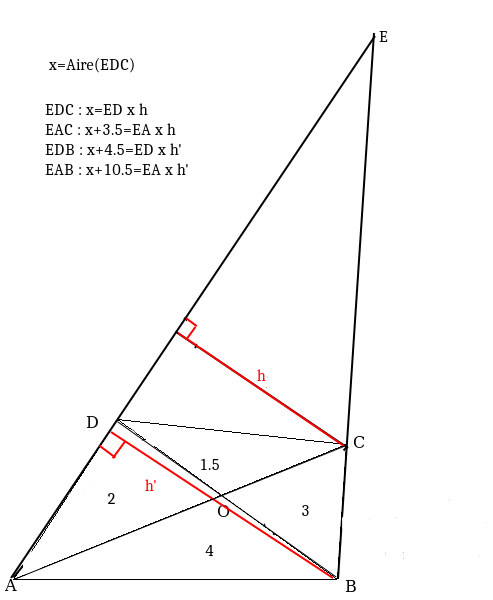
cf la figure où les valeurs numériques représentent les valeurs des aires connues. On a alors 4 équations. Pour supprimer les h, h', DE et AE, il faut faire les rapports. On obtient alors l'équation   , qui donne bien x=6.3

Tu confirmes pour la rédaction? Il me semble que tu pensais à quelquechose de plus immédiat.

En suivant les indications de Jandri on arrive directement à avec l'aire du triangle .

Imod

Je confirme

Comme je m'étais fourvoyé...
J'ai repris la méthode initiale de fabo34
(18/5)+(21/5)

dpi: tu devrais plutôt reprendre la méthode de Jandri, beaucoup plus belle!

jandri : oui bravo! Je cherchais un autre quadrilatère avec ses diagonales, mais en fait, cela fonctionne dans tous les cas. J'ai eu du mal à enlever mes œillères.
Pour dpi, je résume: 3 points alignés A,B,C et 2 points extérieurs E et D. Alors on a toujours:

    

Pour voir ça rapidement, on peut projeter orthogonalement E et D sur (AB) pour faire apparaître les hauteurs des triangles et en déduire les aires.

Imod: si tu m'avais écris ,  j'aurais trouvé plus vite . Avec les , je n'y comprenais plus rien; je cherchais un symétrique quelque part pour doubler l'aire

merci jandri pour cette élégante solution!

Avec un dessin pour indiquer au futur lecteur la solution la plus rapide (et la plus belle):

Bonjour,
Méthode bourrin, mais finalement pas si pénible :
Je choisis des coordonnées affines tells que A=(0,0), B=(2,0), F=(1,4), D=(x,6), E=(y,7). C=(z,t). J'écris les alignements : y=7/4, x=1/2, z=t/12 et finalement t=84/5 ; c'est l'aire totale du grand triangle, donc finalement l'aire manquante est 16,8-9=7,8

GBZM : bravo! Super idée. Ta méthode montre en plus qu'il y a une infinité de configurations possibles, chose à laquelle je n'avais même pas pensé!!

Effectivement, dans le cas général avec , alors les alignements BFD, AFE, ADC et BEC donnent les solutions suivantes:

Déjà, on voit que t est fixé:  

Ensuite,

Cette image avec 2 configurations suivantes:

illustre tes calculs

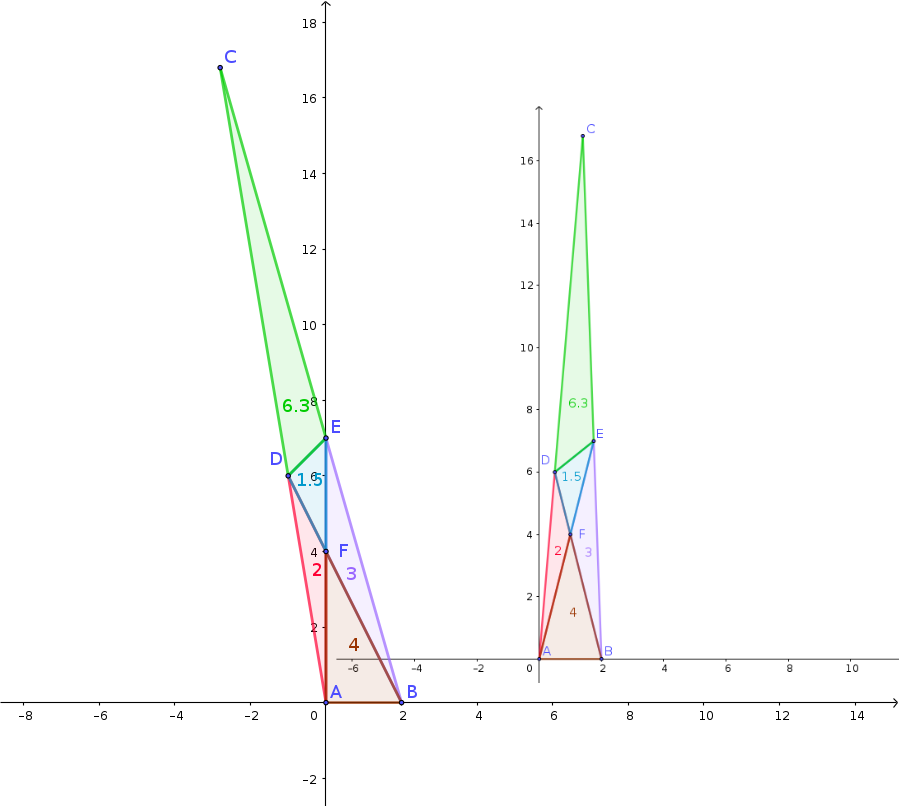
Pas d'accord. Il y a une seule configuration à transformation affine près. Il est donc totalement inutile d'introduire cette indéterminée .

ok. Ce sont les points A,B,D,E qui fixent les aires, et la translation de DE parallèlement à AB ne les changent pas.

Quand je parle de configuration, en fait c'est pour dire que ABF peut-être un triangle "quelconque" (aigu ou obtu) alors que le dessin initial de l'énigme montre un triangle aigu. Et que ma limitation d'esprit m'a fait pensé que fixer les aires "fixait" une unique figure. Surtout, je n'avais pas compris pourquoi tu pouvais fixer "arbitrairement" l'abscisse de F à 1, comme ça. Là je comprends mieux justement ce qu'il se passe après avoir fait varié ce , qui je te l'accorde est inutile. Mais peut-être d'autres pauvres âmes nulles comme moi seront-elles dans l'embarras ... avant de comprendre et de se dire: "mais oui, cétait évident!".

Ce n'est pas totalement évident. Quand j'ai écrit "Je choisis des coordonnées affines telles que A=(0,0), B=(2,0), F=(1,4)", j'ai utilisé le fait qu'étant donné trois points non alignés A, B, F, d'un plan affine P et trois points non alignés  S, T, U de R^2, il existe un unique isomorphisme affine de P sur R^2 qui envoie A sur S, B sur T et F sur U.

salut,
Les triangles A(0,0)B(b,0)C(c,168/(5b)) correspondent à la figure initiale de ce fil

C'est juste dire que l'aire du grand triangle est 16,8 (mon message du 02-09-23 à 11:20).

Bonjour,

on peut généraliser un peu cet exercice qui peut se résoudre avec les connaissances du collège : formule donnant l'aire d'un triangle (1/2 base fois hauteur) et équation du premier degré.

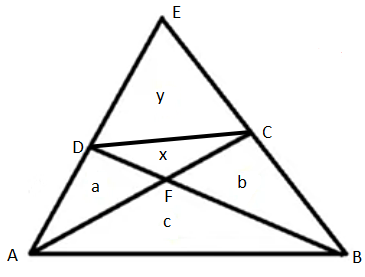
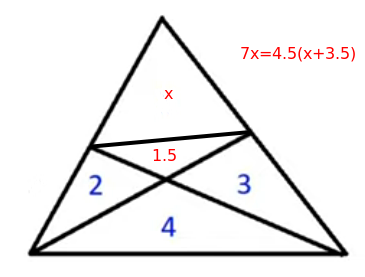
En remplaçant 2, 3 et 4 par a, b et c on obtient avec la formule donnant l'aire d'un triangle : (notation de la figure ci-dessous)

On montre avec cette même formule que qui est équivalent à .
Le cas enverrait le point à l'infini.

On obtient ensuite avec cette même formule et une équation du premier degré :

En calculant l'aire du grand triangle on peut alors remarquer que

Bonjour,
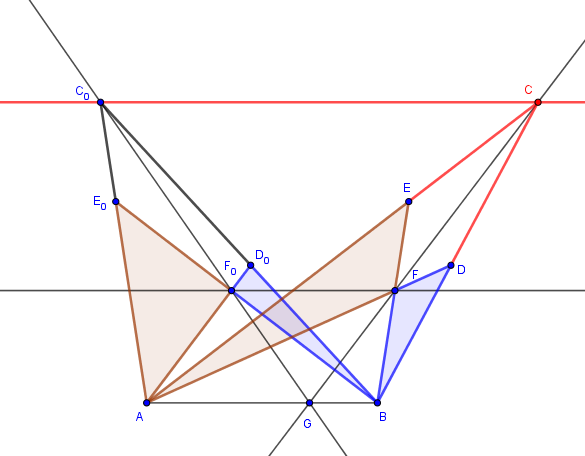
Juste un commentaire avec une figure (rien de bien nouveau) :

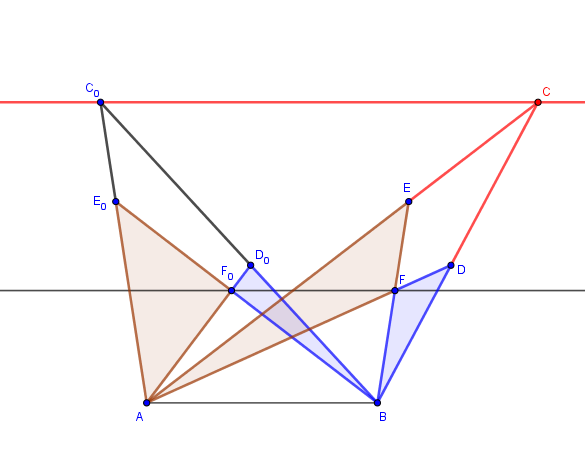
La figure générique : qui détermine les aires.
Le point décrit la parallèle à passant par en sorte que l'aire soit constante.
Le lieu de pour conserver les aires est la parallèle à passant par

Mince ! J'ai oublié le principal :

@lake : merci pour cette présicion. Ça reprend la bétise que j'ai écrite ( 02-09-23 à 20:54) lorsque je dis, avec tes notations, que la translation de parallèlement à ne change pas les aires. . Il faut évidemment rectifier avec ce que tu dis, à savoir:

Le lieu de pour conserver les aires est la parallèle à passant par !

Bonjour fabo34,
J'attendais ta réaction pour compléter la figure :



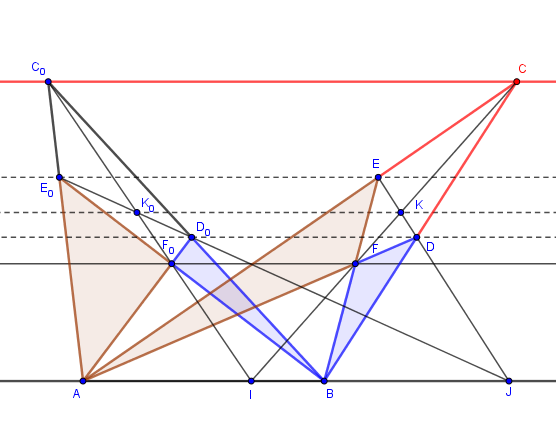
Dans cette configuration, les diagonales du quadrilatère passent par  deux points fixes de la droite :   et conjugués harmoniques par rapport à   et .

Ça va loin! je viens de vérifier, y'a un pavé la dessus sur wikipedia!