Inscription / Connexion Nouveau Sujet
Algo et equation
Bonjour... Un petit défi ?
On se donne deux entiers a et b choisis de façon aléatoire dans l 'ensemble {1,2,..100}
Quelle est la probabilité que l 'equation ax+by=39 ait des solutions dans Z ?
D'accord avec toi donc j'ai mal exprimé les critères:
1)il faut au moins un impair dans le couple (a,b)
2)il ne faut pas que a et b aient un diviseur commun exceptés 1,3,13.
3)je n'ai pas vu d'autres critères.
On observe plusieurs solutions pour les couples et quelques exceptions avec
une solution unique,exemple:
a=31 b=67 x=38 , y=-17 (1178-1139=39 )
Il n'y a jamais unicité de la solution , s'il y a au moins une solution
: par exemple tout couple de la forme
avec
est aussi solution.
Bonjour
Bravo à GBZM pour sa réponse rapide. Pour moi, cela n'a pas été immédiatement évident. On peut trouver une suite à ce problème. J'ai fait un petit programme qui donne le nombre de solutions suivant les limites qu'on s'impose pour x (et donc aussi pour y). Et, le nombre de solutions divisé par le nombre de cas testés semble tendre vers une limite d'environ 461.412. A quoi correspond cette limite si elle existe ? Je n'ai pas la solution.
Qu'appelles-tu "nombre de solutions" ?
Le problème de base est de compter les couples (a,b) d'entiers entre 1 et 100 tels que l'équation ax+by=39 ait une solution (x,y) en entiers relatifs.
Que comptes-tu maintenant ? Je n'arrive pas à comprendre ce que tu as écrit.
J'aimerais avoir la confirmation de 68.12 % de GBZM
En effet en refaisant le tour des cas a,b
*a ou b et a et b impairs--->25 % de cas sans solution.
*a et b sans diviseurs communs exceptés 1,3 et 13 .
*x ou y pouvant être négatif.
*On exclut uniquement les cas correspondants soit 84.
on obtient 2584 non-solution sur 10000 soit 74.16 %.
Tu peux fabriquer toi-me la confirmation en faisant tourner le code suivant sous python :
import numpy as np
compte=0
for a in range(1,101) :
for b in range(1,101) :
d=np.gcd(a,b)
if 39%d == 0 : compte+=1
compteCe code compte le nombre de couples (a,b) avec 1\leq a,b\leq 100 tels que le pgcd de a et b divise 39.
>derny
Il y a en effet de multiples solutions pour certains couples a,b mais combien trouves-tu
de non-solutions ,moi,je bloque à 2584.Merci 
Tu peux aussi (c'est plus pénible) utiliser un tableur.
Tu prépares un tableau 100x100 avec en indice de ligne (dans la colonne A) le nombres de 1 à 100 et en indice de colonne (dans la ligne 1 le nombres de 1 à 100. Tu as 10000 cases de B2 à CW101. Tu mets dans la case B2 la formule
=SI(MOD(39;PGCD(B$1;$A2))=0;1;0)
(moi j'ai LibreOffice, mais je pense qu'avec Excel c'est pareil)
et tu étends cette formule sur tout le tableau.
Il ne te reste plus qu'à faire la somme des 10000 cases du tableau. Et tu trouveras bien 6812.
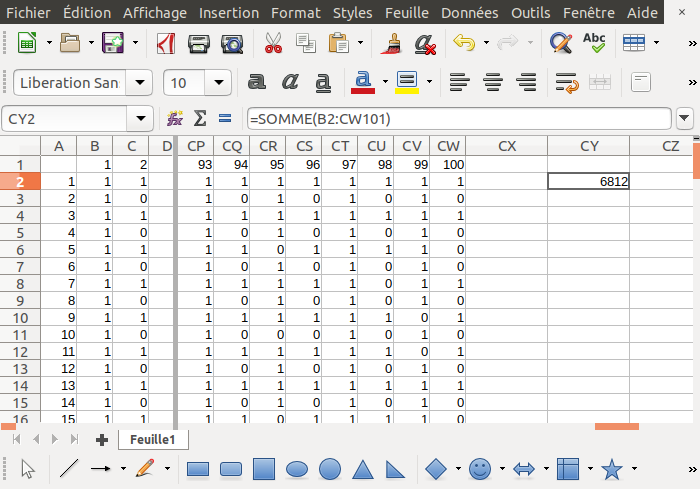
Je suis d'accord avec la réponse donnée (6812).
Comme le dit dpi, beaucoup de couples (a,b) ont beaucoup de solutions. C'est ce nombre de solutions divisé par le nombre de cas testés qui semble constant. Par exemple, si on limite x de 1 à 20000 on a 9227784 solutions pour 20 000cas testés. Si x varie de -9999 à 10000 on a 9228239 solutions pour 20000cas testés. Pour x de 1 à 100000 on a 46140085 solutions.
J'ai toujours un peu de mal à comprendre.
Tu comptes le nombre de quadruplets (a,b,x,y) tels que a et b sont compris entre 1 et 100, que x est compris par exemple entre 1 et 20 000, et ax+by=39 ?
C'est bien ça ?
Je me réponds moi-même. Je pense que c'est bien ça, à cause de ce petit calcul :
import numpy as np
compte=0
for a in range(1,101) :
for b in range(1,101) :
d=np.gcd(a,b)
if 39%d == 0 : compte+=d/b
comptedont le résultat (à peu près 461.4) colle à peu près avec ce que tu dis.
J'ai donné l'algorithme pour le calculer.
Peux tu comprendre d'après le code ?
Indication : si et
ont un pgcd
qui divise 39 et si
, alors les couples
solutions sont les
pour
.
Bonjour
A dpi : fais le tableau Excel préconisé par GBZM et tu verras tout de suite les cas impossibles.
A GBZM : merci pour tes compétences en programmation. On aura encore probablement besoin de tes services ainsi que ceux d'autres. Personnellement je ne programme qu'en Basic. Il serait temps que je me mette aux langages actuels bien plus performants mais j'ai du mal à trouver du temps. Je suis pris par d'autres problèmes et d'autres activités.
Je comprends les extensions d'un cas qui en donne une infinité d'autres. Mais je ne comprends pas (encore) le langage Python. Par contre je comprends les formules Excel (avec un peu d'effort tout de même pour certaines) et j'avais même commencé le VBA.
Quand j'augmente les valeurs de x, le nombre « 461.4 » semble tendre vers une limite. Peut-on trouver à quoi correspond cette limite ? C'était ça ma question en effet.
Je commente la procédure :
compte=0 # la variable compte est initialisée à 0
for a in range(1,101) : # a va de 1 à 100
for b in range(1,101) : # b va de 1 à 100
d=np.gcd(a,b) # d est le pgcd de a et b
if 39%d == 0 : compte+=d/b # si d divise 39, on ajoute d/b à compteAu final, on sort avec
J'ai donné une indication sur le pourquoi, dans le message ci-dessus. Pour rappel, quand le pgcd
La valeur exacte est :
>derny
Tu me connais assez bien pour savoir que j''ai commencè par ça.
Mon tableur ne donne pas de solution si a ou b ne sont pas impair (ou a et b).
Donc sur le 10000 possibilités il faut en exclure 2500.
Ensuite il ne me donne pas de solution si ils ont un diviseur commun excepté 1 ,3 et 13.
C'est là que je dois me planter car il n'y a que 84 cas ???
@dpi,
Pour les gens qui ne manient pas Python, j'ai expliqué en détail comment réaliser une feuille qui compte exactement les "bons" cas. À quoi ça sert que je me décarcasse ?
Si tu expliquais en détail ce que tu as fait avec ton tableur, peut-être pourrait-on voir ce qui cloche ? Mais là, que veux-tu qu'on te dise ?
Mon plus grand regret est de ne pas avoir appris à programmer avant 77 ans.
Par contre j'excelle sur Excel (voir le temps mis à résoudre la grille de mijo...)
j'ai mis en colonne a de 1 à 100 et b les impairs de 1à 99 (les pairs sont inutiles )
Je mets en variable x et y avec un facteur 1 ou -1 et j'obtiens toutes les solutions
ax+by = 39.
j'ai observé que les non-solution sont liées à a et b ayant un diviseur commun (autre que 1,3,13)
par exemple a= 20 b= 5 ou a= 51 b=27 soit 84 cas.
Bonsoir
dpi tu dis "exceptés 1, 3 et 13". Mais as-tu enlevé 3² par exemple ?
Merci à GBZM pour ces explications et son implication.
dpi je n'avais pas vu ton post. Pour a=51 et b=27 il y a des solutions. Pour a=20 et b=5 il ne peut pas y avoir de solutions car 39 n'est pas un multiple de 5 présent dans a et b.
Je ne comprends toujours pas ce que tu fais exactement dans ta feuille, mais j'ai bien l'impression que tu te compliques inutilement la vie.
Les entiers de la forme ax+by avec x,y entiers relatifs sont exactement les multiples du pgcd de a et b. C'est Monsieur Bezout qui nous dit ça. Les couples (a,b) pour lesquels il y a solution sont donc exactement ceux pour lesquels le pgcd de a et b divise 39,
Les couples (a,b) non solutions en dehors des (pairs, pairs), ça fait nettement plus que 84 ! Il y en a 688.
Dans ma feuille, les couples (a,b) non solutions correspondent aux cases où il y a 0.
Pour a=51 et b=27 il y a 2222solutions si on fait varier x de -10000 à 10000.
Comme je l'ai indiqué plus haut, la densité dans

 Cliquez pour afficher
Cliquez pour afficher


 ) et x et y dans
) et x et y dans 
 ).
).


