Bonjour,

la fonction est définie selon la syntaxe du langage utilisé pour programmer cet algorithme.

ne pas confondre algorithme : description formelle de l'enchainement abstrait des opérations
et programme : traduction d'un algorithme dans un langage donné, pour une machine donnée.

par exemple en Algobox (beurk, mébon) définir la fonction f(x) peut se faire dans l'onglet "utiliser une fonction numérique"
et alors la fonction f s'appelle F1 obligatoirement : SI (F1(c)>1) etc

dans d'autres langages on peut la définir par exemple par
function f(x) {
return x*x-3*x*ln(x)+1;
}


sur une calculette, lire la notice

etc

au pire tu remplaces directement f(c) par sa définition :

si (c*c-3*c*ln(c)+1 > 1) etc

c'est ici même le plus efficace, vu que la fonction n'est utilisée que dans cette seule et unique ligne de l'algorithme, on évite ainsi les "appels" de la fonction.
mais évidemment moins souple ! (si on veut changer de fonction par exemple, la définir "à part" est plus judicieux)

salut,
1/ quelle serie ?
2/ algorithme en langage naturel donc on peut utliser f(c)

série es

je pense que les reponses te satisfont ?

ben moi je pensais qu'un algorithme c'est un programme de calcul.

voici le 1er algorithme proposé qui ne convient pas.
j'essaie de comprendre pourquoi!?
initialisation

a prend la valeur 1

b prend la valeur 3

s prend la valeur 0
Traitement

n= (b−a)∗100
pour i allant de 1 à n faire
x prend la valeur a+0,01.i
s prend la valeur s+0,01.f(x)
fin de pour

sortie
afficher s


celui ci ne convient pas car rien ne dit que  n=(b-a).100  car on se limite aux centièmes pour les valeurs de x?
je ne comprends pas bien ce que calcule s.


merci

algorithme = "programme de calcul" certes
mais pas programme tout court.
il faut juste faire la différence entre un algorithme (un truc "abstrait", dans un langage abstrait dans lequel on écrit un peu avec une syntaxe "assez libre" par exemple "f(c)" tel quel dans se poser de question sur comment est définie f, sous entendue par l'énoncé)
et un programme (programme tout court) qui est destiné à tourner sur une machine physique et qui doit satisfaire à une syntaxe précise, à la virgule près, et dans lequel tout, absolument tout, doit être défini explicitement sans sous entendus.

pour ce nouvel algorithme :
Nota : ceci n'a aucun rapport avec le précédent algorithme et fonctionne lui aussi très bien...
donc cet algorithme "convient" (tout dépend à quoi bien sûr...)

combien de fois y a-t-il 0.01 dans b-a, dans l'intervalle [a; b] ?

l'algorithme calcule une valeur approchée de
(faire un dessin pour mieux voir ce que représente 0.01*f(x) comme aire d'un certain rectangle de largeur 0.01)

voici le dernier algorithme proposé pour déterminer une valeur approchée de f(x)=1

a prend la valeur 1

b prend la valeur 3


Traitement
Pour x allant de 1 à 3 faire
   .si f(x)<1 alors a prend la valeur (a+b)/2
   . sinon b  prend la valeur (a+b)/2
fin de pour

Sortie
Afficher a


je ne comprends pas bien ce que fait ce dernier algorithme

quant au premier je ne comprends pas bien pour quoi on affiche a quand b-a<0,01.

ce dernier algorithme par contre ne rime à rien.
la solution cherchée ne dépend pas que des valeurs de f pour x = 1, 2 et 3 et c'est tout dans le but de trouver une solution à 0.01 près !!!


"quant au premier je ne comprends pas bien pourquoi on affiche a quand b-a<0,01"
parce que tu n'as pas compris ce que fait vraiment cet algorithme

il s'appelle "recherche dichotomique"
il consiste à tester pour a et b variables (au départ 1 et 3) dans quel intervalle [a; c] ou [c; b] se trouve la solution, avec c milieu de l'intervalle [a; b]
(on coupe l'intervalle [a; b] en deux, d'où le nom "dichotomie")
on recommence ensuite en remplaçant la bonne borne a ou bien b (selon lequel des deux demi-intervalle contient x0) par c
et donc l'intervalle est réduit de moitié.

les deux bornes a et b à tout moment encadrent la solution cherchée (a < x0 < b) (on appelle ça un invariant de boucle)
la largeur de l'intervalle [a; b] diminue (est divisée par deux à chaque étape), on s'arrête quand cette longueur de l'intervalle [a; b] est plus petite que la précision demandée (0.01)

alors aussi bien a (que l'on décide d'afficher), que b d'ailleurs, est à moins de 0.01 de la solution cherchée x0 (qui reste inconnue en valeur exacte, on n'obtient qu'une valeur approchée à 0.01 près)

tel qu'il est écrit il ne fonctionne que si la fonction f(x) est monotone décroissante dans [1; 3] et que f(3) < 1 < f(1)
sinon il affichera n'importe quoi.
il faut donc s'assurer de cela au préalable (par un calcul numérique indépendant, étude de la fonction f(x), dérivée etc)


nota : donner dès le départ l'énoncé exact éviterait de comprendre toute cette discussion, de travers !!!

énoncé reconstitué par divination :
parmi les trois algorithmes suivants, lequel permet de résoudre f(x) = 1 à 0.01 près
suivent les trois algorithmes qui font donc partie d'un seul et même exo et pas de trois exos différents
d'ailleurs un exo de cette sorte aurait dû être mis à mon avis dans le niveau correspondant ("lycée" ? ou "supérieur" ?) en tant qu'exercice et pas comme question générale sur les algorithmes en général (le forum "autre")

d'accord je vais regarder tout ça merci

pour l'algorithme qui calcule l'intégrale
pourquoi calculer 0,01.f(x)?

l'algorithme calcule la somme des aires de tous les petits rectangles rouges comme celui là, chacun de largeur dx = 0.01



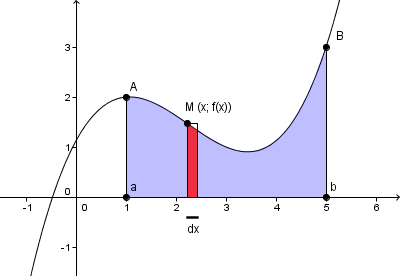
l'aire d'un rectangle de largeur 0.01 et de hauteur f(x) est 0.01*f(x)

on demandait juste de choisir parmi les 3 algos     et sans justifier !
Il suffit d'eliminer 2 des 3 algos.
le premier calcule une somme.
le troisieme n'evoque meme pas 0.01.
Mais c'est bien de vouloir comprendre ce que font les algos à eliminer.  (pas le jour du bac)

tout à fait mais je ne suis pas dans cette optique de choisir sans comprendre.
j'essaie de comprendre ce que fait chaque algorithme
c'est sans doute pour ça que je n'ai pas posté le sujet tel quel.
merci pour vos explications