Inscription / Connexion Nouveau Sujet
Analyse d'un graphe ?
bsr
notre projet c'est un GPS ultrasons(microphone et 5 hauts parleurs dans une salle
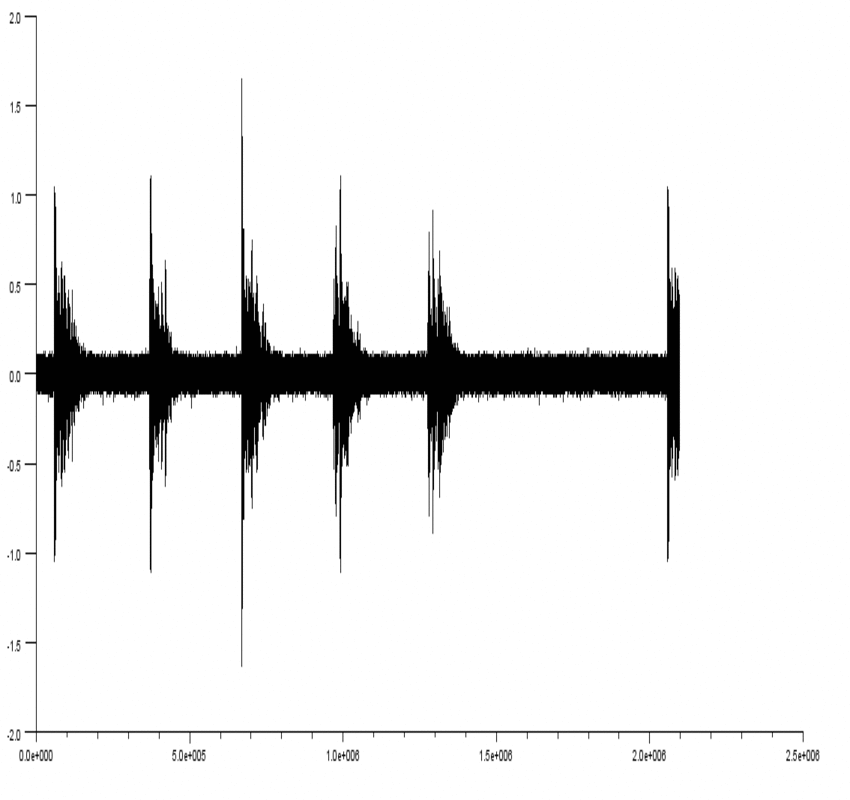
ces dernières sont fixé au plafond ). on a brancher le microphone avec un oscilloscope puis on a visualiser le signal et on a pris des points avec clé usb en fonctions du temps, puis on a programmer avec scilab ces points et on a obtenu ce graphe .
comment on peut savoir le point ou ce trouve le microphone par rapport ou hauts parleurs ??
dans le graphe on voie un signal puis une stabilité puis un signal .....
mercii
Bonsoir,
Quelques questions:
a) Quelle est l'unité de l'axe des abscisses du graphe ?
b) Les hauts-parleurs sont-ils actifs simultanément ? Si oui, sont-ils allumés à l'instant d'abscisse 0 sur le graphe ?
Cordialement.
J'aurais besoin de quelques précisions encore:
a) les unités des abscisses sont forcément une sous-unité de la seconde puisque l'on va jusqu'à 2,5 106. Sont-ce des ns (10-9 s) ?
106. Sont-ce des ns (10-9 s) ?
b) les hauts-parleurs semblent émettre par salves. La première salve est-elle émise à l'instant t = 0 sur le graphique ?
bsr
j'ai bien compris votre question
est ce que l'unité des abscisses la seconde ou bien la ns (10-9 s) ? c'est ca la question
mercii
Bonsoir,
Oui, c'est cela. Une unité en ns me parait assez logique car pour 2,5 106 cela ferait 2,5 ms et représenterait environ une distance de 80 cm pour une onde sonore. J'aimerais aussi savoir si tous les hauts-parleurs émettent leur salve en même temps et si cela se produit à l'instant t = 0 sur le graphique.
106 cela ferait 2,5 ms et représenterait environ une distance de 80 cm pour une onde sonore. J'aimerais aussi savoir si tous les hauts-parleurs émettent leur salve en même temps et si cela se produit à l'instant t = 0 sur le graphique.
bonjour,
j'ai demander au prof et il m'a répondu
a- l'unité c'est méga échantillon par seconde car c'est a la puissance 6 ( 2,5*106)
b-non, les hauts parleurs émissent pas à l'instant t=0
merci homeya
Je demeure perplexe car des méga-échantillons par seconde ne représentent pas, sauf erreur de ma part, une unité de temps. Les méga-échantillons par seconde ne seraient-ils pas associés avec l'axe des ordonnées (et non des abscisses) ? D'autre part, puisque les hauts-parleurs n'émettent pas à l'instant t=0, émettent-ils au moins en même temps leurs salves ?
Oui, en prenant les hypothèses suivantes:
a) les cinq hauts-parleurs émettent une salve en même temps
b) en se basant sur le temps de propagation des ondes sonores, le graphe permet de calculer à une constante près la distance entre le microphone et les cinq hauts-parleurs
Ensuite, on se définit:
a) un repère (ayant par exemple pour origine un des coins de la pièce)
b) on désigne par M(x;y;z) la position du microphone dans ce repère (x, y et z étant bien entendu inconnus)
c) on désigne par H1(x1;y1;z1) jusqu'à H5(x5;y5;z5) les positions des 5 microphones (toutes connues)
d) on désigne par d la distance entre le premier haut-parleur et le microphone (d inconnu) et par d+ , d+
, d+ , d+
, d+ et d+
et d+ les distances des hauts-parleurs 2, 3, 4 et 5 au microphone;
les distances des hauts-parleurs 2, 3, 4 et 5 au microphone;  ,
,  ,
,  et
et  peuvent se déduire du graphe et sont donc considérés comme connus.
peuvent se déduire du graphe et sont donc considérés comme connus.
A partir de là, on peut écrire le système:
 [(x-x1)2 + (y-y1)2 + (z-z1)] = d
[(x-x1)2 + (y-y1)2 + (z-z1)] = d
 [(x-x2)2 + (y-y2)2 + (z-z2)] = d+
[(x-x2)2 + (y-y2)2 + (z-z2)] = d+
 [(x-x3)2 + (y-y3)2 + (z-z3)] = d+
[(x-x3)2 + (y-y3)2 + (z-z3)] = d+
 [(x-x4)2 + (y-y4)2 + (z-z4)] = d+
[(x-x4)2 + (y-y4)2 + (z-z4)] = d+
 [(x-x5)2 + (y-y5)2 + (z-z5)] = d+
[(x-x5)2 + (y-y5)2 + (z-z5)] = d+
La résolution de ce système donnera les coordonnées de M (on pourra éventuellement choisir l'origine du repère dans un des coins du plafond ce qui amènera z1 = z2 = z3 = z4 = z5 = 0).


