Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques DétentePour discuter des JFF, des problèmes intéressants. ExercicesExercices ludiques [tout]Lister tous les topics de mathématiques
Niveau exercices
Autour d'une égalité de Ramanujan (III)
Posté par perroquet
Ramanujan avait proposé l'exercice suivant:
Dans un de ses cahiers, on trouve l'égalité suivante:
^2}+\root{3}\of{4(m-2n)(4m+n)}-\root{3}\of{2(m-2n)^2}\right|)
On se pose alors naturellement la question:
La réponse à cette question est négative (du moins si on impose que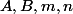 soient entiers).
soient entiers).
On trouve cependant ici le résultat suivant:
le résultat suivant:
On trouve dans le lien que j'ai donné la définition de "désimbriqué sur " et la démonstration, il y a un peu de théorie de Galois.
" et la démonstration, il y a un peu de théorie de Galois.
Curieusement, je n'ai pas trouvé de référence étudiant l'égalitém^3}{(4m+n)n^3})
lorsque Citation :
Montrer comment on peut "simplifier"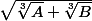 . En déduire que:
. En déduire que:
)
)
Montrer comment on peut "simplifier"
Dans un de ses cahiers, on trouve l'égalité suivante:
On se pose alors naturellement la question:
Citation :
Si on peut "simplifier"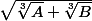 , peut-on trouver
, peut-on trouver 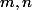 tels que:
tels que:
) et
et ) ?
?
Si on peut "simplifier"
La réponse à cette question est négative (du moins si on impose que
On trouve cependant ici
Citation :
Soit) deux rationnels non nuls tels que
deux rationnels non nuls tels que 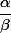 ne soit pas le cube d'un entier. Alors
ne soit pas le cube d'un entier. Alors 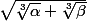 peut être désimbriqué sur
peut être désimbriqué sur  si et seulement si il existe des entiers
si et seulement si il existe des entiers 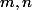 tels que
tels que
m^3}{(4m+n)n^3})
Soit
On trouve dans le lien que j'ai donné la définition de "désimbriqué sur
Curieusement, je n'ai pas trouvé de référence étudiant l'égalité
Bonjour,
la démonstration de la condition sur pour que
puisse être "désimbriqué" sur
n'est pas du tout du niveau terminale, en revanche la preuve de l'égalité de Ramanujan est très simple.
En développant on montre d'abord que
Ensuite on pose et
d'où
et
En remplaçant et
en fonction de
et
puis en prenant la racine carrée on obtient l'égalité de Ramanujan.


