Niveau autre

Calcul d'angles plans à partir d'angles dièdres

Posté par
arthropode 01-07-12 à 13:33

Bonjour,

A la fois pour moi, et à la fois pour réussir à faire le patron d'un polyèdre, je me pose la question suivante :
Comment calculer les angles au sommet à partir de trois angles dièdres ?

En plus concret, ça correspond à ça :
Soit un tétraèdre quelconque ABCS. On connaît les angles dièdres (entre deux faces) entre les faces ABS et BCS (nommons le ), BCS et CAS () et CAS et BCS (). En fonction de ces trois angles, comment exprimer les angles ASB, BSC et CSA ?

Je pense avoir trouvé une méthode :
- Trouver les vecteurs, , tels que les angles (;), (;) et(;) fassent respectivement , ,
- Puisque les angles dièdres sont égaux aux angles formés par les vecteurs normaux aux faces concernées, trouver les équations des plans normaux à (plan ABS), (plan BCS), et (plan CAS)*
- A partir de équations de plans, trouver l'équation des droites d'intersections des plans qui correspondant aux arrêtes de mon tétraèdre.
- Trouver les vecteurs directeurs à ces droites
- Enfin , sachant .=xx'+yy'+zz'=||||||||cos ASB, trouver les angles recherchés

J'étais bien parti en fixant mon premier vecteur (1;0;0), un deuxième (x;0;z) et mon troisième (x';y';z'), j'obtiens :
x=cos
z=sin
x'=cos
et c'est là que ça se complique :
z'= (cos-cos()cos())/sin()
y'= (sin²()-(cos-cos()cos())/sin())

A partir de là, j'ai réussi à avancer un petit peu, mais mes formules se compliquent tellement que cela devient impossible.
Connaissez vous un moyen de simplifier z' et y' ? Ou bien un autre moyen d'accéder à mes trois angles ? Sinon arrivez-vous à trouver ces angles malgré des formules de 3km de long ?

J'ai essayé d'être clair, mais si vous ne me comprenez pas, dites le moi, j'essaierai d'expliciter un peu plus.

Merci

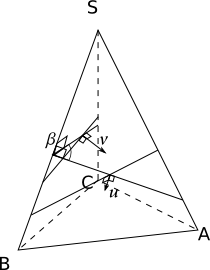
Posté par re : Calcul d'angles plans à partir d'angles dièdres 07-07-12 à 13:34

Pour ceux qui ne sont pas encore parti en vacances, je reformule mon problème avec un joli schéma et du LaTex.

Nous avons un tétraèdre quelconque SABC. En connaissant les angles dièdres (entre deux faces) entre les faces ASB et BSC (nommons le $\alpha$ ), BSC et CSA ( $\beta$ ) et CSA et ASB ( $\gamma$ ), comment trouver les angles $\widehat{ASB}$ , $\widehat{BSC}$ et $\widehat{CSA}$   ?

J'ai peut être trouvé un moyen :
Puisque l'angle dièdre formé par 2 plans est égal à l'angle formé par 2 vecteurs normaux à ces plans, il faut trouver 3 vecteurs $\vec{u}$ , $\vec{v}$ et $\vec{w}$ tel que les angle entre   $\vec{v}$ et $\vec{w}$ , $\vec{u}$ et $\vec{v}$ , et $\vec{u}$ et $\vec{w}$ fassent respectivement $\alpha$ , $\beta$ et $\gamma$ .

A partir de ces 3 vecteurs, on peut trouver l'équation des plans normaux à ces vecteurs (donc les plans ABS, BSC et CSA), puis les intersections de ces 3 plans, ce qui correspond à l'équation des arrêtes (AS), (BS) et (CS). Avec l'équation de ces arrêtes, il faut trouver  les vecteurs directeurs à ces arrêtes, puis avec les propriétés du produits scalaire, on peut trouver les angles recherchés.

Seulement, en faisant ça je trouve des expressions de plus en plus compliquées, au point de ne plus pouvoir continuer.

Posté par re : Calcul d'angles plans à partir d'angles dièdres 07-07-12 à 13:35

Voici l'image que j'ai oublié de poster

$Calcul d\'angles plans à partir d\'angles dièdres$

Posté par re : Calcul d'angles plans à partir d'angles dièdres 07-07-12 à 21:50

Bonjour,

Voir à "trigonométrie sphérique" sur Wikipédia par exemple pour les formules et même parfois des démonstrations

Centrons une sphère unité au sommet O = S du trièdre, A, B, C étant les traces sur cette sphère des arètes du trièdre.
Les longueurs des côtés du triangle sphérique sont tout bonnement les angles des arêtes.
Les angles aux sommets du triangle sphérique sont les angles dièdres !

Les notations sont celles de la figure de Wikipedia légèrement adaptées.
J'appelle A,B,C les angles appelés respectivement $\alpha, \beta, \gamma$ = angle des dièdres
et x, y, z les angles des arètes (= les arcs a, b, c de Wikipedia)

Soient $\vec{a} = \vec{OA}, \vec{b}, \vec{c}$ des vecteurs unitaires portés par les arêtes
L'angle des arêtes est $\cos x = \vec{a}.\vec{b}$ etc ou "." est le produit scalaire

$\vec{u} = \vec{a} \wedge \vec{b}$ est un vecteur perpendiculaire à la face définie par les vecteurs \vec{a}, \vec{b}
où $\wedge$ est le produit "vectoriel". Etc pour $\vec{v}, \vec{w}$ .
L'angle des faces est $\cos A = \frac{\vec{u}.\vec{v}}{|u| |v|}$ Etc

Calculons $\vec{u}.\vec{v} = (\vec{a} \wedge \vec{b}).(\vec{a} \wedge \vec{c}) = (|a||b|\sin z)(|a||c|\sin y) \cos A = \sin z \sin y \cos A$

Mais aussi :
$(\vec{a} \wedge \vec{b}).(\vec{a} \wedge \vec{c}) = \vec{a}.(\vec{b} \wedge ( \vec{a} \wedge \vec{c})) = \vec{a}.(\vec{a}(\vec{b}.\vec{c}) - \vec{c}(\vec{a}.\vec{b})) = (\vec{a}.\vec{a})(\vec{b}.\vec{c}) - (\vec{a}.\vec{c})(\vec{a}.\vec{b})$
(voir Wikipedia à "produit vectoriel" et/ou cours)

Ce qui donne $\cos x - \cos y \cos z$

Raté, j'obtiens $\cos A = \frac{\cos x - \cos y \cos z}{\sin y \sin z}$ ,
(A que je connais) en fonction des angles x, y, z (que je cherche)

Qu'à cela ne tienne, une méthode dans le même genre en sens inverse devrait aboutir aussi...

Si on part de $(\vec{a} \wedge \vec{b}) \wedge (\vec{b} \wedge \vec{c})$
qui est d'une part $\vec{u} \wedge \vec{v}$
et d'autre part en développant ce quadruple produit vectoriel : $((\vec{a} \wedge \vec{b}). \vec{c})\vec{b}$
C'est à dire un vecteur colinéaire à $\vec{b}$ et de module $\lbrack\vec{a}, \vec{b}, \vec{c}\rbrack$ , "produit triple" des vecteurs $\vec{a}, \vec{b}, \vec{c}$

Ceci permettrait de calculer $\vec{a}.\vec{b} = \cos z$ par la même méthode que celle utilisée ci dessus pour le calcul de $\vec{u}.\vec{v}$
et fournissant ce qu'on cherche.
En tenant compte soigneusement des signes et de l'ordre des vecteurs car le produit vectoriel est anticommutatif, et le produit mixte aussi

Je te fais confiance pour effectuer effectivement ces calculs jusqu'au bout, ou moyennant un changement d'échelle au facteur $\lbrack\vec{a}, \vec{b}, \vec{c}\rbrack$ près
décréter que c'est le même calcul, au signe près éventuellement, que celui effectué ci dessus et que on obtient effectivement, au signe près, la même formule que ci-dessus en échangeant le role de {A,B,C} et de {x,y,z}
(la difficulté est juste ce "au signe près")

J'espère ne pas avoir écrit trop d'aneries en recopiant tout ça en LaTeX, ou en me mélangeant les pinceaux dans tous ces vecteurs.

Cordialement.

Posté par re : Calcul d'angles plans à partir d'angles dièdres 09-07-12 à 09:43

Merci beaucoup.

Seulement, je ne sais pas utiliser les produits vectoriels, puisque jusqu'aux vacances, j'étais en première. J'ai donc un peu (beaucoup) de mal à suivre votre raisonnement.

Je peux par contre utiliser directement la formule $\cos c = \frac{\cos\gamma + \cos\alpha\,\cos\beta}{\sin\alpha\,\sin\beta}$ (), et tant pis pour la démonstration, même si j'aime bien connaître ce que j'utilise.

Mais encore merci pour votre réponse

Posté par re : Calcul d'angles plans à partir d'angles dièdres 09-07-12 à 11:48

Bonjour,

C'est vrai que j'avais fait un peu fort en parlant de produits vectoriels en Lycée !!
mais comme le niveau était marqué "Autre" et le problème plus pratique que scolaire...

Nota : la formule inverse (les angles dièdres à partir des angles des arêtes) s'obtient facilement sans produits vectoriels ni équations compliquées, avec juste quelques Al Kashi, Pythagore et relations trigo élémentaires. (7 lignes sur mon brouillon, en coupant le trièdre par un plan perpendiculaire à une arête)

La relation que tu cherches doit pouvoir s'obtenir en se triturant le cerveau pour voir dans l'espace "dual" où le role des arêtes est remplacé par des normales aux faces, en voyant bien que les normales aux plans définis par ces normales sont ... les arêtes !

Donc doit être aussi faisable de façon élémentaire (si on sait dessiner et voir dans l'espace)

Amicalement.

Posté par re : Calcul d'angles plans à partir d'angles dièdres 09-07-12 à 17:05

Re,

Voici la rédaction de la méthode "élémentaire" (sans calculs vectoriels).

Coupons le trièdre (O, ABC) par un plan perpendiculaire en M à l'arête OB
Définissant ainsi les points P et Q et les triangles rectangles OMP et OMQ
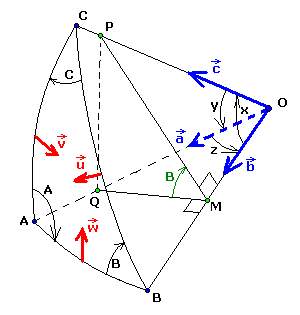
$Calcul d\'angles plans à partir d\'angles dièdres$
(les vecteurs et l'orientation sont pour justifier le calcul vectoriel précédent)
Prenons OM = 1
Dans le triangle OMP, OP = 1/cos(x) et MP = tan(x)
Dans le triangle OMQ, OQ = 1/cos(z) et MQ = tan(z)
Dans le triangle OPQ, Al Kashi donne PQ^2 = OP^2 + OQ^2 - 2.OP.OQ.cos(y)
Dans le triangle MPQ, PQ^2 = MP^2 + MQ^2 - 2MP.MQ.cos(B)

On en tire par substitution dans les deux valeurs égales de PQ^2 :
1/cos^2(x) + 1/cos^2(z) - 2cos(y)/(cos(x)cos(z)) = tan^2(x) + tan^2(z) - 2 cos(B)tan(x)tan(z)

Avec tan^2 = 1/cos^2 - 1, en regroupant les termes et en multipliant finalement par cos(x)cos(z)/2 :
cos(B)sin(x)sin(z) = cos(y) - cos(x)cos(z) ou encore :

cos(B) = (cos(y) - cos(x)cos(z)) / (sin(x)sin(z))

(si on retire les lignes de texte et les lignes blanches : 7 lignes de calcul, comme annoncé)
et respectivement par permutation circulaire donnant cos(C) et cos(A)

Nota : le plan MPQ est tangent à la sphère unité (de rayon OM) en M, assurant l'identité des angles dièdres (B) et des angles du triangle curviligne sur la sphère.

En sens inverse, cela est bien plus délicat.
On peut certes résoudre le système en x,y,z mais les calculs deviennent vite haabominaaables.

Il n'est pas très facile non plus de visualiser le trièdre "dual" défini par ses arêtes perpendiculaires aux faces du trièdre donné (directions des vecteurs u,v,w de la figure) et surtout de voir le lien étroit entre ces deux trièdres.
C'est pourtant la clé du problème.

Les arêtes du trièdre dual (= les normales aux faces du trièdre donné, = les vecteurs u,v,w) font des angles de X = 180 - A (resp. B,C)
Les normales aux faces du trièdre dual sont les arètes du trièdre donnés (si, si...)
Les angles dièdres du trièdre dual sont donc 180 - x (resp y, z)
On a donc en appliquant les formules précédentes au trièdre dual :

cos(180 - y) = (cos(180-B) - cos(180-A)cos(180-C)) / (sin(180-A)sin(180-C))
C'est à dire

cos(y) = (cos(B) + cos(A)cos(C)) / (sin(A)sin(C))

Et respectivement par permutation circulaire donnant z et x.

Avec un minimum de calcul.
(je n'ai pas écrit mes formules en LaTeX car c'est un peu ch...t à la main)

Cordialement.