Inscription / Connexion Nouveau Sujet
calcul d'optimisation
Bonjour
La figure ci-dessous représente un couloir
Quelle est la longueur maximale de la planche AB pouvant tourner dans la pièce sans frotter aux murs ? (On donnera une valeur approchée à 1 cm près)
J'aurais tendance à répondre 350 cm mais je pense que c'est plus subtil, s'agissant d'un problème d'olympiade.
Je pense qu'il faut trouver une expression de fonction numérique dont on étudie les variations, mais je ne vois pas comment l'exprimer.
Pouvez-vous m'aider svp ?
Merci par avance
Bonjour,
Une piste peut-être :
Si on considère le repère dont l'origine est le point situé à l'angle du couloir comme ceci :
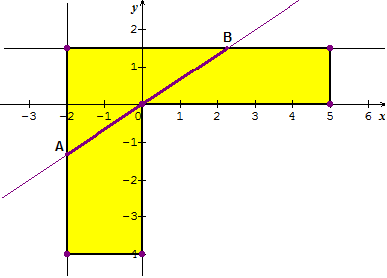
alors, il suffit de dire que la droite (AB) a pour équation y=ax.
Dans ces conditions, le point A a pour coordonnées (-2;-2a) et le point B(1,5/a;1,5).
Il suffit alors d'étudier la fonction distance(AB) en fonction de a et de minimiser cette fonction. Pour ma part, je trouve que le minimum est atteint pour a=0,9 environ, ce qui donne une longueur un peu inférieure à 5 (mètres)
Bonjour
j'ai repris l'exercice à partir de vos suggestions.
la dérivée première de la fonction distance (de la variable a, coeff directeur de la droite (AB)) a pour numérateur ;a étant strict positif (pente ascendante de la droite (AB)), ce polynôme s'annule sur
+ pour a 
0.909, donc je trouve à peu près comme vous, mais je trouve cette solution (le zéro positif) par résolution graphique ; vous, comment avez vous résolu l'équation ?
Donc je trouve une distance AB de 493 cm.
Mais je ne fais pas le lien, en tout cas pas clairement, car je pense que vous avez raison, entre MINIMISER la fonction distance et trouver la distance maximale qui permette de passer la planche.
Merci de me dire.
Mais je ne fais pas le lien, en tout cas pas clairement, car je pense que vous avez raison, entre MINIMISER la fonction distance et trouver la distance maximale qui permette de passer la planche.
Ca j'ai compris, c'est "logique", il suffit de réfléchir un peu...
Par contre je veux bien que vous m'indiquiez comment vous avez résolu l'équation de degré 4 ci-dessus.
je profite de ce message pour que vous me rappeliez svp (et je vais le noter une bonne fois pour toute dans mon formulaire) comment comment (syntaxe) on borne les valeurs en abscisses et en ordonnées sur les représentations graphiques de fonctions faites sur Sinequanon, dans l'interface de saisie des fonctions.
Merci
Bonjour,
Je me permets d'apporter ma modeste contribution :
Les exposants du numérateur sont 3 et 2 au début et pas 4 et 3 .
Par ailleurs les lettres A et B de la figure de patrice rabiller ne sont pas les extrémités de la planche ; ce sont les intersections avec les murs du couloir obtenues en prolongeant le segment qui représente la planche.
Il faut que la distance AB reste supérieure à la longueur de la planche pendant qu'elle pivote autour du coin, en glissant si nécessaire.
On cherche le minimum de la longueur AB. La longueur de la planche ne doit pas dépasser ce minimum, sinon elle se coincera.
Tu as trouvé tout seul pour le lien 
Pour l'équation, elle est de degré 3 et "a=0,9 environ" signifie je pense une résolution approchée.
Ton équation est bonne, elle est bien de degré 4.>> Alb12
remarquer que 16*x^4+12*x^3-12*x-9=(4*x+3)*(4*x^3-3)
Remarquable en effet, mais c'est surtout le fait que tu l'aies vu (d'autant que c'est avec les coefficients doublés) qui est remarquable.
Tu as des astuces pour "voir" ce genre de subtilités ? En tout cas
et merci pour ton intervention.
Merci aussi à Sylvieg..
L'astuce, c'est d'abord de ne pas se tromper dans le numérateur de la dérivée...
Ensuite, c'est de chercher si ce numérateur s'annule pour des valeurs simples ; et là, la calculatrice est utile !
Enfin il y a une propriété, qui n'est malheureusement plus au programme, qui permet de savoir que l'on peut factoriser par (x-a) si a annule le polynôme.
On trouve la factorisation par un moyen quelconque ; l'identification étant une possibilité.
16*x^4+12*x^3-12*x-9=(4*x+3)*(4*x^3-3)
vu la syntaxe c'est du Xcas 
Cependant la factorisation est evidente (brevet des colleges ? )
(16*x^4+12*x^3)-(12*x+9)= ...
J'arrive après la bataille ! Merci à ceux qui ont assuré le suivi du fil.
Je vais quand même répondre à la question posée concernant la syntaxe de Sine qua non :
je profite de ce message pour que vous me rappeliez svp (et je vais le noter une bonne fois pour toute dans mon formulaire) comment comment (syntaxe) on borne les valeurs en abscisses et en ordonnées sur les représentations graphiques de fonctions faites sur Sinequanon, dans l'interface de saisie des fonctions
Pour saisir une fonction sur un intervalle donné, on peut par exemple taper :
f1(x)=(3x-4)(x>-1)(x<=6) : fonction affine définie sur l'intervalle ]-1; 6]
f2(x)=(x²-5x+4)(x>=0) : fonction polynôme définie sur l'intervalle [0;+
[ . Au passage on remarque que le carré peut être obtenu en utilisant le caractère ² en haut à gauche du clavier. On peut aussi taper x*x ou x^2 ou même xx pour avoir le carré de x.
La syntaxe utilisée pour définir un intervalle est la même que celle employée sur les calculatrice Texas.
Pour obtenir une fonction définie sur 2 intervalles disjoints : on ne peut pas ! Il faut définir 2 fonctions différentes pour contourner cette difficulté. Le but de Sine qua non est de fournir un dessin : ce n'est pas un outil de calcul formel.
Bonjour
POUR PPA
Je me permets de vous poser la question suivante : est-ce un problème à résoudre sur le "papier" ou un "EXERCUE REEL" faire passer une planche dans un couloir ?
A bientôt
Je repasse sur le site et découvre que j'ai eu des réponses sur deux topics dont celui-ci, dont je n'ai pas été avisé par mail.....
>>M. Rabiller : merci pour ces rappels, que je note
>> Ma contribution : exercice tiré d'une Olympiade, mais allez savoir, je pourrais un jour être confronté à un problème de ce type....
Merci encore à tous/toutes les intervenant(e)s
Bonjour
Les Olympiades...... c'est excellent ......mais dans la réalité..... un "bon bricoleur" aurait passer une planche "plus longue" dans ce couloir.......sans même connaître PYTHAGORE.......
J'y ai aussi pensé alb 12 ; le problème est posé en dimension 2 alors que dans le réel on est en dimension 3. Ni la largeur de la planche, ni son épaisseur ne sont données, ni la hauteur sous plafond du couloir.
Il est assez rare d'avoir à faire passer une planche de 5 mètres dans un couloir ; par contre un sommier, une grosse commode ou un canapé c'est du vécu.
Bonjour
Je compatis avec SYLVIEG qui connait la dure réalité "d'un déménagement" et les problèmes mathématiques (et aussi de gros bras) qui se posent alors,
et je ne peux que la féliciter car
* elle connait "la réalité" d'une planche de bois qui peut prendre la dimension de 25 mm sur 27 mm et 6 000 mm de long (que l'on peut courber) et une planche de 75mm sur 225 mm et 6 000 de long (que l'on peut pas courber)
* elle sait que dans un couloir il y a des murs mais "aussi un plafond" et, là, notre ami PYTHAGORE est très utile.
Annuler
connectez vous