Inscription / Connexion Nouveau Sujet
calul d'une distance
Bonjour,
j'ai une point P(x,y,z) qui est dans un cube(dans l'image elle est en noir) ou je connus les position des coins de cube
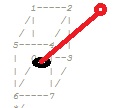
je veux la mettre en dehors de cube mon idée est
calculer la distance entre le point P est une face de cube ensuite déplacer P en utilisant cette distance
Problème; il y a 12 face , est ce que je dois calculer 12 distance et je sélecte la distance minimum?
ou je pense de calculer la distance entre point P et le point P1(qui est en dehors de cube
dist=p1-p2 si cette distance est positif c'est à dire je doit utiliser la distance entre P et la linge (coin4,coin7) sinon j'utilise la distance entre la ligne (5.6)
qu'est ce que vous pouvez me conseiller ?
le point P est à l'extérieur du cube si sa distance au centre du cube est supérieure strictement à la demi-diagonale du cube ....
en gros il est à l'extérieur de la boule de centre le centre du cube et de rayon la demi-diagonale puisque le cube est inscrit dans cette boule ...
Je n'ai pas bien compris ce que vous voulez me dire
Comme information la position de P se change toujours mais elle est dans le cube
je me suis trompé sur P peut-être ... mais bon ton énoncé n'est pas clair ...
je veux la mettre en dehors de cube
P est dans le cube je veux la mettre en dehors en utilisant la distance entre le points et les arrêts de cube et parce qu'il y a 12 arrêt je veux pas tout calculer j'ai fit que si.le point P1 et a droite de P je calcul que la distance entre P et l'arrêt droite si ion je calcul la distance entre P et l'arrêt gauche
Mon idée est de calculer les distances entre P et les arrêt de cube enduite utiliser la distance
minimal mais parce qu'il y a 12 arrêt la tache nnest pas facile
Alors je pense de travailler qu'avec 2 arrêt
Si point P1 est a droite de P je vais utiliser la distance entre P et l'arrêt droite sinon j'utiluse la distance entre P et l'arret gauche
En utilisant cette distance je peux mettre le point P en dehors en utilisant inertection de deux sphère
Si vous ne trouvez pas mon idée juste est ce que vous avez une autre idée
une condition suffisante est de prendre le maximum M des distances de P aux sommets du cube et de placer P1 extérieur à la boule de centre P et de rayon M ... ce qui me semble relativement simple ....
encore plus simple si c est le côté du cube il suffit de se placer à plus de 2c de P ....
Vous voulez dire le minimum et pas le max non ?
Et si j'utiluse cette solution je fait a chaque fois 9 test non ?y a pas un moyen pour minimiser le nombre de test
Pou la deudieme proposition si je déplace par 2c a quelle direction? Ou cnest juste j'utilise l'étape de cercle ou le rayon est 2c?
une condition suffisante est de prendre le maximum M des distances
vous voulez dire je calcule tout les distance entre P et les arrets et je prends la distance max ?
encore plus simple si c est le côté du cube il suffit de se placer à plus de 2c de P
mais quelle coté je dois tester
Et pour ma question de distance max?
Parce que peut je vais utiliser cette solution
La solution de M plus de 2c elle reste ambiguë je ne sais pas comment puis je la réaliser vous n'avez pas encore me répondre est ce sue je met juste un rayon de sphère =2 c ou quoi
Bonjour mielle, ton problème est hyper mal formulé.
On ne comprend pas ce que tu veux réellement.
Tu dis vouloir juste mettre P en dehors du cube.
Mais si ce n'était que cela, alors P étant à l'intérieur, il te suffirait d'ajouter ou retrancher "2c" à l'une quelconque de ses coordonnées pour obtenir un point P' forcément en dehors du cube (comme expliqué par carpediem).
En fait ajouter √3.c serait suffisant (car le plus long segment contenu dans un cube est sa grande diagonale qui vaut √3.c), et si le cube est orienté selon les axes de coordonnées, alors ajouter ou retrancher c suffirait.
Ton "vrai" problème est probablement plus complexe...
Mais sans énoncé, impossible de t'aider mieux.
merci beaucoup pour vos aides
pour le moment c'est ça mon problème , mais parce que je suis pas mathématicienne je trouve des problème surtout dans la géométrie malgré que la plupart des temps c'est problème sont trivial pour vous.
et oui je pense que √3.c est mieux parce que la nouvelle position et pas plus très loin de la position initial
juste une question trivial C : représente le centre d'une face quelconque ?
Oh , j'ai oublié
si P(x, y, z) est dans le cube alors M(x c, y c, z c) est hors du cube
je ne pense pas que travailler avec cette solution
parce que cette nouvelle point M ne garantie pas 100% que la distance entre MP1
c'est pour ça
je pense d'utiliser la distance maximal "dismax" , et je fait l'intersection entre le sphere de centre P et de rayan dismax et l'autre sphere de centre P1 et de rayon "distance entre PP1)
je pense c'est la solution ideal sinon :
je fait l'intersection entre sphere de centre P et de rayon (P+√3.c)et sphere de centre P et de rayan dismax et l'autre sphere de centre P1 et de rayon "distance entre PP1)
j'ai fait une erreur et parce que je ne peux pas modifier mon post je vais le mettre içi
c'est pour ça
je pense d'utiliser la distance maximal "dismax" , et je fait l'intersection entre le sphere de centre P et de rayan dismax et l'autre sphere de centre P1 et de rayon "distance entre PP1)
je pense c'est la solution ideal sinon :
je fait l'intersection entre sphere de centre P et de rayon (P+√3.c)et sphere sphere de centre P1 et de rayon "distance entre PP1)
un français très approximatif qui n'aide pas à la compréhension ....
désolé pour ma français , c'est pas ma langue native
mais j'essaye d'exprimer mon problème
je m'en doute
une remarque  3 < 2 donc P + 2c convient ....
3 < 2 donc P + 2c convient ....
par ailleurs c est le côté du cube .... voir à 19h53 ....
par ailleurs c est le côté du cube
OUI , je sais que c est le coté de cube mais mon problème est comment le calculer , parce que j'ai que les positions des coins , le coté de cube ce n'est pas une position , je me trompe ?
-----------------------
pour ma deuxième question est ce que je peux
utiliser la distance entre P et P+2c comme rayon de sphere et je fait l'intersection ? est ce que c'est juste ?
en faite je suis idiote , parce que j'ai un problème en français aussi j'ai pas bien compris ce que voulez dire par coté maintenant j'ai compris et je peux le calculé , en utilisant les coin d'une arrêt
-------------
il reste que ma question de
est ce que je peux
utiliser la distance entre P et P+2c comme rayon de sphere et je fait l'intersection ? est ce que c'est juste ?
Ok
je vais vous expléquer point par point
1- vous savez que P est liée par une autre point P1 , la distance entre les deux point est "dist"
2-lorsque je vais déplacer le point P endehors de cube avec 2C je dois garantir que la nouvelle position M est à distance "dist" de P1
3-la solution est de trouver l'intersection entre 2 sphere : sphere1 centre P , rayon "distance entre P et M"
sphere2 centre P1 et de rayon dist
je vais trouver une cercle , en fixons un coordonnée on va trouver les coordonnée désirer de M de telle sorte qu'elle est en dehors de cube et à la même distance de P1
est ce que vous m'avez compris maintenant ?

 c, y
c, y 
