Bonjour
le cercle de centre O inscrit dans le carré ne répond pas à la question ?
Et quel rapport avec le forum "enseignement" ?

Bonjour
Il s'agit de construire "l'autre" cercle bien sûr, dont le centre est compris entre A et O.
C'est la 1ère fois que j'utilise ce site, désolé si je ne suis pas sur le bon forum.

Tu as mis 'le' cercle, j'ai interprété 'un' cercle ... et finalement c'était 'les cercles' qu'il fallait comprendre ... donc tu ne lis pas les conseils avant de poster, et tu ne relis pas avant de poster ... c'est noté !

extrait de la FAQ du forum :

Q09 - Comment bien rédiger son message ?

Déjà, si vous lisez attentivement cette FAQ, c'est un bon signe.

Il est essentiel de respecter quelques règles lorsque vous rédigez votre message :

• Être poli : vous vous adressez à des êtres humains, pas à des robots qui résolvent des problèmes à longueur de journée. C'est pourquoi une politesse élémentaire se doit d'être respectée (bonjour, merci, etc.)


• Écrire en français et avec la qualité rédactionnelle requise : surveillez votre orthographe, et surtout évitez le langage SMS : rien n'est plus pénible pour un correcteur que de devoir décrypter un message incompréhensible ... A votre avis, s'il a le choix entre un message correctement écrit, bien présenté et une succession de caractères à décoder, privilégiera-t-il pour apporter son aide ?
  Il faut également souligner qu'écrire en majuscule donne l'impression de crier, évitez cela sur le forum. De même les successions de signes de ponctuation tels que " ! ! ! ! " donneront de vous une image très négative.


• Vérifiez votre énoncé : il ne faut pas qu'il reste des ambiguïtés dans l'interprétation de celui-ci. Si vous utilisez des fractions, assurez-vous d'utiliser le LaTeX pour représenter celles-ci, ou au pire d'utiliser des parenthèses. Comment les correcteurs pourraient deviner que x-1/x 2 signifie ou De même, rien n'est plus pénible pour un correcteur après avoir passé une demi-heure à vous aider dans l'étude d'une fonction de vous voir dire à la fin : " je me suis trompé dans l'énoncé, ce n'est pas la bonne fonction que j'ai écrit ". Mettez-vous une fois de plus à la place des correcteurs...

Avant d'envoyer définitivement votre message, pensez à vous relire une fois grâce à l'option aperçu qui est là pour cela.

Enfin, si vous obtenez une réponse, pensez à remercier la personne qui a donné de son temps pour essayer de vous aider, afin d'encourager les correcteurs à continuer à contribuer à faire vivre ce forum... Si ces correcteurs bénévoles passent du temps pour vous aider, et qu'ils n'obtiennent aucun signe de satisfaction et de reconnaissance du travail qu'ils fournissent, ils risquent bien de ne pas vous corriger la prochaine fois que vous aurez besoin d'eux...

extrait de la FAQ du forum :

Q12 - Dois-je forcément indiquer mon niveau lorsque je poste un nouveau sujet ?

Oui, indiquer son niveau (dans son profil) et celui du problème est obligatoire lorsqu'on pose une question.

Un correcteur pourra ainsi facilement juger s'il est en mesure de vous aider ou non. En l'absence de cette précision, aussi bien sur votre profil que sur le forum dans lequel le sujet est publié, il risque moins de vous indiquer une méthode que vous n'avez pas encore vue en classe, etc.

De même, si vous êtes élèves dans un pays francophone, vous pouvez consulter les équivalences des systèmes de niveaux scolaires afin de choisir le niveau de la classe française correspondant à votre classe. Cela permet au correcteur d'intégrer le fait que votre niveau scolaire ne correspond pas forcément à celui stipulé dans les programmes français en vigueur.

Il est de même demandé aux aidants de renseigner leur profil, ce qui en général donne une bonne indication du niveau de l'aide apportée.

Bon, je vois que là aussi, c'est compliqué. J'attendais une réponse à un problème, et j'ai des trucs du genre "réponse d'un prof à un élève".
Je me désabonne donc et je ne dis pas "à plus".

bonjour,

dommage, le problème était à priori intéressant, une fois formulé correctement
Il y a même trois cercles solutions
- le cercle de centre O déja cité, inscrit dans le carré
- le cercle cherché dont le centre est entre A et O
- et le troisième extérieur de centre au dela de O : tangent aux côtés (AB) etc ça veut dire aux droites (AB) et pas aux segments [AB] etc)


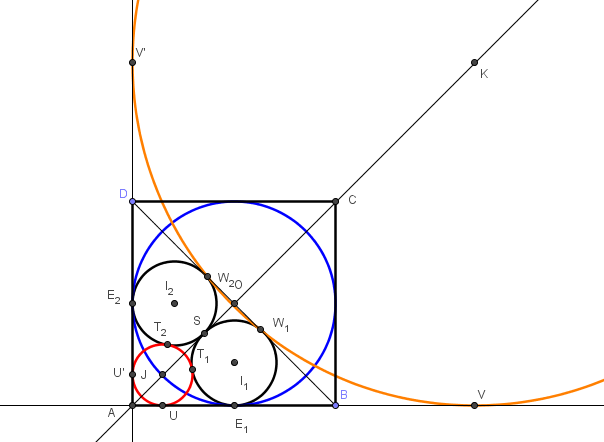
(attention le centre J du cercle rouge solution n'est pas sur le cercle bleu inscrit dans le carré)
construction classique avec les "problèmes d'Apollonius" : les 10 problèmes célèbres de cercles tangents à 3 cercles/points/droites donnés.
ici tangents à (AB), (AD) et (C1) cas "DDC" droite/droite/cercle (en ne gardant que ceux centrés sur la diagonale (AC) et donc forcément tangents à C2 par symétrie)

mais bon, si on ne dit pas le cadre / niveau / profil dans lequel on cherche un problème, c'est bien pris pour un exo à faire par un élève, c'est sûr
donc ne pas s'étonner qu'on réponde comme à un élève...
prendre ça ainsi en se barrant direct est faire preuve d'une vraie maturité d'esprit ...

joli ...