Inscription / Connexion Nouveau Sujet
Challenge n°119

Bonsoir, nouvelle énigme :
Les distances fournies sont en mètres.
Un minimum d'explications claires sur le raisonnement est exigé.
* image externe expirée *
Bonne chance à tous.


 Bonjour,
Bonjour,
le robot doit être sur la médiatrice de BD
il doit être à égale distance de A, B et D
calcul de BD = 1.5+0.67=2.17 => médiatrice à 1.085 de B
A est à (5.1-4.2)=0.9 sous B donc à 1.085-0.9=0.185 de la médiatrice
le robot est à x de la verticale passant en A tel que
0.185²+x²=(1.8-x)²+1.085²
x=4383/36 = 1.2175 m
donc le robot est sur une horizontale à 1.085 m sous B et sur une verticale à 1.2175 m à droite de A
En expérant avoir été assez clair et que ce soit bon 
Le WE n'attend pas... je n'ai pas le temps de vérifier...
Bon WE à ceux qui liront !
Philoux
 traçons le triangle ABD
traçons le triangle ABD
nous savons que C appartient au cotê BD de ABD
alors si on trace le cercle circonstruit du triangle
je pense que son origine sera me point le plus proche à la foit à A, B, C et D
 bonjour,
bonjour,
la premiere condition est la rotation maxi de 180° donc cela oblige a positionner le bras robotise sur AD ou AB .
sur AD on obtient des longueurs inferieurs a 1 metre donc pas possible
sur AB la position sera le milieu de AB puisque AB = 2,013 m
soit M ce point : MA=MB = 1,007 m > 1 m
MD=1,941 m
MC=1,383 m
dans un systeme ou DB est l'axe des x et la perpendiculaire issu de D l'axe des y (vers la gauche de votre dessin)
les coordonnees de M sont: {1,72 ; 0,90}
le bras de rotation est positionne au milieu de AB
j'espere que c'est bon
merci pour cette enigme
a la prochaine
Paulo
Je ne suis pas sûr de bien avoir compris le problème et ses hypothèses, mais j'ai voulu tout de même participer à cette énigme.
Simplement je demanderai à ne pas être noté (smiley ou poisson) car je ne suis pas du tout « satisfait » de ma solution qui utilise un logiciel de tracé et de calcul (Déclic : logiciel gratuit). Pour moi, une énigme, qu'elle soit en rapport avec un problème concret ou théorique, doit faire appel principalement à la réflexion et à un minimum d'outil. Ici, j'ai eu l'impression de faire du tracé sur papier millimétré et de la simple mesure au double décimètre !!!
Mais comme je l'ai dit, je suis peut-être passé à côté du problème !!
En effet :
1. il était illusoire de trouver les coordonnées du point directement en dérivant par exemple la fonction de deux variables f(x,y) = somme des distances. On ne pouvait que « voir » où il se trouve approximativement les points cherchés possibles avec un schéma.
2. le calcul des coordonnées des points possibles nécessitait le calcul de l'équation de cercles, de droites et celui de leur intersection.
3. enfin , le calcul des distances par  (x2+y2), et ceci en plusieurs points pour comparer les sommes était monstrueux !!
(x2+y2), et ceci en plusieurs points pour comparer les sommes était monstrueux !!
Bref, je crois être passé à côté , où alors puiséa a été très très dur avec nous !!! A mon sens, c'est le problème le plus « difficile » et le plus « calculatoire » depuis plusieurs mois, si on veut le résoudre analytiquement, donc précisément.
Voila ma solution et mon schéma obtenus après plusieurs heures :
L'énoncé nous dit que le bras a un angle maximal de 180°. Il ne peut donc se situer à l'intérieur du triangle ABD. De plus, il doit se trouver sur un cercle ou une droite délimitant les zones interdites et permises.
La figure est à l'échelle 3. Les cercles en réalité de rayon 1 ont un rayon marqué 3 sur la figure et toutes les distances inscrites sont donc à diviser par 3.
J'ai considéré que le problème consistait à calculer le point dont la somme des distances aux points A, B C et D était minimale, ce qui n'était pas précisé !!!
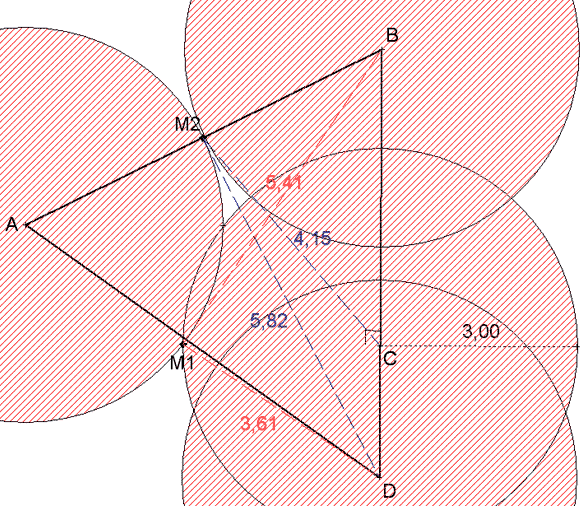
Le point M1 intersection des cercles de centre A et C, donne :
A : 1,00m
B : 1,80m
C : 1,00m
D : 1,20m
Soit un total de 5,00 m
Le point M2, intersection de la droite AB et du cercle de centre A donne :
A : 1,00m
B : 1,01m
C : 1,38m
D : 1,94m
Soit un total de 5,33 m.
C'est donc le point M1 qui est le point à « somme des distances minimale ».
Il faut donc placer le bras articulé à l'intersection des cercles de centre A et C (extérieure au triangle ABD). La distance aux 4 points est alors :
A : 1,00m
B : 1,80m
C : 1,00m
D : 1,20m
 La question n'est pas très claire (que veut dire: au plus près de ces quatre points? j'ai supposé que l'on cherchait le point tel que la somme des distances aux 4 points A,B,C,D soit minimale) mais on va essayer d'y répondre!
La question n'est pas très claire (que veut dire: au plus près de ces quatre points? j'ai supposé que l'on cherchait le point tel que la somme des distances aux 4 points A,B,C,D soit minimale) mais on va essayer d'y répondre!
Pour pouvoir fonctionner, le bras doit être situé à au moins 1m de chacun des points A, B, C, D. On peut calculer les distances suivantes AB=2,01m, AC=1,89m et AD=2,20m
Sur les 4 cercles de rayon 1 de centres ces 4 points, celui de centre C est sécant avec les trois autres, tandis que celui de centre A est disjoint avec ceux de centre B et D.
L'ensemble des points extérieurs aux 4 cercles, situés "au plus près des 4 points" se décompose donc en deux régions: une entre les cercles de centre A et D, l'autre entre les cercles de centre A et B.
Les points d'intersection M et N des cercles de centre A et C sont situés sur les parallèles à LN passant respectivement par A et C (puisque (1,8-1)^2+(5,7-5,1)^2=1)
On peut donc calculer MB=1,20m et MD=1,44m ainsi que NB=1,80m et ND=1,20m
Un rapide calcul montre que lorsque P parcourt le cercle de centre C en s'éloignant de M, à l'extérieur du cercle de centre A, la somme des distances PA+PB+PD augmente
Le point M est donc le point cherché et l'on a MA=MC=1m, MB=1,2m et MD=1,44m
 Bonjour
Bonjour
Le point P cherché est dans le triangle ABC. P est à 1 mètre de A sur la perpendiculaire en A à AL. De cette position, P se trouve à soit environ 1.204 mètre de B, à 1 mètre de C et à
soit environ 1.501 mètre de D.


 je pense qu'il doit etre au milieu du segment [AD]
je pense qu'il doit etre au milieu du segment [AD]
 je crois que je me suis tromper dans un nom :le centre du cercle circonscrit
je crois que je me suis tromper dans un nom :le centre du cercle circonscrit
voilà


 Bonsoir,
Bonsoir,
Petit problème de lieu géométrique sous certaines contraintes joliment emballé.
Sauf erreur, l'énoncé me parait incomplet: On peut facilement prouver (avec les distances données) que (EB)(EF) mais on ne sait rien sur (LA)...
Supposons que (LA)(LE) (sinon il est impossible de répondre!) même si la capture d'écran de géoplan semble indiquée le contraire !
L'idée des médiatrices est à écarter d'emblée. Tout d'abord la rotation maximum de 180° interdit de placer le bras à l'intérieur du triangle ABD même si la condition du minimum d'un mètre laissait une petite possibilité...
Je note I le point d'ancrage du bras.
Sous ces deux contraintes (1m et 180°), I doit minimiser l'ensemble Sup{IA,IB,IC,ID/IA1,IB
1,IC
1,ID
1}. Une figure laisse supposer que le point I cherché correspond à l'intersection des cercles de rayon 1 et de centres A et C (l'autre candidat milieu de [AB] s'avère être (après vérification) trop éloigné de D).
En se plaçant dans le repère (o.n.) de centre C, les coordonnées des points utiles sont A(-1,8;0,6), B(0;1,5) et D(0;-0,67).
Le cercle C(A,1) a pour équation (x+1,8)²+(y-0,6)²=1 et le cercle C(C,1) x²+y²=1. Ces deux cercles se coupent selon une abscisse x vérifiant 10x²+18x+8=0, ce qui laisse deux possibilités : x=-1 ou x=-4/5 mais la seconde (intérieure au triangle) est à exclure.
Le point recherché est donc le point I(-1,0).
Reste à calculer les distances manquantes.
IB= et ID=
Conclusion: Il faut positionner le bras robotisé à des distances (approximatives) respectives des points A,B,C,D de ,
,
et
(et dans le même plan que ABC)
Merci pour l'énigme.
Remarque: JFF, sans la condition des 180°, la solution plane donnerait une ditance ID de 1,5m alors qu'une solution dans l'espace permettrait de rogner encore un peu. En plaçant le bras sur la droite intersection des plans médiateurs à environ 0,7m du plan ABC, il est possible d'obtenir une distance maximale d'environ 1,41 (pour A,B et D) 


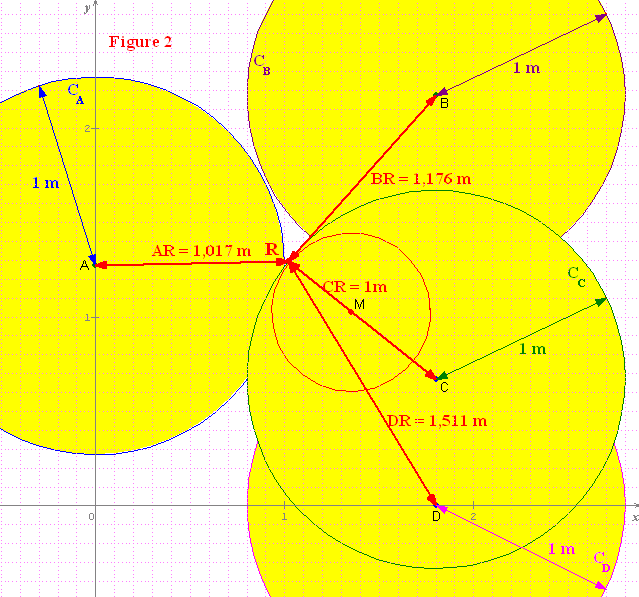
 Bonjour,
Bonjour,
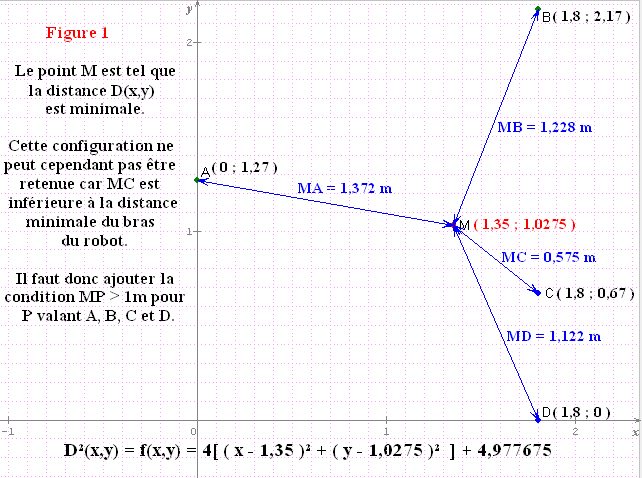
Le net m'étant accessible, je reposte après plus de temps de réflexion.
Je détermine un repère de centre O dans lequel les 4 points ont pour coordonnées :
A ( 0 ; 1,27 ), B( 1,8 ; 2,17 ), C( 1,8 ; 0,67 ) et D( 1,8 ; 0 ) ( cf. figure 1 )
L'information (E) : "... le bras motorisé [est] au plus près de ces quatres points..." peux se traduire en déterminant le point M(x,y) tel que AM²+BM²+CM²+DM² soit minimal.
D²(x,y) = f(x,y) = x²+(y-1,27)²+(x-1,8)²+(y-2,17)²+(x-1,8)²+(y-0,67)²+(x-1,8)²+y²
f(x,y) = 4( (x-1,35)² + (y-1,0275)² )+4,977675
f(x,y) sera minimale en valant 4,977675 pour x=1,35 et y=1,0275
le point M( 1,35 ; 1,0275 ) est optimisé; le calcul des distances se fait par Pythagore :
MA = 1,372 m ; MB = 1,228 m ; MC = 0,575 m ; MD = 1,122 m
En relisant l'énoncé, je m'aperçois que l'énoncé est incomplet car il ne dit pas comment se situe le robot dans l'axe vertical : est-il à la même hauteur que les quatre points ?
En supposant que le robot soit à la même hauteur que les points, on ne peut donc pas retenir la solution ci-dessus car le point M est à moins d'un mètre du point C, et donc l'information (E) : "longueur minimal du bras = 1m" n'est pas respectée.
Dans ce cas, portons les distances minimales interdites par des cercles colorés (cf. figure 2 du post suivant).
Ce sont des cercles de rayon 1m centrés sur chacun des points A, B C et D; ces cercles sont colorés en jaune => les zones possibles pour M sont laissées en blanc.
De D²=4( (x-1,35)²+(y-1,0275)²)+4,977675, on tire (x-1,35)² + (y-1,0275)² = D²/4 - 1,24441875
qui est l'équation d'un cercle centré en M trouvé précédemment et de rayon V(D²/4 - 1,24441875).
C'est donc une famille de cercles concentriques en M.
Il suffit de trouver le cercle le plus petit qui fournisse un point situé en zone blanche : ce point ne peut être que celui à la tangence des cercles de centres M et C.
en ce point R, les deux cercles sont tangents => C, M et R sont alignés => R est à l'intersection de la droite CM et du cercle C(C)
Droite CM : (y-0,67)(1,8-1,35)=(x-1,8)(0,67-1,0275) => y-0,67 = (-143/300)(x-1,8)=k(x-1,8) que l'on reporte dans C(C)
Cercle C(C) : (x-1,8)²+(y-0,67)²=1 => (x-1,8)²+k²(x-1,8)²=(1+k²)(x-1,8)²=1 => x=1,8-(1/(1+k²))^(1/2)
x=1,8-180/V52849 et y=0,67+143/V52849
donc R : x=1,017m et y=1,292 m
d'où les distances demandées, par Pythagore :
AR = 1,01725 m - BR= 1,17639 m - CR = 1 m (juste) DR=1,51077 m (valeurs approchées)
On peut également vérifier que le point à l'intersection des cercles de centre A et C ne fournit pas une distance D² minimale (5,7029 m² au lieu de 5,7010 m² pour R) => la distance AR=1m est à rejeter.
En espérant ne pas avoir fait d'autres erreurs de calcul ou de raisonnement...
Très beau problème dégoté par puiséa.
Dommage que l'incertitude de l'énoncé doit (devrait, logiquement) tolérer les valeurs trouvées plus haut puisqu'il n'est en aucun cas dit, dans l'énoncé, que le bras du robot est à la même hauteur que le point C :
C
/!
/ !
/ !
/ !
/ !
/ !
/ !
/ !
M-----------H avec MH = 0,575 m et MC = 1 m
De belles discussions en perspective : certains sont déjà sur les starting blocks ! 
Vivement les questions suivantes de l'automatisation de la laiterie ainsi que les résolutions désarmantes, en trois lignes, de piepalm, biondo et autres nicolas_75 !
Philoux
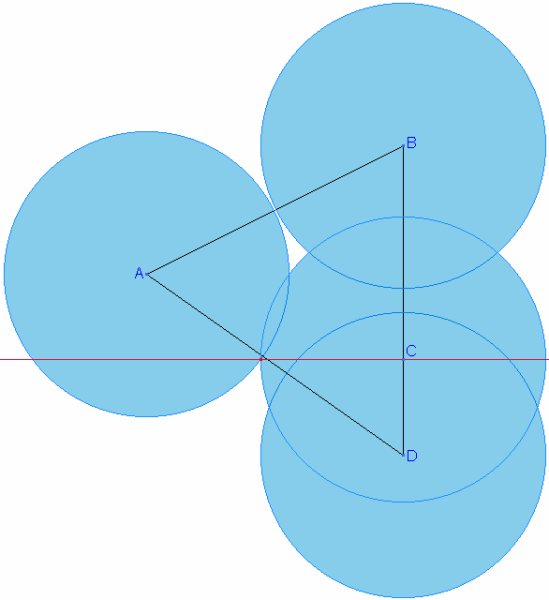
 Je ne suis pas sûr d'avoir compris la question, mais bon, va pour un éventuel poisson :
Je ne suis pas sûr d'avoir compris la question, mais bon, va pour un éventuel poisson :
Je suppose qu'il faut minimiser la somme des distances du bras aux 4 points, en tenant compte des caractéristiques du bras.
Il faut donc placer le bras à au moins 1m des 4 points (longueur mini du bras).
D'autre part, on doit conserver un angle de rotation max de 180°.
On place donc le bras à 1m de A et C (voir dessin), ce qui donne :
Distance à A : 1 m
Distance à B : √3,25 = env. 1,8 m
Distance à C : 1 m
Distance à D : √1,4489 = env. 1,2 m
D'autre part, on vérifie que l'angle AOD = env. 177° < 180°
Si on éloigne le bras du point O (vers le "sud"), la somme OA+OD augmente, ainsi que OB, et OC ne peut pas diminuer (on est déjà au mini), donc on est bien au plus près des points A, B, C, et D
 bonjour,
bonjour,
ma réponse sera le point 2 du dessin joint
explication.
j'ai placé les point A,B,C et D dans un repère.
on sait que le bras a une rotation maxi de 180° ainsi, il est a l'extérieur du triangle ABD.
ensuite, la longueur mini est de 1m. j'ai donc fait des cercles de 1m de diamètre autour de chaque point, coloriés en orange. Le bras est a l'extérieur des cercles oranges.
les deux points succeptibles de répondre aux attentes sont les point 1 et 2.
J'ai alors calculé les distances séparant les point 1 et 2 des points A,B,C et D.
la somme des distance 1A+1B+1C+1D est supérieur à la somme des distances 2A+2B+2C+2D.
le point 2 est donc le point le plus proche de A,B, C et D.
je vérifie tout de meme que ce point soit bien à l'extérieur du triangle et des cercles orangés.
Je calcul ses coordonnées.
il est sur la meme horizontale que C et sur le cercle orangé de A. j'appelle I le point sur la meme abscisse que 2 tel que AI perpendiculaire à BC
A2²=AI²+I2²
=> 1²=0.6²+AI²
AI=0.8
dans le repère Oij, le point 2 a pour coordonnées (1.5;0.8)
je vérifie qu'il soit à l'extérieur du triangle ABD en calculant l'angle (AI,A2) et (AI,AD)
l'angle (AI,AD)< l'angle (AI,A2)
le point 2 est bien à l'extérieur du triangle.
bon, je sais que je n'ai pas été super clair, car l'enigme est postée depuis 1j1/2 et je ne l'ai vu que maintenant, donc j'ai speedé.
j'espère que c'est clair
ma réponse est le point de coordonnées (1.5;0.8) dans le repère Oij
merci
Merci à tous de votre participation. Un grand bravo aux 4 personnes qui ont répondu correctement. Nofutur2, je t'ai tout de même adressé un smiley car bien que tu ai utilisé un logiciel tu as tout à fait bon dans la logique et sur d'autres énigmes, les réponses trouvées sont parfois sorties d'autres logiciels donc je t'ai attribué un smiley que tu le veuilles ou non  .
.
Malheureusement philoux, je crains que tu es oublié de tenir compte de la rotation maximum du bras robotisé, tout comme neozaki et goupi1.
Pour paulo c'est différent, tu as pensé au triangle mais tu n'as pas pris le soin de vérifier autre part que le côté AB 
Piepalm, tu étais dans la bonne logique malheureusement les distances données comme réponse ne sont pas correctes  ...
...
Pour sofyanekasunet, tu as oublié de faire attention à la rétraction maximum du bras, car si on place le point au milieu du segment AD, il est situé à moins de 1 mètre de A et de D.
Voila, en espérant que cette énigme aura été intéressante, voici une correction détaillée de la manière dont je m'y suis pris pour arriver à résoudre le problème (bien que ce fut plus difficile à élaborer par rapport aux mesures  )
)
Pour répondre à ce problème, il fallait commencer par tracer le triangle ABD dans le lequel le point P (bras robotisé) ne peut être situé du fait que le bras a une rotation maximum de 180°.
Ensuite il fallait tracer les cercles de rayon 1 à partir des centres A, B, C, et D. On pouvait ainsi remarquer les cercles Ca et Cc étaient sécants en un point extérieur au triangle. Et que visuellement sur un dessin, il se passe quelque chose d'intéressant entre les cercles Cb et Ca, il faut donc s'intéresser à ces deux régions de manière calculatoire.
Commencons par calculer la distance AB, En passant AB, dans un repère orthonormé de centre A, on a : xA = 0, yA = 0, xB = 1,8, yB = LA - EB = 5,1-4,2 = 0,9
On fait le calcul, et on trouve
Donc les cercles Ca et Cb, ne sont pas sécants, donc le point de cette région le plus proche de A, B, C et D est le milieu de [AB].
Passons dans un repère mettant en jeu tous les points nécessaires : A, B, C, D.
xA = 0
yA = 1,27
xB = 1,8
yB = 2,17
xC = 1,8
yC = 0,67
xD = 1,8
yD = 0
Calculons maintenant le milieu I de [AB] :
xI = (0+1,8)/2 = 0,9
yI = (1,27+2,17)/2 = 1,72
Le point le plus éloigné à I, est bien entendu le point D, calculons donc la distance [ID].
On fait le calcul et on trouve .
Laissons désormais cette région de côté pour s'y réintéresser plus tard.
A présent, intéressons nous aux cercle Ca et Cc, ils sont tout deux sécants en un point extérieur au triangle ADB. Calculons donc les équations de ces cercles.
Le cercle de centre A a pour équation :
Le cercle de centre C a pour équation :
On soustrait membre à membre pour obtenir :
On obtient :
On remplace dans l'équation du cercle de centre A, et obtient l'équation :
Je reconnais que pour être précis jusqu'au bout, cela oblige à manier des décimaux conséquent, mais jusque là on est parfaitement précis, on a encore rien n'arrondis...
delta = 74,6496
et chose intéressante, la racine de delta tombe juste !! comme quoi ce n'est pas si mal trouvé 
racine de delta = 8,64
on obtient les solutions :
y1 = 1,27
y2 = 0,67
On prend la solution la plus petite puisque le point d'intersection recherché est le plus bas, et on remplace dans la première équation de cercle
On obtient donc x1 = 0,8 et x2 = -0,8, on prend bien entendu x1 = 0,8 par rapport au dessin
Donc le point d'intersection des cercles Ca et Cc à l'extérieur du triangle ABD est le point J :
xJ = 0,8
yJ = 0,67
Calculons la distance JB qui est la plus grande, on trouve :
Donc JB < ID
Faisons un bilan des distances connues par rapport à I :
De même par rapport à J :
Il nous faut donc encore comparer les distances JD et IC,
Faisons maintenant la somme des distances par rapport à I et J :
Donc le point recherché est le point d'intersection entre le cercle de centre A et de rayon 1, et le cercle de centre C et de rayon 1, situé à l'extérieur du triangle ABD, tel que :


 >puisea
>puisea
j'ai posté cet après-midi (12:02 et 12:04) une analyse complémentaire qui montre que AR=1m est une solution éronnée.
Ta solution n'est pas optimisée : pour t'en convaincre calcules D²=JA²+JB²+JC²+JD² pour J valant le point R que je fournis R( x=1,017m ; y=1,292 m )
d'où les distances demandées, par Pythagore :
AR = 1,01725 m - BR= 1,17639 m - CR = 1 m (juste) DR=1,51077 m (valeurs approchées)
tu verras que ces distances fournissent une distance résultante plus faible (5,7010) que la tienne.
Sauf erreur...
(Je quitte l'île)
Philoux
(tu aurais pu/du laisser cette énigme plus longtemps pour permettre à d'autres mathîliens de participer : il y aura de la déception dans l'air pour certains...)
Philoux à moins de ne pas du tout te comprendre, ton point R est dans le triangle ABD, ce qui ne peut fonctionner du fait de l'hypothèse selon laquelle le bras ne peut pas tourner plus de 180°


Je n'ai pas participé à cette enigme car j'ai trouvé que l'énoncé n'était pas assez précis,
particulierement que signifie exactement "au plus près des 4 points" ?
de plus au vu des solutions proposées je pense que cette enigme aurez mérité plus de 2 étoiles.
Enfin si je dis ça c'est peut-être parce-que je suis faché de n'avoir pas su répondre ! 
En effet après avoir posté cette énigme, je me suis rendu compte qu'elle méritait sûrement plus d'étoiles à la vue des nombreux calculs qui fallait faire, si on voulait se passer d'un logiciel.
 Je n'avais simplement pas compris l'hypothèse de la rotation maximum du bras... j'ai pensé que c'était dans les transferts; dommage, le problème était un peu plus corsé...
Je n'avais simplement pas compris l'hypothèse de la rotation maximum du bras... j'ai pensé que c'était dans les transferts; dommage, le problème était un peu plus corsé...
Je crois que philoux a fait la même erreur, mais ma solution est meilleure (distance totale 4,64m contre 4,70m)!
 Je voudrais pas dire, mais Nofutur2 a demandé à ne pas être noté, pour éviter de prendre un poisson au cas où il aurait mal répondu.
Je voudrais pas dire, mais Nofutur2 a demandé à ne pas être noté, pour éviter de prendre un poisson au cas où il aurait mal répondu.
Je ne veux pas polémiquer, mais si on peut avoir des smileys dans ces conditions, j'utiliserai dorénavant sa petite phrase d'introduction pour toute mes réponses, comme ça, smiley ou rien !
Merci de ne pas prendre ma remarque trop au sérieux, je sais bien que ce n'est qu'un jeu, mais bon, vu que j'avais assumé le risque de prendre un poisson, j'ai du mal à comprendre ...
Merci à toi puisea pour toutes ces énigmes (et surtout celle-là que j'ai personnellement trouvé assez corsée, jusqu'à ce que je trouve cette réponse, pas si compliquée que ça finalement) et continue à nous triturer les méninges.
Tant que j'y suis, merci à tous les énigmeurs pour le temps qu'ils prennent pour nous...
Tout à fait d'accord avec toi jugo.
Il n'est pas juste que je récolte un smiley même si ma réponse est bonne, dès l'instant où j'ai souhaité jouer "à blanc".
Comme tu le dis, ce ne serait pas équitable par rapport à ceux, qui, comme toi, ont pris un risque que je n'ai pas voulu prendre..
Et puis çà créerait un précédent dont certains pourraient profiter à l'avenir.
Alors puiséa, merci pour ta décision, mais je ne peux l'accepter pour moi-même mais aussi vis à vis des autres concurrents.
Vous êtes trop forts... honnêtement, je n'ai rien compris à cette énigme. Un truc de mecs, je pense. Quand j'ai vu les chiffres un peu partout, j'ai à peine essayé 
 Merci Nofutur2 pour ton fairplay.
Merci Nofutur2 pour ton fairplay.
Il te reste quelques énigmes pour faire l'erreur qui tue.
Ensuite, je n'aurai plus qu'à convaincre levrainico de faire de même, et si j'évite les pièges, j'ai encore une chance.
Je compte sur vous pour ne pas me décevoir.
( comme quoi moi aussi je sais être fairplay 
 )
)


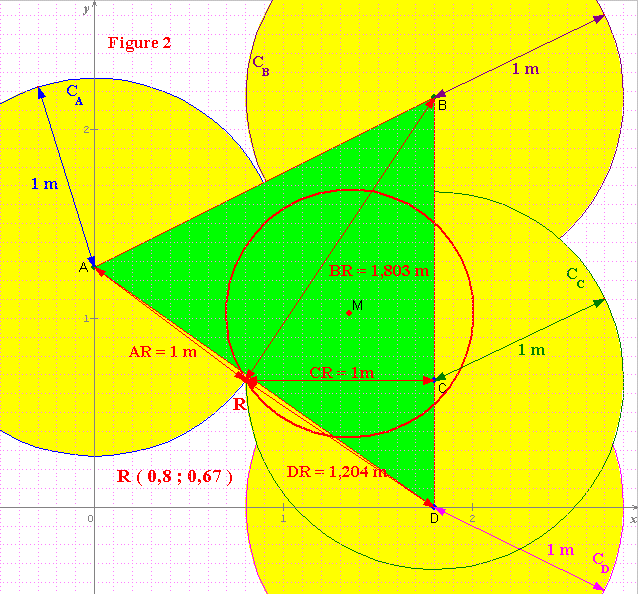
 Bonjour,
Bonjour,
Tout comme piepalm, j'ai considéré la contrainte de l'ouverture angulaire lors du transfert de bouteille : pour cette question, les 180° n'intervenaient donc pas...
En prenant en compte cette contrainte, le pb se résolvait tout aussi simplement :
1) positionner les 4 points A, B, C et D
2) tracer les cercles (jaunes) de rayon 1m pour tenir compte du bras mini=1m
3) tracer le triangle (vert) A B D pour tenir compte des 180°
4) déterminer M (1,35 ; 1,0275) qui est le point optimal sans contrainte; la famille de points optimaux est alors une famille de cercles concentriques en M : (x-1,35)² + (y-1,0275)² = D²/4 - 1,24441875
5) tracer le plus petit cercle (rouge) qui fournit un point en dehors des cercles jaunes et triangle vert.
Ce cercle a pour rayon MR=0,656 et fournit le point R(0,8 ; 0,67) qui est à l'intersection des cercles de centres A et C, de rayons unitaires.
AR=CR=1m ; BR=racine(13)/2 et DR=racine(14489)/10
Très belle énigme, dommage que l'énoncé souffre d'approximations; je suppose qu'il y a une suite (pour les autres chaînes d'embouillage)
Philoux
PS : bravo à Nofutur2 pour son fair play
Salut,
C'est vrai que lorsqu'on voit les réponses qui ont été proposé, on saisi mieux les éventuelles ambiguités que lorsqu'on met au point l'énigme...
Et ta supposition, philoux, est juste, je pense en effet faire une suite sur ce problème mais totalement différent, enfin j'y réfléchis encore. Pour l'instant il a quelques énigmes prêtes à sortir pour jusqu'à la fin du mois.
@+

Bonjour,
Je regardais le pdf des énigmes d'Octobre 2005 et le challenge 119 n'est pas complet il y avait probablement une image jointe.
Apparemment, cette image n'était pas sur le serveur du site... est-il possible de la retrouver ?
Merci.
Estelle 
Bonjour Estelle, effectivement, elle n'était pas sur le serveur de l'île... Personnellement, il semblerait que je ne l'ai plus en ma possession.
Nombre de participations : 0
Temps de réponse moyen : 20:26:25.