Inscription / Connexion Nouveau Sujet
Challenge n°128

Bonsoir, nouvelle énigme, alors bonne chance à tous :
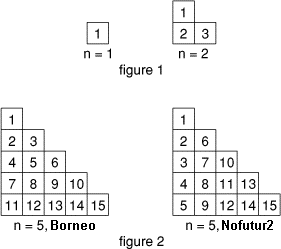
Pour tout entier strictement positif, on considère un tableau triangulaire, aligné à gauche, dont les n lignes ont de haut en bas, de 1 à n cases. On peut y inscrire les entiers dans l'ordre naturel : 1, 2, 3, ..., à raison d'un seul par case.
Borneo remplit ses tableaux ligne après ligne en partant du haut, tandis que Nofutur2 les remplit colonne après colonne en partant de la gauche.
Pour n = 1 et pour n = 2, les tableaux remplis par Nofutur et Borneo sont identiques; ils ont respectivement 1 et 3 nombres inscrits dans la même case (figure 1).
Pour n = 5, les tableaux sont différents, mais ils ont 5 nombres inscrits dans la même case: 1, 2, 8, 14, et 15 (figure 2).
Quelle est la plus petite valeur de n après 5 pour laquelle les tableaux ont aussi un nombre impair de nombres inscrits dans la même case ?
 Comme 1 et 2 sont toujours a la même place alors il faut soit multiplier 5 par 1 ou alors par 2 pour avoir le meme cas ou il y a un chiffre impair de nombre à la même place.
Comme 1 et 2 sont toujours a la même place alors il faut soit multiplier 5 par 1 ou alors par 2 pour avoir le meme cas ou il y a un chiffre impair de nombre à la même place.
=====> N=10 

 Si on utilise la notation matricielle pour une matrice triangulaire de côté n, on trouve que la les coefficients de la matrice de Bornéo b(i,j) (avec j<=i<=n) sont tels que :
Si on utilise la notation matricielle pour une matrice triangulaire de côté n, on trouve que la les coefficients de la matrice de Bornéo b(i,j) (avec j<=i<=n) sont tels que :
b(i,j) = i(i-1)/2 + j
Avec les mêmes notations pour la matrice de Nofutur (quel honneur !!): n(i,j) = i + (j-1)n-j(j-1)/2.
Il suffit de trouver les solutions b(i,j) = n(i,j) en faisant varier n à partir de 6 et de compter le nombre de solutions.
Il faut aller jusqu' à une matrice triangulaire de côté n =22, pour trouver un nombre impair de solutions, à savoir :
b(1,1)=n(1,1) = 1
b(2,1)=n(2,1) = 2
b(16,7)=n(16,7) = 127
b(22,21)=n(22,21) = 252
b(22,22)=n(22,22) = 253
Soit 5 solutions.
Le plus petit nombre n >5, tel que le nombre de solutions est impair est donc n=22.
Pour information le suivant est n=121 avec 7 solutions.


 Sans conviction Je trouve n=22
Sans conviction Je trouve n=22
et dans ce cas les deux tableaux ont 5 nombres inscrits dans la même case


 on trouvera n=6
on trouvera n=6
dans ce cas on va trouver les nombres 1 ; 2 ; 21
 La plus petite valeur est n=22; la suivante est 161
La plus petite valeur est n=22; la suivante est 161
En effet, les valeurs de la case de la ligne p colonne q coïncident dans les deux tableaux si
p(p-3)+q(q-1)=2n(q-1)
Ces valeurs vont aller par paire (au couple p,q étant associé le couple n+1-q, n+1-p: il est facile de voir que si l'un est solution l'autre aussi) sauf si p+q=n+1 auquel cas l'équation devient q²-(2n-1)q+(n²+n-2)/2=0 qui aura une solution positive entière si le discriminant 2n²-6n+5 est un carré ce qui est vrai pour n=5, 22, 161,...
 J'ai pris la méthode bourin jusqu'à 14, et puis je me suis dit que ça pouvait durer longtemps. J'ai vu que le tableau était symétrique et que ça devait se passer sur la diagonale. Donc je n'ai pris que les nombres sur la diagonale, et j'ai construit un tableau que j'aurais pu prolonger à l'infini...
J'ai pris la méthode bourin jusqu'à 14, et puis je me suis dit que ça pouvait durer longtemps. J'ai vu que le tableau était symétrique et que ça devait se passer sur la diagonale. Donc je n'ai pris que les nombres sur la diagonale, et j'ai construit un tableau que j'aurais pu prolonger à l'infini...
Ma réponse est 22.
Merci pour l'énigme.
 Bonjour,
Bonjour,
La plus petite valeur de n après 5 pour laquelle les tableaux ont aussi un nombre impair de nombres inscrits dans la même case est


 bonjour,
bonjour,
Je trouve n=22
Au fait, merci Excel et Visual Basic...
 Bonsoir,
Bonsoir,
En notant (i,j) la valeur de la case à la i-ème ligne et j-ième colonne (avec ji), on a:
Pour borneo, (i,j)=
Pour Nofutur2, (i,j)=
Reste à étudier le nombre de cas d'égalité en fonction de n.
Là, je suis passé par un petit programme...
La prochaine valeur de n est , il y a 5 cases identiques dans les deux tableaux (1,2,127,252 et 253).
La valeur suivante de n est , avec 7 cases égales (1,2,1091,3691,6291,7380 et 7381).
Conclusion: est la prochaine valeur de n cherchée.
Il doit bien avoir une façon d'éviter la programmation (raisonnement matriciel avec utilisation de la "symétrie" par exemple) mais je n'ai pas trouvé...
Merci pour l'énigme.
 j'en sais rien alors je vais dire qu'il n'y en a pas parceque la jsuis arrivé a plein d'otération et j'ai pas envie de le programmer
j'en sais rien alors je vais dire qu'il n'y en a pas parceque la jsuis arrivé a plein d'otération et j'ai pas envie de le programmer
donc j'espère que c la bonne réponse 
 oh bah non je me suis trompé !
oh bah non je me suis trompé !
j'étais a peine heureux d'avoir eu bon a l'enigme de J_P !

-1 au classement c'est pas très glorieux... 
Seb
 Vu le temps que j'ai mis à trouver la méthode "intelligente", j'aurais mis moins de temps avec la méthode "bourin" (que j'ai tout de même pratiquée jusqu'à n=15)
Vu le temps que j'ai mis à trouver la méthode "intelligente", j'aurais mis moins de temps avec la méthode "bourin" (que j'ai tout de même pratiquée jusqu'à n=15)
Voilà le tableau où sont toutes les valeurs correspondant auw différences entre les deux tableaux, en ne retenant que les cellukes de la diagonale.
Super énigme pour amateur de tableur...
 Bonjour
Bonjour
L'utilisation d'un tableur était semble-t-il la voie la plus appropriée et la plus employée. Ce n'est pas celle que j'ai pratiquée.
Grâce à la symétrie on remarque assez vite qu'il suffit de s'intéresser uniquement à la diagonale.
Après avoir égalé les 2 "équations" de la diagonale j'arrive à :
(3+4xn+
Rq : les indices n n'ont rien à voir avec le n du problème.
Il faut qu'on ait un carré parfait sous la radical. On résout cette équation Pell-Fermat et on trouve :
x0 = 1
xn = yn-1+ 3xn-1
avec y0 = 3 et yn = 3yn-1 + 8xn-1
On obtient les différents n qui sont sauf erreur : 5, 22, 121, 698,...
 Je pense moi aussi que cette énigme se résolvait sans tableur. Encore faut-il ne pas faire d'erreur de calcul (ou de copie...: je ne sais pas comment j'étais arrivé à 161 (au lieu de 121 pour la valeur suivante).
Je pense moi aussi que cette énigme se résolvait sans tableur. Encore faut-il ne pas faire d'erreur de calcul (ou de copie...: je ne sais pas comment j'étais arrivé à 161 (au lieu de 121 pour la valeur suivante).
Pour les inconditionnels des tableurs, il faudra que je retrouve un petit problème qui les met en défaut...
Nombre de participations : 0
Temps de réponse moyen : 22:36:09.


