J'arrive à une formule assez compliquée que je vais décomposer en deux .
A= (999+997)*(2*25³/3)
B=2*(x-25)*(-25²+(x-25)²/3)

Le résultat en secondes (x étant en cm) est :
t=[/(999*997)]*(A+B)

Pour x=2R, c'est à dire pour un trou "latéral" placé en haut, on obtient :
t=*(1/999)*(4*R³/3).
On confirme bien que dans ce cas le temps de remplissage est égal au volume de la sphère sur le différentiel de vitesse entre l'entrée (1000cm³) et la fuite du bas(1cm³).

Bonjour
Temps (en s) = (2pi/3x997x999)(2x25³x999-75x²+x³)

Je donne mon résultat, je justifierai ensuite.
secondes (avec x sans dimension : la valeur de la longueur en cm).

Bonjour
Le temps total:
T= п/2991[62500+2x^2(x-75)/999]
Merci pour l'lenigme.

Si je n'ai pas fait d'erreur en tapant sur ma calculette je trouve que le temps (en secondes) peux 'éxprmier en fonction de x (en cm) par l'expression suivante:

Bonjour,

Je trouve la formule suivante pour le temps de remplissage de la sphère en fonction de x. Le temps t est en secondes, et x doit être donné en cm :



Merci pour l'énigme !

Alors l'expression du temps en fonction de x se décompose en 2 expressions
La première si la hauteur du 2 eme trou est supérieure au rayon de la sphère
La deuxième si la hauteur du deuxième trou est inférieure au rayon de la sphère

Cas 1: x>25cm



Cas 2: x<25cm



En espérant ne pas m'étre tromper, je pense que faire ca au saut du lit n'est pas forcément la meilleure idée que j'ai eu
Mais de toute façon merci pour l'énigme je l'ai trouvé très intéressante à résoudre.

Bonjour!
Tout d'abord je tenais à remercier puisea pour cette très belle énigme, car j'ai vraiment pris plaisir à la chercher...
j'ai passé pas mal de temps à cogiter, et au final, je trouve :

t(x)= (62500 )/2991 - (2500 x)/2988009

J'essayerai de poster mon raisonnement plus tard si j'en trouve le temps!!
++
Marie.

Bonjour,

A condition que x soit bien la hauteur du plan horizontal où est positionné le trou T3, par rapport à la base de la sphère, où est positionné le trou T2, l'expression du temps de remplissage de la sphère en fonction de x est la suivante (voir image attachée)
Rq1 : t est exprimé en secondes et x en centimètres

Rq2 : On doit avoir besoin de connaître t avec une grande précision, non ??
      Le volume de la sphère est 65,45 litres
      Le débit d'alimentation par le trou T1 est de 1 litre par seconde
      Les débits de fuites sont de 10^-3 litre par seconde en T2 et 2.10^-3 litre par seconde en T3...

S'il n'y a pas de trous, t65,45 secondes
Si T2 et T3 sont confondus en un seul trou, et que l'on admet que la fuite de ce trou soit de 10^-3 + 2.10^-3 = 3.10^-3 litre par seconde, t65,65 secondes
Si T1 et T3 sont confondus en un seul trou, et que l'on admet qu'il y ait un refoulement de 2.10^-3 litre par seconde sur le litre par seconde entrant, t65,52 secondes

Soit une variation de t de 0,197 seconde maxi !!!

A bientôt, KiKo21.

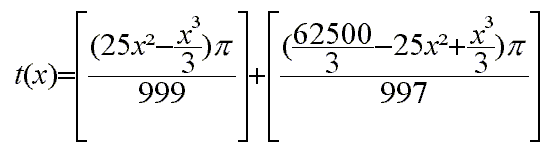
Je ne suis absolument pas sur de ce que je trouve mais bon qui ne tente rien n'a rien alors je me lance :

Je trouve (si l'on prend x en cm) que le temps pour remplir la sphère est de

T=(2x³-50000x²+499925³)/(9999973) secondes

soit T=(2x³-50000x²+62437500)/(2988009) secondes

Pour que la sphère soit intégralement remplie, il faut en secondes t=65449*[(100-x)/99900+x/99700].

Quelle nouille je fait je viens de me rendre compte que le x de ma réponse n'est pas le même que le x de l'énoncé.
En fait il faut remplacer le x de ma réponse par x-25.

Donc par ici le

Dommage de finir le mois sur une erreur aussi bête, j'essaierai de me ratrapper le mois prochain ..

Bonjour.

Je considère la sphére comme 2 calottes sphériques.
La première, de hauteur x se remplie à 999 cm3/s.
La seconde, de hauteur 50-x se remplie à 997 cm3/s.
Volume d'une calotte : V = (pi/3)h²(3r-h) avec h, hauteur de la calotte et r, rayon de la sphère.
Ainsi, le temps cherché en fonction de x est :

(pix²(75-x)/2997)+(pi(50-x)²(25-x)/2991)

Ce qui donne :

(pi/2988009)(2x3 - 150x² + 62437500)

Merci pour les énigmes.
A+

Bonjour, allez, je me lance, même si je prends un poisson, ça ne me fera pas sortir du classement.
J'espère que j'ai bien compris l'énoncé...

Je me sers de la formule du volume d'une calotte en fonction de la hauteur et je considère un débit de 999 cc/s sous le trou de côté et 997 cc/c au dessus du trou.

Je calcule tout ça, je mets au même dénominateur, et j'obtiens une méga formule :

temps (en seconde) = (2x³ - 150 x² + 62437500)/2988009

je n'ai pas pu faire plus simple.

Merci pour l'énigme

temps necessaire pour remplir la sphere avec r = 50 cm, D2 = 1 cm3 / s, D1 = 1 dm3 / s, D3 = 2 cm3 / s et x etant la hauteur du trou :

T = /3*x²(3r-x)/(D1+D2) + /3*(4r³-x²(3r-x))/(D1+D2+D3)

Soit

T = /3 * (x₃*(2/996003) + x²*(100/332001) + 500000/997)



T ~ 1.05 * (2*10^-6-x²*3.01*10^-4 + 5.01*10²)
T ~ 500 s

salut,

en appelant



La sphère se remplit jusqu'a la hauteur x avec un débit valant d_T1-d_T2.
Le volume d'eau à ce moment (qu'on appelle t_x) vaut
d'où

La sphère se remplit ensuite avec un débit valant

La sphère sera remplie au temps

avec
r=25cm
d_T1=1000 cm³/s
d_T2=1 cm³/s
d_T3=2 cm³/s


t en seconde

Ptitjean

Bonjour, et merci encore pour cette énigme.

Ne connaisant pas la précision demandé du temps, je répondrais que quelque soit la valeur de x compris entre 0 et 50, le temps total ne variera que de 0.13 seconde a peine.

J'en concluerai donc qu'il faut un peu plus de 65.5 seconde pour que la sphère soie intégralement remplie soit 66 secondes et ce dans n'importe quelle valeur de x!

Merci et à bientôt!

Bonjour,

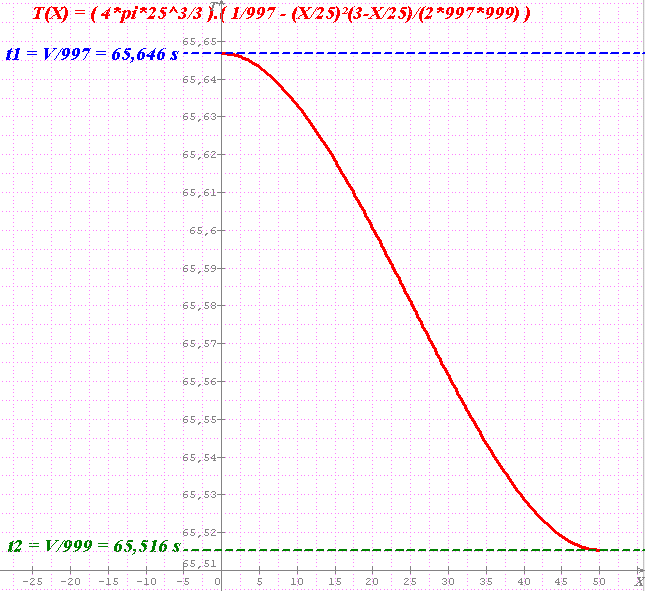
Réponse proposée :

T(X) = (4piR^3/3)( 1/997 - (X/R)²(3-X/R)/(2*997*999) ) avec 0 < X < 2R

Méthode proposée :

Tout d'abord, avec un peu de bon sens et sans utilisation d'intégrales, on peut dire que le temps de remplissage variera entre :

t1=V/999 et t2=V/997 avec V=volume de la sphère en cm3 et t1 et t2 en s
puisque la sphère se remplit au débit de :

* v1=(1000-1) cm3/s si le trou est tout en haut => X = 2R = 50cm

* v2=(1000-1-2) cm3/s si le trou est tout en bas => X = 0 cm

Le volume de la sphère valant 4piR^3/3 = 4pi(25)^3/3 # 65 450 cm3

le temps nécessaire, T, est donc compris entre :

65,516 s < T < 65,646 s soit environ 65,6 s


DOnnons, comme demandé, l'expression de T(X) avec 0 < X < 2R

A) Cas où X=2R (pas de fuite latérale)

On peut écrire l'égalité de variation de volume pendant dt, l'eau dans la sphère étant à la hauteur x, en partant du bas.

Pendant dt, il rentre Ve.dt, sort Vs.dt et le volume augmente de dv : Ve.dt = dv + Vs.dt

Si la hauteur est x, le volume dV est celui d'un cylindre de hauteur dx pour un rayon r(x) fourni par Pythagore :

r(x)² + (R-x)² = R² => r(x)² = 2Rx - x² => dv = (pi.r(x)²).dx = pi(2Rx-x²)dx

ainsi (Ve-Vs)dt = v1.dt = pi(2Rx-x²)dx => S(1000-1)dt = piS(2Rx-x²)dx

999t+K = pi.x²(Rx-x/3)

comme à t=0, x=0 => K=0 et t=(1/999)pi.x²(3R-x)/3
on retrouve bien le fait que si x=2R => t = t1 = (1/999)(4pir^3/3)

B) Cas où la fuite est située à X en partant du bas

Calculons le temps nécessaire, tX, pour remplir la sphère à la hauteur X :

tX = (1/999)pi.X²(3R-X)/3

il restera à remplir la hauteur (2R-X) au débit de v2=Ve-Vs-Ws avec Ws = 2 cm3/s;
ainsi, selon le même raisonnement, le temps t'X vaudra :

t'X = (1/997)pi(2R-X)²(3R-(2R-X))/3 = (1/997)pi(R+X)(2R-X)²/3

Il suffit enfin de dire que T=tX+t'X = (pi/3)[X²(3R-X)/999 + (R+X)(2R-X)²/997]

Désirant faire apparaître le volume V de la sphère ( 4piR^3/3), et en passant en coordonnées réduites u=X/R, on peut aussi écrire :

T = (4piR^3/3)( u²(3-u)/999 + (1+u)(2-u)/997 ) avec 0 < u < 2

T = (4piR^3/3)( 1/997 - u²(3-u)/(2*997*999) ) avec 0 < u < 2 soit enfin :

T = (4piR^3/3)( 1/997 - (X/R)²(3-X/R)/(2*997*999) ) avec 0 < X < 2R

Et donc la courbe ci-dessous.

Merci pour l'énigme,

Philoux

Nota : l'énigme de puisea ressemble grandement à celle de J-P avec son sceau troué...

Le volume d'eau en cm3 dans la sphère remplie jusqu'à la hauteur x en cm est:
pi*x^2(25-x/3)=78,54x^2-1,047x^3, celui de la sphère pleine est pi*62500/3=65450 cm3
Le débit de remplissage est d1=999 cm3/s jusqu'à la hauteur x et d2=997 cm3/s au delà.
Le temps nécessaire pour remplir la sphère sera donc:
t=pi*x^2(25-x/3)/d1+(pi*62500/3-pi*x^2(25-x/3))/d2
=pi*((1/d2-1/d1)(x^3/3-25x^2)+62500/3d2
=x^3/475556-x^2/6341+65,65 en secondes
Les variations sont infimes puisque t vaut 65,65s pour x=0, et 65,51s pour x=50cm

je pense que le temps nécéssaire au remplissage intégral de la sphère est (unités : cm, seconde) :

égal aussi à :


mais bon je n'en suis pas sûr du tout...

Bonjour,

t est exprimé en s (seconde) et x en cm.



Courage pour la correction.

Bonjour
Volume en cm³ de la calotte sphérique inférieure = pi.(75x² - x³)/3 ; débit rentrant pour elle = ( 1000 - 1 )cm³/s =  999 cm³/s
Volume en cm³ de la calotte sphérique supérieure = pi.(x³ - 75x² + 62500)/3 ; débit rentrant pour elle = (1000 - 1 -2 )cm³/s = 997 cm³/s
donc le temps en secondes pour remplir la sphère =
pi.(75x² - x³)/{3*999}  +  pi.(x³ - 75x² + 62500)/{3*997} =
  =
  =
  =
  =


geo3

Bonsoir,

je crois avoir fait une erreur de transcription.
999.62500 = 31218750  et non 3128750 comme je dois l'avoir écrit!
Il manque le chiffre 1 après 312 !

allé je me lance, mais quand meme les 4 etoiles me font douter

il faut : x²(75-x)/2997 + 62500/2991 -x²(75-x)/2991 secondes

Ceci dit, ce qui fait encore plus bizarre c'est que le trou soit tout en haut ou tout en bas çà fait quasiment le meme temps : entre 65.50 et 65.7 secondes

Bonjour et merci d'avance pour cette dernière énigme marsienne.

Après quelques réticences dues au fait que l'énoncé avait un dernier goût de physique je me suis dit que j'allais cherhcer un peu parce que les hypothèses de la première phrase semblaient indiquer que le problème allait avoir une solution uniquement "mathématique". (pas de frottement etc...)

Donc si j'ai bien compris, pour moi, le problème se ramène à déterminer le temps mis pour remplir le volume de la calotte avec un débit de 999 cm^3/s pour une calotte de hauteur x et avec un débit de 997 cm^3/s pour la partie restante.

Je doute que ce soit ça car il y a 4 étoiles et il y a sûrement des problèmes physiques à prendre en compte.

Si mon hypothèse est bonne alors voici ma réponse détaillée.

Première remarque :

Le volume de la sphère de rayon 25 cm est 4*pi*25^3/3 soit environ 65,4498946... dm^3 donc sans trou de fuite le temps de remplissage serait d'environ 65,5 secondes.

Je pars du principe que le trou du bas entraine que la sphère se remplit avec un débit de 999 cm^3/s jusqu'à ce que l'eau atteigne le deuxième trou et qu'ensuite elle se remplit avec un débit de 997 cm^3/s.
Si cette hypothèse est une simplification extrème du problème alors ma réponse est sûrement fausse. Tant pis...

Sachant que le volume d'une calotte sphérique de rayon R et de hauteur x est donné par la formule :

V = pi*h^2(R-h/3) = (pi/3)(3Rx^2-x^3), je trouve les résultats suivants.

Temps de remplissage de la calotte inférieure de hauteur x : (pi/3)(3Rx^2-x^3)/999 en secondes

Le volume restant est (pi/3)(4R^3-3Rx^2+x^3) donc le temps de remplissage de la calotte supérieure est :

(pi/3)(4R^3-3Rx^2+x^3)/997

Le temps total en fonction de x et de R est donc (pi/3)(3Rx^2-x^3)/999 + (pi/3)(4R^3-3Rx^2+x^3)/997

Avec R=25 cela donne en fonction de x uniquement :

(pi/3)(75x^2-x^3)/999 + (pi/3)(62500-75x^2+x^3)/997

En mettant au même dénominateur et en transformant voilà la forme la plus belle que j'ai pu trouver pour cette valeur.

(2pi/3*999*997)*(x^3 - 75x^2 + 999*62500/2)

ou encore (2pi/2988009)*(x^3 - 75x^2 + 31218750)

J'essaie une écriture plus jolie avec le symbole pi : (2/2988009)*(x³-75x² + 31218750)

Cette dernière valeur (en secondes) est donc ma réponse à cette énigme.

J'ai un peu testé ce résultat et sur l'intervalle [0;50], la valeur maximale est atteinte pour x = 0 qui correspond en fait à un trou en bas de débit 3 cm^3/s. Cependant cette valeur est seulement légèrement supérieure à la valeur obtenue en l'absence de fuite.

Je trouve en effet 65,646787311722526714782752074547 secondes à comparer aux 65,449846949787359134638403818323 en l'absence de fuite.

Soit un écart de 2 dixièmes de seconde !

Sans conviction, et sauf erreur de calcul.

minkus

Le temps de remplissage de la sphère est de :

T=(2x³-150x²+62437500)*/2988009

Avec T en secondes et x en cm

Comme son expression est un peu longue à écrire, j'ai mis la formule du temps de remplissage dans le fichier attaché.
Merci

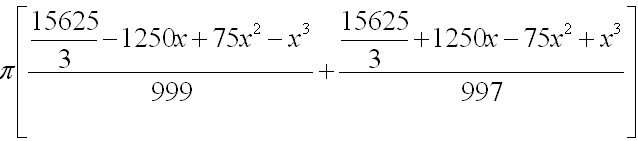
Bonjour,

Tant que l'eau est en-desous du trou "latéral", la sphère se remplit à raison de 999 cm3/s. Dès que l'eau arrive à cette hauteur x, la sphère se rempplit à raison de 997 cm3/s.

Ce qui nous donne un temps de remplissage de:
  T = (pi/3)*x²*(75-x)/999 + (pi/3)*(50-x)²*(25+x)/997 secondes

Je ne développe pas plus, sans Latex, c'est abominable...

Quoi qu'il en soit T varie entre 58.7335 s pour x = 6.125 cm et 70.9734 s pour x = 27.75 cm.

A+,
gloubi

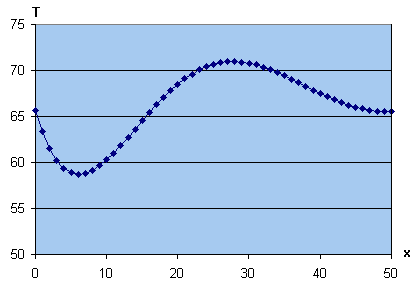
Voilà ma réponse : t= (-(3x-100))/(996003(x-25)²)- (4x³)/2988009
+200x²/996003 - (6250001x)/622501875 + 133984379/24900075

Méthode utilisée: Tout dabord on calcule le volume de la colotte sphérique au niveau de T3. Une fois ceci fait, on soustrait ce qu'on a obtenu au volume total. Ainsi on obtient le volume d'eau qui sera éventuellement remplie et dont la vitesse de remplissage dépend  de T1 et T2, la vitesse d'écoulement est vT1-vT2 évidement.Ensuite arrive le remplissage de la colotte sphérique supérieure, au niveau de T3.La vitesse de remplissage est (vT1-vT2)-vT3 (evidement puisque T2 n'est pas bouché).

Bonjour, je trouve un temps t en seconde qui est:
t = [+]

temps=volume (m^3) /debit (m^3/s)

t=((/3)*(x)^2*(3*0.25-x))/(0.001-0.000001)  + ((/3)*(0.5-x)^2*(3*0.25-0.5-x))/(0.001-0.000001-0.000002)

c'est la somme de la sphere séparée en 2 calottes sphérique.
Le volume d'une calotte sphérique est (/3)× h² × (3r-h) où r est le rayon de la sphère et h la hauteur de la calotte.

oh yeah esperons que c'est bien ca... Merci de m'avoir fait me pencher sur le volume d'une portion de sphere

rebonjour, et oui je sais seule la première réponse compte... Mais histoire de développer ma réponse, je voulais ajouter que mon équation du temps est:


               2x³        50x²       *62500
    T=     -------   -   -------  +  ------
           2988009       996003       2991

Voilà! histoire de montrer que je me suis un peu casser la tête quand même! lol

A bientot pour le moi d'avril sans poisson! (d'avril)

Bonjour je vais essayer de proposer une réponse mais je ne suis vraiment pas sur.

Je suis partis sur le principe que le volume de la section etait proportionnel à x, j'ai arrondi le resultat:

t=156.13-0.03x

erff excuser moi une faute très bête, erreur de signe que j'ai vu dans mon brouillon, sinon la réponse est bien:
t= (-2(2x³-225x²+9375x-31312500))/2988009

salut
soit T1 la duree de remplissage de la premiere partie de la sphere
V1 le volume de cette partie
et D1 le debit durant cette periode
on a V=DT
quel est V1
quel est D1
calcul de T1
meme travail pour la deuxieme partie
calcul de V1
par une integrale on trouve V1=2R³/3 + x(R² - x²/3)
D1=(1dm³-1cm³)/s=999cm³/s
t1=V1/D1

pour V2=Volume de la sphere - V1
4/3R³-V1=2R³/3 - x(R²-x²/3)
et D2=997cm³/s
t2=V2/D2


TEMPS TOTAL=t1+t2

Bonjour tout le monde !

Pour ma toute première participation aux énigmes j'espère ne pas commencer avec un poisson, mais bon faut pas rêver ...

Bref, après de longs calculs (mais en math tout le monde sait que plus c'est long, plus c'est bon ...), j'ai trouvé que :
t = (pi/2 988 009) * (2x^3 -150x² + 62 437 500)

Merci pou l'énigme et à la prochaine !

Cette énigme ressemble beaucoup à un "simple" exercice de volume ...

Je calcule dans un repère orthogonal centré sur O, centre de la boule.
Je considère r [-25; 25]
Je note h l'ordonnée du point latéral, h [-25; 25]
Je note A(r) l'aire d'un disque (section horizontale de la boule)

Commençons par calculer le volume d'eau en dessous du trou latéral :











Voyons maintenant le remplissage de la boule
Au départ l'eau entre par le dessus et ne sort que par le trou du bas :

    
NB : je mets toutes les valeurs en cm ou équivalent (
pour un volume)





Au moment où l'eau atteint le trou latéral, on a le volume .


On obtient

On continue le remplissage, cette fois l'eau sort par les deux trous :







Au temps , la boule est totalement remplie donc



d'où

Le temps mis pour remplir la boule est



J'ai trouvé le temps en fonction de h mais il me le faut en fonction de x
J'ai posé h [-25; 25] alors que x [0; 50], je pose donc x = h + 25

J'obtiens :


en plaçant x entre 0 et 50 cm on obtient un remplissage entre 1'05,52'' et 1'06,47''

Soit t, le temps (en secondes) necessaire au remplissage de la sphere:

Merci à tous de votre participation à cette énigme.

Yessss ! Je crois que les 4 étoiles ont effrayé des mathîliens qui auraient pu trouver...

Dur, le corrigé des petits malins qui n'ont pas effectué

Merci pour l'énigme et bon week end

Et un grand bravo à jacques1313

Bonjour puisea,

En ce jour du premier avril, merci pour le !

Bravo à ceux qui ont trouvé, et en particulier à jacques1313 pour sa victoire au classement de mars.
Bonne chance à tous pour le mois qui débute !

J'fais des trous, des p'tits trous encore des p'tits trous...
Merci à tous, ça me fait bien plaisir d'avoir gagné mais ça s'est joué à presque rien.

Bonjour,

Jolie énigme pour clôturer le mois.
Cela ressemblait en plus difficile à mon tonneau de jardin avec ses fuites et les averses de mars.

Bravo à jacques1313, très méritant sans aucun conteste.

Borneo, tu m'as un peu déçu en ne donnant pas ta réponse sous Latex...
C'était une bonne occasion pour s'exercer, avec une méga-formule !!
(T'as vu, je progresse... )

Bon courage à tous pour avril, le mois des poissons comme tu l'as fait remarquer vince909 !

A+, KiKo21.

Salut Kiko21, ma formule étant développée et réduite (comme on dit dans les topics du collège...) elle n'avait pas vraiment besoin de latex. On ne peut pas en dire autant de la tienne

Je te félicite néanmoins pour ton latex, très esthétique

Bon week end

Bonjour Puisea
Pourrais-je savoir pourquoi, en ayant la même formule que Jacques1313 et Geo3 (je n'ai pas comparé aux autres formules qui sont présentées différemment) il ont juste et moi faux ?

En tous cas bravo à puisea pour la correction de cette énigme, car ça devait être assez pénible de vérifier toutes ces expressions sous des formes très différentes.

Quel courage !