Inscription / Connexion Nouveau Sujet
Challenge n°193 : arcs
Bonjour à tous, nouvelle énigme qui m'a été suggéré par infophile (merci à lui) :
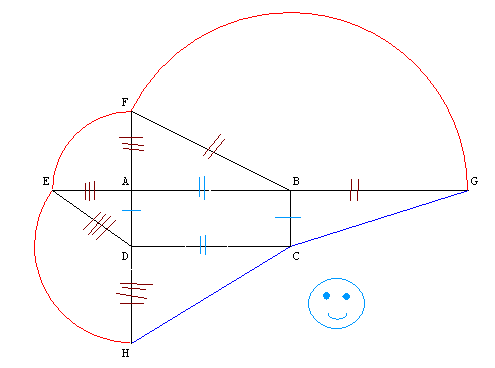
Démontrez que HC = CG.
ABCD est un rectangle.
Les arc de cercle en rouge ont pour centres les points du triangle ABD.
Bonne chance à tous.
 Bonjour,
Bonjour,
HC²=CD²+DH² (pythagore)
HC²=CD²+ED²
HC²=CD²+AD²+EA² (pythagore)
HC²=CD²+AD²+FA²
HC²=AD²+AB²+FA²
HC²=AD²+BF² (pythagore)
HC²=BC²+BG²
HC²=CG² (pythagore)
Donc, HC=CG
Fractal 

 Bonjour
Bonjour
Je pense qu'il faut utiliser plusieurs fois le theoreme de Pythagore (on a beaucoup de triangles rectangles  ).
).
On a dans le triangle BCG, CG²=BC²+BG²=AD²+BG².
Or dans le triangle ABF, on a:BF²=AE²+AB² (car AE=AF)
donc CG²=AD²+AE²+AB² car BG=BF.
De plus dans le triangle EAD, on a: AE²=HD²-AD²
et dans le triangle HDc, on a: HC²=HD²+AB² (car AB=DC)
donc HC²=HD²+AB²=AB²+AE²+AD² car AE²=HD²-AD²
d'où HC²=AB²+AE²+AD²
On en déduit donc que HC²=CG²
donc HG=CG car ce sont des longueurs 
Joelz
Merci pour la JFF 
 Bonjour!
Bonjour!
CG²= BG²+BC²
= BC²+BF²
= BC²+BA²+AF²
= BC²+BA²+EA²
= BC²+CD²+EA²
= DC²+AD²+EA²
= DC²+ED²
= HC²
Donc HC = CG car une distance est toujours positive 
Bon, pour la justification, ben c'est du Pythagore quasi à chaque étape...
J'ai supposé que EABG et FADH étaient alignés, j'espère que c'était bien ce qu'il fallait faire pasrceque à bien y réfléchir, ça me parait trop simple pour être vrai...
lolo 
 J'utilise essentiellement le théorème de Pythagore.
J'utilise essentiellement le théorème de Pythagore.
HC2=DC2+DH2 (Pythagore)
HC2=DC2+DE2 (car DE=DH)
HC2=DC2+AD2+AE2(Pythagore)
HC2=AB2+BC2+AF2 (car AB=DC, AD=BC et AE=AF).
HC2=AB2+BC2+(FB2-AB2).(Pythagore)
HC2=BC2+FB2
HC2=BC2+BG2 (car FB=BG)
HC2=GC2(Pythagore)
S'agissant de longueurs, donc de valeurs positives, j'en conclus que HC=CG
 Bonjour,
Bonjour,
On sait:
(- rayons dans le trois cercles)
et
AB=CD, AD=BC (cotés du rectangle)
On a:
DONC HC=CG
Merçi pour l'énigme.
 Bonjour,
Bonjour,
Comme dirait Minkus,
merci Pythagore,
merci Pythagore,
merci Pythagore,
merci Pythagore,
merci Pythagore.
 Salut,
Salut,
Tout d'abord, ABCD est un rectangle donc et
.
AF et AE sont deux rayons du même cercle de centre A donc .
On raisonne de même pour montrer que et
.
On applique ensuite le théorème de Pythagore dans le triangle ABF, on obtient .
En ajoutant dans chaque membre, on obtient :
.
Puis d'après le théorème de Pythagore dans ADE, on a .
En remplaçant par
dans
, on obtient
Or d'après le théorème de Pythagore dans les triangles CDH et BCG, on a et
.
D'où d'après la relation , on obtient
.
Donc finalement .
à+

 Bonjour,
Bonjour,
comme on a des arcs de cercles,
BG = BF
ED = DH
AE = AF
comme on a un rectangle,
AB = DC
AD = BC
Avec Pythagore, on a
CG² = BC² + BG²
CG² =AD² + BF²
et encore Pythagore :
CG² = AD² + AF² + AB²
Toujours Pythagore :
HC² = HD² + DC²
HC² = ED² + AB²
et encore Pythagore :
HC² = AD² + AE² + AB²
HC² = AD² + AF² + AB²
on voit donc que CG² = HC²
comme ce sont des segments (valeurs toujours positives) on peut dire que CG = HC
cqfd
Merci pour cette énigme. Infophile, on t'attend de pied ferme dans les énigmes de juillet.
 Bonsoir,
Bonsoir,
très joli exercice (je le met de côté  Merci Kévin).
Merci Kévin).
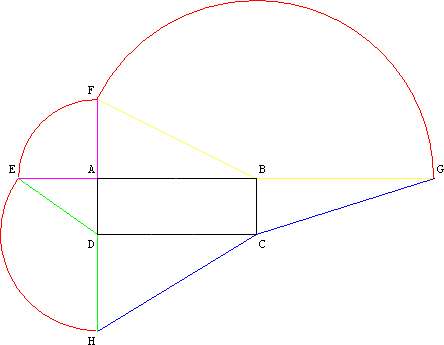
Les segments colorés par une même couleur sont de même longueur car ce sont des rayons des différents cercles
(,
et ).
L'image laisse alors apparaître le patron d'une pyramide à base rectangulaire ABCD de sommet S (E,F,B,H étant confondus en S).
En effet,
DE=DH donc H et E sont confondus en S
AE=AF donc E et F sont confondus en S
BF=BG donc F et G sont confondus en S
Ainsi H=E=F=G d'où G=H i.e. G et H sont confondus en S, ce qui permet de conclure que l'arête CS=CG=CH et l'égalité demandée.
Merci pour l'énigme puisea et merci également à infophile.
 CG2=BC2+BG2
CG2=BC2+BG2
BG=BF
BF2=FA2+AB2
donc
CG2=BC2+FA2+AB2
EA=FA et AD=BC et AB=DC
donc
CG2=AD2+EA2+DC2
AD2+EA2=ED2
ED=DH
donc
CG2=ED2+DC2=HC2
donc CG=HC
 Bonjour
Bonjour
AB = CD = a ; AD = BC = b ; AE = AF = µ
1)FAB est rectangle en A + Pythagore => BF² = a² + µ² = BG²
CBG ................ B ........... => GC² = a² + b² + µ² (1)
*
2)EAD ................ A ........... => DE² = b² + µ²
HDC ................ D ........... => HC² = a² + b² + µ² (2)
*
(1) et (2) => HC = GC
A+
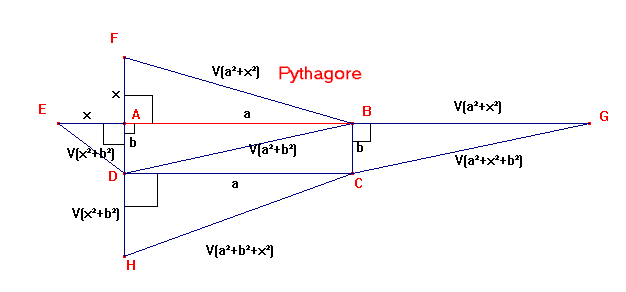
 Soient x la longueur AB du rectangle ABCD, y sa largeur AD et z le segment AE.
Soient x la longueur AB du rectangle ABCD, y sa largeur AD et z le segment AE.
Triangle rectangle AED : ED² = y²+z²; DH² = ED² = y²+z²
Triangle rectange DHC : HC² = DH²+x² = x²+y²+z²
Triangle rectangle AFB : AF = AE = z; FB² = x²+z² -> BG² = FB² = x²+z²
Triangle rectangle BGC : CG² = BG²+y² = x²+z²+y²
x²+z²+y² = HC² = CG²; HC = CG
On peut s'en rendre compte graphiquement :
Replions le triangle ADE perpendiculairement et au-dessus du plan du rectangle. Rabattons DCH de sorte que H coïncide avec E (possible car DH = DE et DE est maintenant perpendiculaire à DC). Imaginons le parallépipède dont la base est ABCD et E le sommet de la base opposée correspondant à A. DH (DE) est une diagonale de la face de gauche et CH (CE) est une grande diagonale.
Replions le triangle ABF perpendiculairement et au-dessus du rectangle. F coïncidera ave H et E. Rabattons BCG de sorte que G coïncide avec F (possible car BG = BF et BF et maintenant perpendiculaire à BC) BF (BG) est une diagonale de la face arrière et CG (CF) est la même grande diagonale que CH (CE).

 Salut à tous!
Salut à tous!
HC² = DH² + DC²
= DE² + DC² car DE = DH
Or : DE² = AD² + EA² et DC = AB
Donc :
HC² = AD² + EA² + AB²
Or : EA = AF
Donc :
HC² = AD² + AF² + AB²
= BC² + BF² car AD = BC et AF² + AB² = BF²
= BC² + BG² car BF = BG
= CG²
D'où : HC = CG
Merci pour l'énigme.

 Grâce à phytagore dans le triangle rectangle CGB.
Grâce à phytagore dans le triangle rectangle CGB.
CG²=BC²+FB².
FB²=AB²+AF².
donc:CG²=BC²+AB²+AF².
EA²=AF².
CG²=BC²+AB²+EA².
EA²=ED²-AD².
CG²=BC²+AB²ED²-AD².
ABCD est un rectangle: AD²=BC².
CG²=AB²+ED².
ED²=DH². donc CG²=AB²+DH².
DH²=HC²-DC².
CG²=AB²+HC²-DC².
DC²=AB².
FINALEMENT CG²=HC².
EN FIN :
CG=HC.
 En appliquant le théorème de Pythagore plusieurs fois
En appliquant le théorème de Pythagore plusieurs fois
CG^2=BC^2+BG^2=BC^2+BF^2=BC^2+AB^2+AF^2
CH^2=CD^2+DH^2=CD^2+DE^2=CD^2+AD^2+AE^2
et comme AD=BC , AB=CD et AE=AF, CG=CH
cqfd

 Bonsoir,
Bonsoir,
On peut le démontrer comme suit. On écrit la relation de pythagore pour chacun des triangles rectangles, ainsi que les égalités déduites des trois arcs de cercles. Je note L et l respectivement la longueur et la largeur du rectangle ABCD :
HC2 = HD2 + L2
HD2 = ED2
ED2 = EA2 + l2
EA2 = AF2
AF2 = FB2 - L2
FB2 = BG2
BG2 = CG2 - l2
En sommant les 7 égalités ci-dessus, les termes L2 et l2 s'éliminent, ainsi que tous les termes en italique. Reste HC2 = CG2, d'où HC = CG. CQFD.
Intuitivement, en se plaçant dans un espace à 3D la figure AFBGCHDE est le patron d'une pyramide ayant pour base le rectangle ABCD. Les points E, F, G et H se rejoignent à son sommet.
A++
 Nous avons :
Nous avons :
HC2
= DH2 + DC2 (Pythagore)
= DH2 + AB2 (Rectangle)
= DH2 - FA2 + FB2 (Pythagore)
= ED2 - EA2 + FB2 (Arcs de centres A et D)
= AD2 + FB2 (Pythagore)
= BC2 + BG2 (Rectangle + arc de centre B)
= CG2
Donc HC=CG.
Justin
 Bonjour,
Bonjour,
(HC)² = (DH)² + (DC)² pythagore HDC triangle rectangle en D
(HC)² = (DE)² + (DC)² cercle de centre D passant par H et E
(HC)² = (DA)² + (AE)² + (DC)² pythagore DAE triangle rectangle en A
(HC)² = (CB)² + (AE)² + (AB)² rectangle ABCD où DA=CB et DC=AB
(HC)² = (CB)² + (AF)² + (AB)² cercle de centre A passant par E et F
(HC)² = (CB)² + (BF)² pythagore BAF triangle rectangle en A
(HC)² = (CB)² + (BG)² cercle de centre B passant par F et G
(HC)² = (CG)² pythagore CBG triangle rectangle en B
d'où HC = CG
cqfd
Merci et à bientôt, KiKo21.
 Bonjour, à l'aide du théorème de pythagore, on a les relations suivantes :
Bonjour, à l'aide du théorème de pythagore, on a les relations suivantes :
HC²=DH²+DC² et CG²=BC²+BG²
Grâce à l'arc de cercle, on peut écrire BG=BF, soit BG²=BF² et ABCD étant un rectangle, on a BC=AD, soit BC²=AD².
On en déduit que CG²=AD²+BF², puis que CG²=AD²+AF²+AB² car BF²=AF²+AB².
On a (pour les même raisons que précédemment) AB=DC, soit AB²=DC² et AF=AE, soit AF²=AE² donc CG²=AD²+AE²+DC².
Il est clair que AD²+AE²=DE² et que DE=DH, soit DE²=DH² donc AD²+AE²=DH². On peut donc en déduire que CG²=DH²+DC², d'où CG²=HC², c'est-à-dire HC = CG. cqfd
Merci pour l'énigme ^^
 erreur de manipulation...
erreur de manipulation...
CG² = BG² + AD² = BF² + AD²
or AD² = ED² - EA² = DH² - AF²
donc CG² = BF² + DH² - AF²
CH² = DH² + AB²
or AB² = BF² - AF²
donc CH² = DH² + BF² - AF²
Donc CG² = CH²
Donc CG = CH

Notre ami Pythagore justifie qu'on puisse écrire :
et
.
On peut réécrire ces relations sous la forme :
et
.
On en déduit que : donc que
.
Là encore, Pythagore nous délivre, en affirmant que cela implique :
, càd que
Le compte est bon !
 Bonjour,
Bonjour,
On a les relations suivantes:
AD²+AE² = DE² (1)
DH²+DC² = CH² (2)
DH=DE, donc (2) devient:
DE²+DC² = CH² (3)
et d'après (1): AD²+AE²+CD² = CH² (3)
AB²+AF² = BF² (4)
AF=AE, donc (4) peut s'écrire:
AB²+AE² = BF² (5)
BC²+BG² = CG² (6)
BG=BF, donc (6) devient:
BC²+BF² = CG²
et d'après (5): BC²+AB²+AE² = CG² (7)
Comme AD=BC et CD=AB, (7) devient AD²+CD²+AE² = CG² (8)
En comparant (3) et (_) on a CH² = CG², d'où HC = CG, CQFD.
A+,
gloubi
 On utilise le théorème de Pytagore et le fait que les rayons d'un même cercle ont tous même longueur.
On utilise le théorème de Pytagore et le fait que les rayons d'un même cercle ont tous même longueur.
or HE=DE
or
donc
cqfd

 Bonjour,
Bonjour,
Voici ma proposition, en utilisant le théorème de Pythagore :
HC² = DH² + DC²
= DE² + AB²
= DA² + AE² + AB²
= BC² + AF² + AB²
= BC² + FB²
= BC² + BG²
= CG²
Donc HC² = CG²
Soit HC = CG
Merci pour cette énigme.
 la figure et ses indications nous permettent de montrer que :
la figure et ses indications nous permettent de montrer que :
ED^2 = AD^2 + AE^2 =) DH^2 = AD^2 + EA^2 =) DH^2 = BC^2 + FA^2.
De même, DC^2 = FB^2 - FA^2 =) DC^2 = GB^2 - FA^2.
=) DH^2 + DC^2 = GB^2 + BC^2.
=) HC = GC




 Bonjour,
Bonjour,
-Dans le triangle HCD rectangle en D, d'après le théorème de Pythagore on a: HC²=HD²+DC² et comme HD= ED et DC= AB, alors: HC²= ED²+AB² (1).
- Dans le triangle AED rectangle en A, d'après le théorème de Pythagore ED²=AE²+AD² (2)
- Dans le triangle ABF rectangle en A, d'après le théorème de Pythagore BF²=AF²+AB², d'où AB²=BF²-AF² (3)
- En remplaçant dans (1) les égalités (2) et (3) on obtient: HC²=AE²+AD²+BF²-AF² et comme AE=AF, alors HC²=AD²+BF² (4) et comme AD= BC et BF=BG, en remplaçant dans (4) on obtient: HC²= BC²+ BG² (5).
- Dans le triangle BCG rectangle en B, d'après le théorème de Pythagore: BC²+ BG²= CG², en remplaçant dans (5) on obtient: HC²= CG², d'où HC= CG (puisque HC et CG sont des réels positifs).
 HC²
HC²
= HD² + DC² (Pythagore dans HCD)
= DE² + DC² (E et H sont sur le même cercle de centre D)
= DA² + AE² + DC² (Pythagore dans EAD)
= DA² + AF² + DC² (E et F sont sur le même cercle de centre A)
= DA² + AF² + AB² (car DC = AB dans le rectangle ABCD)
= DA² + BF² (Pythagore dans AFB)
= BC² + BF² (car DA = BC dans le rectangle ABCD)
= BC² + BG² (F et G sont sur le même cercle de centre B)
= CG² (Pythagore dans BCG)
Donc HC = CG
 Bonjour, et merci pour l'énigme.
Bonjour, et merci pour l'énigme.
Analysons les deux cotes CG et HC
CG²=BC²+BG² (pythagore dans le triangle BCG)
CG²=BC²+BF² (BG=BF suite à l'arc de centre B)
CG²=BC²+(FA²+AB²) (Pythagore sur BF dans le triangle ABF)
donc on a CG²=BC²+FA²+AB².
HC²=DC²+DH² (pythagore dans le triangle HDC)
HC²=AB²+DE² (Comme ABCD rectangle, DC=AB et DH=DE suite à l'arc de centre D)
HC²=AB²+(EA²+AD²) (pythagore sur DE dans le triangle EAD)
HC²=AB²+FA²+AD² (EA=FA suite a l'arc de centre A)
HC²=AB²+FA²+BC² (Comme ABCD rectangle, AD=BC)
donc on a HC²=BC²+FA²+AB²
On en déduit que HC²=CG² donc comme il s'agit de longueurs donc de mesures positives HC=CG, cqfd
A bientôt
 HC² = DH² + CD² d'après Pythagore dans CDH
HC² = DH² + CD² d'après Pythagore dans CDH
GC² = BC² + BG² d'après Pythagore dans BCG
GC² = BC² + BG²
= BC² + BF² dans le cercle de centre B
= BC² + AF² + AB² d'après Pythagore dans ABF
= BC² + AE² + CD² dans le cercle de centre A
= AD² + AE² + CD²
= ED² + CD² d'après Pythagore dans ADE
= DH² + CD² dans le cercle de centre D
GC² = HC²
Donc GC = CH.
 Les droites (AB) et (BG) sont confondues, de plus les droites (AB) et (BC) sont perpendiculaires. Donc les droites (BC) et (BG) sont perpendiculaires.
Les droites (AB) et (BG) sont confondues, de plus les droites (AB) et (BC) sont perpendiculaires. Donc les droites (BC) et (BG) sont perpendiculaires.
D'après le théorème de Pythagore, dans le triangle BCG, on peut donc écrire l'égalité suivante :
CG[/sup]2 = BG[sup]2 + BC[/sup]2
Les segments [BG] et [FB] appartiennent au même arc, alors BG = FB donc BG[sup]2 = FB[/sup]2
Donc CG[sup]2 = FB[/sup]2 + BC[sup]2
Les droites (AD) et (AF) sont confondues, de plus les droites (AB) et (AD) sont perpendiculaires. Donc les droites (AB) et (AF) sont perpendiculaires.
D'après le théorème de Pythagore, dans le triangle ABF, on peut donc écrire l'égalité suivante :
FB[/sup]2 = FA[sup]2 + AB[/sup]2
Donc CG[sup]2 = AF[/sup]2 + AB[sup]2 + BC[/sup]2
Les droites (AD) et (DH) sont confondues, de plus les droites (AD) et (DC) sont perpendiculaires. Donc les droites (DH) et (DC) sont perpendiculaires.
D'après le théorème de Pythagore, dans le triangle CDH, on peut donc écrire l'égalité suivante :
CH[sup]2 = DC[/sup]2 + DH[sup]2
Les segments [DH] et [ED] appartiennent au même arc, alors DH = ED donc DH[/sup]2 = ED[sup]2
Donc CH[/sup]2 = DC[sup]2 + ED[/sup]2
Les droites (EA) et (AB) sont confondues, de plus les droites (AD) et (AB) sont perpendiculaires. Donc les droites (AD) et (EA) sont perpendiculaires.
D'après le théorème de Pythagore, dans le triangle ADE, on peut donc écrire l'égalité suivante :
ED[sup]2 = EA[/sup]2 + AD[sup]2
Donc CH[/sup]2 = DC[sup]2 + EA[/sup]2 + AD[sup]2
Les côtés opposés d'un triangle sont deux à deux de même longueur:
donc AB = DC et AB[/sup]2 = DC[sup]2
et BC = AD et BC[/sup]2 = AD[sup]2
Donc CH[/sup]2 = AB[sup]2 + EA[/sup]2 + BC[sup]2
Les segments [AF] et [EA] appartiennent au même arc, alors AF = EA donc AF[/sup]2 = EA[sup]2
Donc [i]CH[/sup]2 = AB[sup]2 + AF[/sup]2 + BC[sup]2 = CG[sup][/sup]2
Donc les droites (CH) et (CG) sont de même longueurs.[/i]
 Bonjour à tous,
Bonjour à tous,
Voici ma réponse dans laquelle je reprends les dénominations des points, segments, etc, de la figure jointe à l'énoncé.
Nous avons (FB)=(BG) comme rayons du même cercle de centre B;
(AE)=(AF) comme rayons du même cercle de centre A;
(DH)=(DE) comme rayons du même cercle de centre D.
Par hypothèse (ABCD) est un rectangle:
d'où (AD)=(BC);
(AB)=(DC)
les angles A,B,C,D sont droits et les triangles
(BAF), (BAD), (DAE), (BCD), (HDC) et (CBG) sont
rectangles.
Selon les égalités et les déductions qui précèdent, et en appliquant aux triangles rectangles le théorème de Pythagore, nous avons:
(HC)²=(HD)²+(DC)²
=(DE)²+(AB)²
=(AE)²+(AD)²+(AB)²
=(AF)²+(AD)²+(AB)²
=(FB)²-(AB)²+(AD)²+(AB)²
=(FB)²+(AD)²
(CG)²=(BC)²+(BG)²
=(AD)²+(FB)²
=(AD)²+(AF)²+(AB)²
=(AD)²+(FB)²-(AB)²+(AB)²
=(FB)²+(AD)².
Des égalités qui précèdent, nous déduisons que:
(HC)²= (CG)² = (FB)² + (AD)²
d'où (HC)²= (CG)²
et .

 Bonjour,
Bonjour,
D'après la figure, comme ABCD est un rectangle, on a :
- les triangles ABF, AEF et ADE sont rectangles en A,
- le triangle CDH est rectangle en D
- et le triangle BCG est rectangle en B
Donc, grâce à Pythagore, on a les égalités suivantes qui nous seront utiles :
- BF²=AF²+AB², DE²=AD²+AE²
- HC²=CD²+DH²
- et CG²=BC²+BG²
Par ailleurs, on a des arc de cercle qui nous permettent d'écrire que
DH=DE, AE=AF, BF=BG
Et enfin on sait que le quadrilatère ABCD est rectangle donc AB=CD et AD=BC
Ainsi on peut écrire
HC²=CD²+DH²
HC²=AB²+DE² car AB=CD et DE=DH
HC²=AB²+AE²+AD² car DE²=AD²+AE²
HC²=AB²+AF²+BC² car AE=AF et AD=BC
HC²=BF²+BC² car BF²=AF²+AB²
HC²=BG²+BC² car BF=BG
HC²=CG² car CG²=BC²+BG²
d'où HC=CG car ce sont des longueurs donc elles sont positives.

 translation: DBCH est un parallelogramme donc HDC est l'image de CBG par la translation qui transforme B en D. or, dans un translation les mesures se conservent donc HC=CG
translation: DBCH est un parallelogramme donc HDC est l'image de CBG par la translation qui transforme B en D. or, dans un translation les mesures se conservent donc HC=CG
 Bonjour,
Bonjour,
Tout d'abord, on peut se demander si certains triangles sont rectangles... comme BCG ou AFB.
Alors en fait, j'ai essayé de changer les arcs pour voir et l'égalité qu'on voulait démontrer n'était plus vérifiée. Donc j'ai supposé que ces triangles étaient rectangles.
D'aprés Pythagore dans DCH,
on a HC²=HD²+DC² (2)
Et dans BGC on a:
CG²=BG²+BC² (1)
Or on a aussi:
BG=BF car F et G appartienne au cercle de centre B
Et dans le triangle AFB, on a, grace à Pythagore:
BF²=AB²+AF² ,et donc par transition:
BG²=AB²+AF²
De plus BC=AD ( car ABCD est un rectangle) donc BC²=AD²
Ainsi (1) <=> CG²= AB²+AF²+AD²
Ensuite,
On a : HD=DE E et H appartienne tout deux au cercle de centre D
soit HD²=DE² et DC=AB soit DC²=AB²
Ainsi (2) <=> HC²= DE²+AB²
Or Dans le triangle AED on a, d'aprés Pythagore:
DE²=AE²+AD²
Ainsi: (2) <=> HC²= AB²+AE²+AD²
Donc:
Ainsi (1) <=> CG²= AB²+AF²+AD²
et (2) <=> HC²= AB²+AE²+AD²
Sachant que AF=AE car E et F appartiennent tout deux au cercle de centre A, on trouve bien l'égalité cherchée qui est:
HC²=CG² soit HC=CG ( EE HC et CG > 0 )
Merci pour l'énigme
Sticky

 Si nous voulons nous en tenir à un niveua expérimental. Opérons une impression du fichier image. Mesurons les deux segments en question. Là, nous constatons que les deux segments ont même longueur, en l'occurence environ 5.2 cm pour l'échelle que mon imprimante à choisi. Donc si la norme de HC est égal à la norme de CG, ces deux segments ont même longeur.
Si nous voulons nous en tenir à un niveua expérimental. Opérons une impression du fichier image. Mesurons les deux segments en question. Là, nous constatons que les deux segments ont même longueur, en l'occurence environ 5.2 cm pour l'échelle que mon imprimante à choisi. Donc si la norme de HC est égal à la norme de CG, ces deux segments ont même longeur.

 |DG|²=|BG|²+|BD|² --> |BG|=|FB| et |FB|²=|FA|²+|AB|² remplaçons |FB|--> |DG|²=|FA|²+|AB|²+|BD|²
|DG|²=|BG|²+|BD|² --> |BG|=|FB| et |FB|²=|FA|²+|AB|² remplaçons |FB|--> |DG|²=|FA|²+|AB|²+|BD|²
|DH|²=|CH|²+|CD|² --> |CH|=|EC| et |EC|²=|EA|²+|AC|² remplaçons |EC|--> |DH|²=|EA|²+|AC|²+|CD|²
si on compare les deux dernières formules
|FA|=|EA| et |AB|=|CD| et |BD|=|AC| DONC |DG| EST BIEN EGALE A |DH|
 Bonjour,
Bonjour,
ABCD étant un rectangle, nous avons les égalités suivantes :
AB = CD
AD = BC
De plus, F, A, D et H étant alignés et ABCD étant un rectangle, nous avons FAB rectangle et A et HDC rectangle en D. On peut donc appliquer le théorème de Pythagore à ces triangles :
FB2 = FA2 + AB2
HC2 = HD2 + DC2
De même, E, A, B et G étant alignés et ABCD étant un rectangle, nous avons DAE rectangle et A et CBG rectangle en D. On peut donc appliquer le théorème de Pythagore à ces triangles :
DE2 = DA2 + AE2
CG2 = CB2 + BG2
Enfin, HD et DE étant rayons d'un même arc, HD = DE.
Pour la même raison, EA = AF et FB = BG.
Bien, munis de toutes ces relations, nous pouvons nous lancer dans le la démonstration demandée :
HC2 = HD2 + DC2
= DE2 + AB2
= DA2 + AE2 + AB2
= BC2 + AF2 + AB2
= BC2 + FB2
= BC2 + BG2 = CG2
Voilà !
Merci pour le challenge.
Merci à tous de votre participation.
Vous auriez pu démontrer l'égalité en disant plus simplement que la figure était le patron d'une pyramide.
@+
Nombre de participations : 0
Temps de réponse moyen : 29:20:01.