Bonjour,

l'aire de la partie grisée est toujours égale à 1 cm² (merci geoplan)

Salut

     soit C1 l'aire du carre initiale.
  alors, l'aire C2 commune au 2 carre est:
    C2= C1:4      

Salut,
on peut obtenir assez facilement que cette aire ne varie pas en fonction de la position du second carré, ainsi il suffit de calculer l'aire de l'intersection des carrés lorsque celle ci représente un carré de côté 1cm cad lorsque les côtés du second carrés sont parrallèlle 2 à 2 avec ceux du premier.
Ainsi on obtient une aire de 1cm²

en prenant le cas particulier ou les deux cotés du triangle passent par les milieux des cotés du second, on trouve facilement que A=1 cm².

L'aire commune à ces 2 carré est 1 [cm^2]

En effet, de par la symétrie du problème, on voit que l'aire commune ne dépends pas de l'inclinaison du carré et vaut 1/4 de l'aire du carré, soit (c^2)/4 = (2*2)/4 = 1 [cm^2]

L'aire commune a ces 2 carrés est de 1 cm^2

On sait que les angles d'un carré sont de 90°, comme un sommet du 2ème carré est au centre de gravité de l'autre carré, la surface commune vaut 1/4 de la surface du carré.
Si on prend 4 surfaces comme la surface commune, on peut reconstituer un carré.

je dirais 1 cm²

/4 d el'aire du carré
donc aire carré:
2*2=4
La'iare commune est 1cm²

je dirai 2*2=4(aire total d'un carré

si on tourne le second carré afin que les 2 cotés du carré coupe les sommet de l'autre carré on obtient un triangle que l'on peut recopier 3 fois dans le carré de départ d'où l'aire commune = 1 cm²

bonjour !

la surface en commun aux deux carrés est
1cm²

Bonjour

1 cm²

Lorsue l'on considère images de la figure grisée par les rotations centrées sur le centre du premier carré et d'angle respectivement 0,, et , on obtient un recouvrement du carré sans chevauchement. L'aire de la figure grisée correspond donc au quart du carré soit 1 cm²

Bravo !! beaucoup de réussite !!

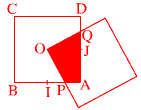
Notons ABCD le premier carré et O son centre, le point A étant l'un des sommets du polygone grisé qui est alors OPAQ.
Notons I et J les milieux respectifs des côtés AB et AD. Sans nuire à la généralité, on peut supposer que P est sur (IA) et Q sur (JD). Dans ce cas, on voit que OPAQ a la même aire que le carré OIAJ, car les triangles OIP et OJQ sont isométriques.
Et l'aire OIAJ est le quart de l'aire de Abcd, soit 1 cm².



Prochaine énigme déja " dans les bacs "