Inscription / Connexion Nouveau Sujet
Challenge n°33

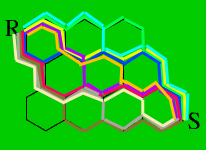
Combien y a-t-il de plus courts chemins suivant les lignes du réseau et allant de R à S ?
Bonne chance 
 Après un petit dénombrement je dirai qu'il y a 20 chemin de longueur 11 en ayant pour unité la longueur d'un des côtés des du pavé(hexagone)formant le réseau
Après un petit dénombrement je dirai qu'il y a 20 chemin de longueur 11 en ayant pour unité la longueur d'un des côtés des du pavé(hexagone)formant le réseau
Et que 11 est la taille du chemin le plus court


 Salut!
Salut!
Je dirais 5.
J'suis pas sûre mais au moins j'aurais essayer.



 Bonsoir
Bonsoir
Si on compte seulement 5 images de R à S, je trouve qu'il y a que 5 chemins au plus court
Mais euhh on verra à la correction 
A+


coucou !
alors c'est vraiment casse tete tout ca !
si je ne me suis pas trompée il y en a 14
(je croise les doigts .. ca sent le poisson)
J'aurais tenté 
ciao


 re
re
j'suis trop bete  j'crois que j'en ai oublier une
j'crois que j'en ai oublier une  . Bon c'est pas grave j'ferai + attention la prochaine fois.
. Bon c'est pas grave j'ferai + attention la prochaine fois. 


 Il y à 9 noeuds où 2 chemins sont possibles (pour avoir un chemin de longueur minimale = 11), donc je dirais qu'il y a 2^9 = 512 plus courts chemins...
Il y à 9 noeuds où 2 chemins sont possibles (pour avoir un chemin de longueur minimale = 11), donc je dirais qu'il y a 2^9 = 512 plus courts chemins...


 oups, grossière erreur de ma part, il fallait additionner plustot que multiplier, ça donnerait donc 2 * 9 = 18
oups, grossière erreur de ma part, il fallait additionner plustot que multiplier, ça donnerait donc 2 * 9 = 18
(ça commence à sentir le poisson...)


 On peut voir le shéma comme un arbre, à chaque intersection, il y a 2 chemins possible ... je pense qu'il y a 2^4 = 32 chemins ...
On peut voir le shéma comme un arbre, à chaque intersection, il y a 2 chemins possible ... je pense qu'il y a 2^4 = 32 chemins ...
 Les plus courts chemins sont au nombre de 20
Les plus courts chemins sont au nombre de 20
En effet ces plus courts chemins sont composés de 11 segments, 3, 5
et 3
, les 5 flèches
occupant les positions paires dans les séquences de 11 segments. (par exemple :
constitue un plus cout chemin). Il faut donc répartir les 3
et les 3
sur les 6 emplacements de rang impair soit
possibilités (tous les séquences de chemins étant possibles).


 alors moi je dirais qu'il y a 10 soulution voila la preuve
alors moi je dirais qu'il y a 10 soulution voila la preuve
 Salut à tous
Salut à tous  ,
,
Ma réponse est : il existe 20 plus courts chemins possibles pour aller de R à S.
Raisonnement
*Simplification du schémas :
On remarque tout d'abord que ce schémas est constitué de 10 hexagones qui ont des côtés en commun. Il est facile de se rendre compte que aucun plus court chemin ne passe par les côtés qui appartiennet seulement à l'hexagone le plus en bas à gauche.
1ère Conclusion : On peut déjà alléger le schémas en supprimant les 4 côtés qui appartiennent seulement à l'hexagone en bas à gauche. On se retrouve alors avec un schémas constitué de 9 hexagones.
Il est impossible d'expliquer trop détaillemment ce qui va suivre, sinon je ne le rendrai que plus compliqué  . Il faut se rendre compte que ce shémas de 9 hexagones peut en fait se résumer à un quadrillage de 3*3 dans lequel, si on veut emprunter le plus court chemin, on a uniquement droit à chaque intersection, à faire un pas vers le bas ou vers la doite (condition nécessaire pour que le chemin emprunté soit l'un des plus courts
. Il faut se rendre compte que ce shémas de 9 hexagones peut en fait se résumer à un quadrillage de 3*3 dans lequel, si on veut emprunter le plus court chemin, on a uniquement droit à chaque intersection, à faire un pas vers le bas ou vers la doite (condition nécessaire pour que le chemin emprunté soit l'un des plus courts  )
)
2ème Conclusion : Ce schéma peut ainsi se réduire à un quadrillage de 3 carreaux par 3, où R serait le point de coordonnée (0,0), et S celui de coordonnées (-3,-3).
*Calcul du nombre de possibilités de plus courts chemins possibles :
Sur notre nouveau schémas, on se rend compte que les plus courts chemins sont tous de 6 pas, dont 3 sont vers la droite et 3 vers le bas.
Ainsi, parmis nos 6 pas, il faut choisir les 3 que l'on fera vers la droite, et les 3 que l'on fera vers le bas  , Par exemple, on peut choisir le chemin {B,B,B,D,D,D} ou encore {B,D,B,D,B,D} qui ne sont que deux des multiples possibilités de chemins plus court qu'il nous faut calculer.
, Par exemple, on peut choisir le chemin {B,B,B,D,D,D} ou encore {B,D,B,D,B,D} qui ne sont que deux des multiples possibilités de chemins plus court qu'il nous faut calculer.
On remarque que le chemin est à lui seul déterminer par la "place" des 3 pas que l'on fait vers la droite (puisque si on ne fait pas un pas vers la droite, on doit le faire ves le bas).
Par exemple, il suffit de dire : mon premier, mon troisième et mon quatrième pas vers la droite, pour en déduire que le second, le cinquième et le sixième pas seront faits vers le bas, ce qui nous donnera le chemin {D,B,D,D,B,B}.
Ainsi, le nombre de plus courts chemins possible correspond au nombre de combinaisons de 3 objets (à savoir les 3 pas vers la droite -on aurait pu aussi choisir les pas vers le bas, en raison de la "symétrie" de la formule des combinaison, càd que -), parmis 6 (qui sont les 6 pas à faire).
Le nombre de plus courts chemins possibles est donc égal à :
d'où
càd
donc
CONCLUSION : On a un total de 20 plus courts chemins possibles.
Voili, voilou  .
.
Bonne chance à tous  , et merci à Puisea pour cette énigme
, et merci à Puisea pour cette énigme 
En espérant avoir juste  ,
,
À + 
Je suis très content mes espoirs de devenir un jour poissonnier se sont vus grandir  Bravo à tous d'avoir particper, voici une maigre correction qui peut être développée comme l'a si bien démontrer Belge-FDLE
Bravo à tous d'avoir particper, voici une maigre correction qui peut être développée comme l'a si bien démontrer Belge-FDLE 
A chaque sommet du pavage hexagonal, on associe le nombre de plus courts chemins allant de R à ce sommet.
On calcule ce nombre de proche en proche à partir de R.
On trouve 20 en arrivant à S.
En image :


 Bonjour
Bonjour 
Tant pis j'ai tenté ma chance puis ce n'est qu'un jeu amical histoire de passer le temps et de s'amuser puis l'important c'est de participer 
Bisous à tous 
A+
Nathalie 
je me permets d'intervenir puisea,
il y a une chose super improtante en jeu, ce son les poissons 
non, sérieusement, ce genre d'énigmes, permets d'apprendre à raisonner, à force d'en faire, on raisonne plus vite.
cela peut aider même en dehors des maths 
ciao 
Nombre de participations : 0
Temps de réponse moyen : 13:31:58.


