Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques DétentePour discuter des JFF, des problèmes intéressants. ExercicesExercices ludiques [tout]Lister tous les topics de mathématiques
Niveau exercices
Partager :

Collision

Posté par
flight 24-08-23 à 20:28

Bonsoir

je vous propose l'exercice sympathique qui suit :

on se donne 10 cases alignées ( horizontalement) et numerotées de 1 à 10 , à l'instant t=0 , un robot noté "A" se trouve dans la case 1 , tandis qu'un robot noté "B " se trouve à la case 10.
A chaque seconde, soit le robot A reste dans la case qu'il occupe avec une probabilité de 3/7 , soit il avance d'une case avec une probabilité de 4/7.
A chaque seconde  , soit le robot B reste dans la case qu'il occupe avec une probabilité de 3/8 , soit il avance d'une case avec une probabilité de 5/8.
d'apres vous , en moyenne ,au bout de combien  de temps les robots A et B se trouveront ils dans la même case ou dans deux cases adjacentes ?   (en effet si A se trouve en 2 et B en 5 , si ils se deplacent tout les deux alors ils occuperont des cases voisines , par contre si A est en 2 et B en 4 et qu'ils se déplacent tout les deux alors ils se trouveront dans la case 3 ensemble)

Posté par
flightre : Collision 24-08-23 à 23:03

precision  : les robots A et B sont actifs  à l'instant t = 0

Posté par
Leilere : Collision 24-08-23 à 23:55

bonsoir flight

 Cliquez pour afficher

Posté par
flightre : Collision 25-08-23 à 16:19

Bonjour Leile c'est bien ca , mais tu n' a pas exposé ta methode

Posté par
flightre : Collision 25-08-23 à 16:20

(j'aurai du ajouter une precision : A va vers B et B vers A )

Posté par
carpediemre : Collision 25-08-23 à 16:46

salut

vu qu'il y a indépendance la probabilité que :

A et B avancent d'une case est 10/28 = 20/56
un seul des deux avance d'une case est 27/56
aucun n'avance est 9/56

on en revient alors au pb suivant : un mobile A se déplace de la case 1 à la case 10 avec les probabilités 9/65 (resp. 27/56 et 20/56) de se déplacer de 0 (resp. 1 et 2) case(s)

en moyenne combien de déplacements met-il pour atteindre au moins la case 9 ?

puisque tu demandes quand les mobiles seront sur la même case ou dans des cases adjacentes

en appliquant la classique règle qu'on ajoute les vitesses quand deux mobiles se percutent ...


enfin y a-t-il réellement équivalence entre ces deux problèmes ?

Posté par
verdurinre : Collision 25-08-23 à 22:03

Bonsoir,
la distance de départ entre les deux robots est de 9 cases.

En moyenne elle diminue de \frac47\times1+\frac58\times 1=\frac{67}{56} chaque seconde.

J'ai tendance à penser que pour qu'elle devienne inférieure ou égale à 1 il faudra en moyenne  \frac{67}{56}\times 8 secondes.

Posté par
verdurinre : Collision 25-08-23 à 22:27

Ceci étant j'ai fait une simulation qui me donne tort.

Posté par
verdurinre : Collision 25-08-23 à 22:41

Ce qui est évident car le résultat de mon raisonnement est 8\div\frac{67}{56}.
Mais ça ne colle toujours pas à la simulation.
Je vais dormir.

Posté par
LittleFoxre : Collision 26-08-23 à 10:56


Soit t(n) le temps moyen avant la collision si les (centre des) robots sont distant de n.

On a t(0) = t(1) = 0. On cherche t(9).
On a t(n+2) = 1 + t(n+2) (3/7*3/8) + t(n+1) (4/7*3/8+3/7*5/8) + t(n)(4/7*5/8). On passe t(n+2) à gauche et on calcule.

 Cliquez pour afficher


On obtient t(9) = \frac{165150267208864}{23811286661761} \approx 6.935797697739785

Posté par
dpire : Collision 26-08-23 à 11:12

Bonjour,

 Cliquez pour afficher

Posté par
Imodre : Collision 26-08-23 à 11:30

Bonjour

Oui LittleFox , l'idée est exactement la même que celle développée par Jandri dans Déplacements .

Imod

Posté par
LittleFoxre : Collision 26-08-23 à 12:19

@Imod
Oui, je sais. J'ai pas mal cogité sur cette énigme aussi.

@verdurin
L'idée est bien là. On a bien qu'à la limite, le temps pour se rapprocher d'une case est de 56/67s. Reste à trouver le temps zéro.
Tous calculs fait on a t(n) \approx \frac{56}{67}(n - \frac{47}{67}) . L'erreur diminue très vite (facteur 20/47) et on est à moins de 1% d'erreur pour n > 4.

@dpi
Il y a un problème dans ta simulation
La vitesse moyenne est de \frac{67}{56} \approx 1.196 case/s

@carpediem
Le problème n'est pas tout à fait équivalent car on ne sait pas à priori les probabilités que les robots s'arrêtent sur la même case où sur des cases adjacentes.
Mais je suis d'accord que c'est équivalent à un seul mobile A qui se déplace. Mais depuis la case 9 vers 0 ou 1 et pas l'inverse.

Posté par
carpediemre : Collision 26-08-23 à 13:44

merci LittleFox mais je pense que

LittleFox @ 26-08-2023 à 12:19

Le problème n'est pas tout à fait équivalent car on ne sait pas à priori les probabilités que les robots s'arrêtent sur la même case où sur des cases adjacentes.
ne dépend que d'un simple pb d'orientation et d'origine des déplacements :qu'on parte de 10 pour atteindre 1 ou 2 ou de 1 pour atteindre 9 ou 10 (ou en retranchant si on prend pour origine 0) n'est-ce pas la même chose ?

verdurin @ 25-08-2023 à 22:03

En moyenne elle diminue de \frac47\times1+\frac58\times 1=\frac{67}{56} chaque seconde.
n'aurais-tu pas oublier le déplacement possible de 2 cases dans ton calcul de déplacement moyen ?

Posté par
LittleFoxre : Collision 26-08-23 à 14:06

@carpediem
Oui, OK. Je disais que partir de 1 ou 2 pour atteindre 10 n'est pas équivalent à partir de 10 pour atteindre 1 ou 2.

Le calcul de verdurin est correct, la moyenne de la somme est bien la somme des moyennes. Si tu veux expliciter le déplacement de deux cases alors on a:

\frac{3}{7}\frac{3}{8} \times 0 + \frac{3}{7}\frac{5}{8} \times 1 + \frac{4}{7}\frac{3}{8} \times 1 + \frac{4}{7}\frac{5}{8} \times 2 = \frac{3}{7}\frac{5}{8} \times 1 +  \frac{4}{7}\frac{5}{8} \times 1 + \frac{4}{7}\frac{3}{8} \times 1 + \frac{4}{7}\frac{5}{8} \times 1 =  (\frac{3}{7} +  \frac{4}{7}) \frac{5}{8} \times 1 +  \frac{4}{7}(\frac{3}{8}+}\frac{5}{8} ) \times 1 =  \frac{5}{8} \times 1 +  \frac{4}{7} \times 1  

Posté par
carpediemre : Collision 26-08-23 à 14:15

ok d'accord !

ok d'accord bis !

n'ayant pas explicité  son calcul comme ton premier membre (tout comme moi) j'ai pensé que verdurin eut pu faire une "bête" erreur de calcul de moyenne ...  

Posté par
flightre : Collision 26-08-23 à 19:20

Bonjour

en faisant tourner un bout de code on arrive precisement à quelques chose comme 6,9 secondes .
j'ai pas été plus précis que vous autres  dans le calcul , j'ai eu une approche "simplifiée "
je note T le temps necessaire que A se retrouve adjacent à B  
je note aa la V.A nombre d'avances de A , sa la V.A nombre d'arrets ou stops de A.
je note ab la V.A  nombre d'avances de B , sb la V.Anombre d'arrets ou stops de B.
dans le cas " rencontre avec cases adjacentes " on a  
aa + ab=8  
on a aussi : aa + sa=T ( temps ecoulé jusqu'a la recontre  et  aussi ab + sb=T.
en passant par l'espérance il vient E(aa)+E(ab)=8   soit  (4/7)T+ (5/8)T= 8
ce qui donne  T (de collision en cases adjacentes)=6,6866

Dans le cas ou les robots se retrouvent dans la meme case on a  :

aa + ab=9
on a aussi : aa + sa=T ( temps ecoulé jusqu'a la recontre  et  aussi ab + sb=T.
en passant par l'espérance il vient E(aa)+E(ab)=9   soit  (4/7)T+ (5/8)T= 9
ce qui donne  T (de collision en case identiques)=7,5224

je fais la moyenne des deux resultats obtenus et ca donne  7,10 s

c'est pas si precis que ca ....

Posté par
Leilere : Collision 26-08-23 à 20:37

flight @ 25-08-2023 à 16:19

Bonjour Leile c'est bien ca , mais tu n' a pas exposé ta methode


hello flight,
j'ai aussi écrit un bout de code très simple, je tourne tant que (xB - xA) est > 1.
Sur un grand nombre de fois, la moyenne = 7.

Posté par
Leilere : Collision 26-08-23 à 20:38

Il me semble qu'i faut donner un nombre entier de secondes, puisque les déplacements se font seconde par seconde, et en même temps.

Posté par
dpire : Collision 27-08-23 à 07:40

Bon dimanche,
La remarque de Leile  permet bien d'arrondir  à 7 s.
En effet au même dénominateur 56 on  a bien 32avancées pour A
et 35 pour B (j'avais une grosse erreur dans ma simulation d'hier...)
7.522  arrondi  par le bas donne 7 s

Posté par
Imodre : Collision 27-08-23 à 11:01

Pourquoi arrondir à l'unité ? Quand on fait une moyenne de notes entières , le résultat doit-il être entier ? Le temps moyen est de \dfrac{448}{65}\approx 6,89 \text{ s} .
Imod

Posté par
LittleFoxre : Collision 27-08-23 à 11:41

@Leile
Non, il n'y a aucune raison que la moyenne de nombres entiers soit entière.
Si on calculait le mode (la valeur la plus fréquente) alors oui ce serait entier. Mais c'est un tout autre calcul.

@Imod
D'où vient ton 448/65? J'ai une réponse différente.

@flight
Non, on ne peut pas faire la moyenne des deux cas. Ils arrivent à des fréquences différentes. Voir mes réponses à carpediem.
Je suis d'accord que la valeur se trouve entre les deux mais on ne sait dire à priori où entre les deux.
De plus, la condition aa + ab = 8 change la probabilité d'avancer et E(aa). La probabilité d'avancer pour a n'est plus indépendante de la probabilité pour b.

Posté par
Imodre : Collision 27-08-23 à 11:57

Faute de frappe \dfrac{448}{67}\approx 6,69\  .

Pour en revenir aux moyennes , imaginons que l'on analyse le taux de natalité en Europe en arrondissant à l'unité ... Et pourtant personne ne fabrique des morceaux d'enfants

Imod

Posté par
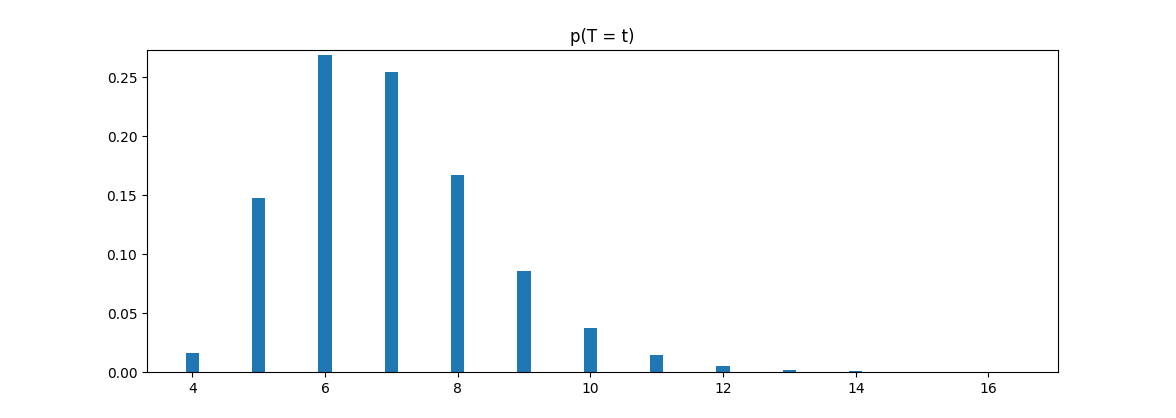
LittleFoxre : Collision 27-08-23 à 12:09

Voici un graphique de la distribution de t pour n=9. On voit que le mode est 6 (plus haute barre) pourtant la moyenne est plus proche de 7.
Notez que le minimum est t=4, alors qu'il n'y a pas de maximum (mais la probabilité diminue exponentiellement quand t devient grand).

Collision

Posté par
Imodre : Collision 27-08-23 à 12:50

Je ne me suis jamais vraiment intéressé au probas et je fais certainement une erreur de logique . Voilà comment j'avais vu les choses :

Au départ l'écart entre les deux robots est de 8 cases et à chaque seconde cet écart se réduit en moyenne de \dfrac{27}{56}+2.\dfrac{20}{56}=\dfrac{67}{56}\  . On cherche à partir de quel temps T cet écart sera au plus nul : 8-T.\dfrac{67}{56}\leq 0\ . On arrive au résultat annoncé \dfrac{448}{67}\ .

Imod


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !