Inscription / Connexion Nouveau Sujet
Configurations premières principales d'un rectangle
Je vous propose le problème suivant:
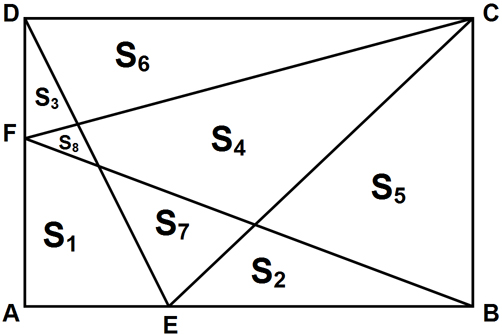
ABCD est un rectangle tel que AB ≥ AD. AB, AD, AE et AF sont des longueurs entières.
a) Une configuration est dite première lorsque les 8 surfaces Si (i = 1, 2, ..., 8) sont entières et premières entre elles (globalement et pas deux à deux).
b) Deux configurations premières G et G' sont dites équivalentes si : {S'1, S'2, S'3, S'4, S'5, S'6, S'7, S'8} = {S1, S2, S3, S4, S5, S6, S7, S8} (on parle bien d'ensembles).
c) Parmi un ensemble de configurations premières équivalentes, on convient d'appeler configuration principale celle telle que AB est minimal (ce qui revient à choisir celle de périmètre minimal ou encore celle se rapprochant le plus d'un carré...).
Exemples:
1) (AB, AD, AE, AF) = (10, 6, 5, 3) est la plus petite configuration principale, avec : (S1, S2, S3, S4, S5, S6, S7, S8) = (10, 3, 3, 16, 12, 12, 2, 2), et une aire totale de 60.
2) (21, 16, 14, 8) est une configuration principale qui donne (70, 8, 21, 99, 48, 63, 6, 21), et une aire totale de 336.
Soit N le nombre de configurations premières principales lorsque AB ≤ 100. Ces N configurations donnent seulement (N - k) aires totales distinctes, car k d'entre elles sont obtenues deux fois. On note P la somme de ces k aires.
Quelle est la valeur de N * P?
Bonjour sanantonio312,
Est-ce que tu as essayé de résoudre le problème des configurations premières d'un rectangle?
Bonjour
Pour avancer un peu, mon programme me donne 415 dispositions pour AB jusqu'à 100. Reste à détailler tout ça.



