Annuler
connectez vous
- Un petit rappel de Cours sur le dénombrement - terminale
- Sept Exercices Q.C.M. sur le dénombrement - terminale
- Complexes, calcul vectoriel, problème - sujet de bac - terminale
- Enseignement scientifique : suite, probabilité, fonction - sujet de bac - terminale
- Enseignement scientifique : suite, probabilité, fonction - sujet de bac - terminale
Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. TerminaleForum de terminale Autres ressourcesTopics traitant de Autres ressources [tout]Lister tous les topics de mathématiques
Niveau terminale
Coniques- Hyperbole
Posté par mbm95
Salut, on sait que dans le repère (o,i,j) (O étant l'un des sommets de l'hyperbole) l'équation de l'hyperbole est:
Son excentricité est donc:
Si on considère H' son image pas la symétrie: y=x
H':
Mon livre de maths dit que l'excentricité de H' est e'=
Je ne comprends pas pourquoi 'a' devient 'b'. C'est aussi le cas pour les équations des directrices etc. : tous les a sont devenus des b après la symétrie, je ne vois pas pourquoi.
Merci d'avance pour votre aide.
bonjour,
si tu intervertis x en y et inversement alors b devient a et a devient b pour que ton equation de depart ne change pas.
Bonjour,
l'excentricité ne change pas par une symétrie !!
c'est une propriété "intrinsèque" de l'hyperbole en question.
ce qui change c'est la façon de la calculer.
à noter que tes prémisses sont déja fausses au départ :
Citation :
on sait que dans le repère (o,i,j) (O étant l'un des sommets de l'hyperbole) l'équation de l'hyperbole est:
on sait que dans le repère (o,i,j) (O étant l'un des sommets de l'hyperbole) l'équation de l'hyperbole est:
c'est faux
O étant au centre de l'hyperbole et pas en un sommet
et en plus l'axe des abscisses étant l'axe focal
sinon l'équation d'une hyperbole dans laquelle l'axe des x est l'axe transverse est
x²/b² - y²/a² = -1
l'excentricté étant toujours sqrt(a²+b²)/a
l'excentricité est le rapport entre la demi distance focale c = sqrt(a²+b²)
et le demi axe focal a
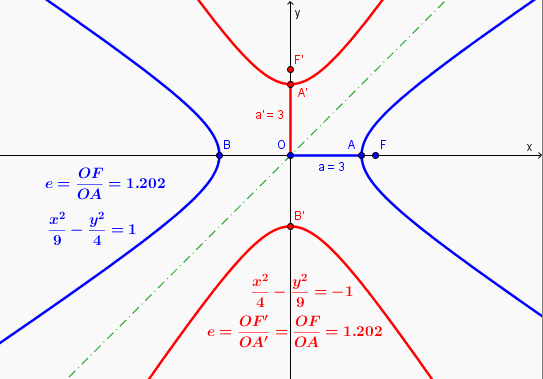
alors oui si on transforme une hyperbole d'axe focal Ox et d'équation x²/a² - y²/b² = 1 par une symétrie / la première bisectrice y=x
on obtient l'hyperbole d'axe transverse ox (et d'axe focal oy)
y²/a² - x²/b² = 1
mais l'excentricité est toujours sqrt(a²+b²)/a
ici sqrt(13)/3 = 1.20185...
évidemment si on rebaptise autrement les a et b on obtient autre chose, mais c'est du pipeau. c'est ça le piège : on a changé la signification de "a" et de "b" !!
au pasage l'excentricité d'une hyperbole est > 1
et celle d'une ellipse < 1
mais l'excentricité est toujours quoi qu'il arrive > 0 (= 0 pour un cercle, = 1 pour une parabole)
@Mathafou donc si on continue à utiliser les mêmes a et b que dans l'hyperbole antécédent (même signification) e est toujours égale à sqrt(a+b)/a ?
Merci pour ta réponse détaillée
PS: Désolé pour l'erreur dans mon énoncé (j'ai appris ce que 'Hyperbole' veut dire aujourd'hui haha)
si on appelle toujours a et b avec la même signification
c'est à dire 2a = distance entre les sommets de l'hyperbole et b "l'autre" oui.
maintenant si on appelle "a" le coefficient dans x²/a² eh bien ça revient à échanger la signification de a et b, donc échanger a et b dans le calcul de l'excentricité.
quant aux valeurs de a et b elles s'échangent aussi de sorte que la valeur de l'excentricité ne change pas.