Inscription / Connexion Nouveau Sujet
Connaître le rayon d'un dodécagone
Bonjour,
J'ai quitté l'école y'a quelques temps et j'aimerais avoir de l'aide sur un petit projet perso (c'est pour faire un plan pour une maquette en papier).
Je voudrais connaitre le rayon d'un dodécagone avec 2 côtés différents.
Un dodécagone régulier a 12 côtés de même longueur.
Pour connaitre son rayon, il suffit de faire :
rayon =
(C = longueur du côté)
Le problème, c'est que moi je veux un dodécagone "régulier" mais ayant 2 longueurs de côté différentes et j'aimerais savoir le rayon.
J'ai fait un schéma pour exposer mon problème
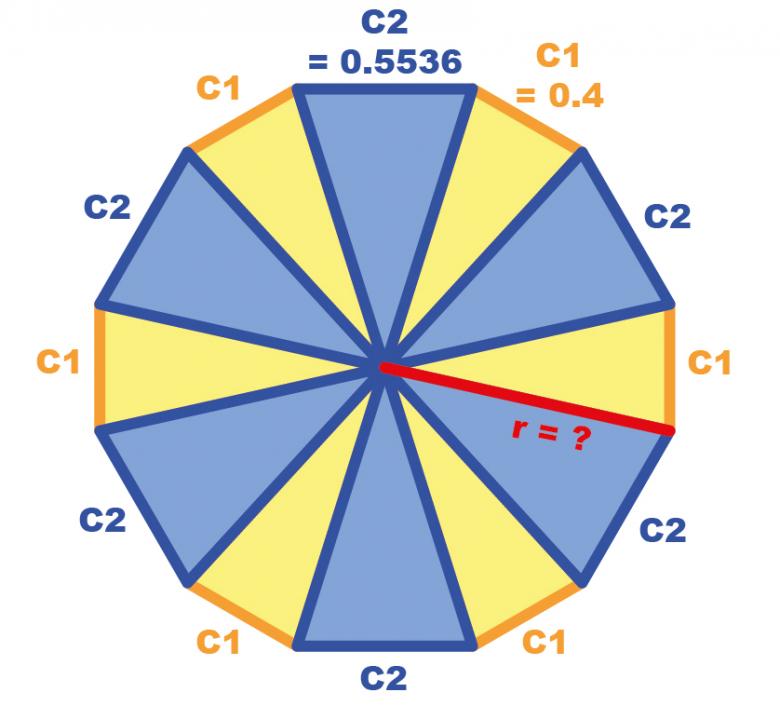
En fait, je voudrais garder C1 (=0.4cm), mais je voudrais que C2 soit égale à 0.5cm.
Quelle est la formule pour connaitre r (le rayon) dans ce cas-là ?
Je connais la formule quand tous les côtés sont identiques (celle que j'ai donnée), mais pas celle que je recherche.
Je coince depuis hier soir.
Merci
Bonjour ,
une formule me parait très difficile à établir .
Par contre , avec des logiciels comme GeoGebra , tu peux trouver la valeur de r très facilement
Bonjour ,
une formule me parait très difficile à établir .
Par contre , avec des logiciels comme GeoGebra , tu peux trouver la valeur de r très facilement
Ah oui, je n'avais pas pensé à GeoGebra. Je testerais ce soir.
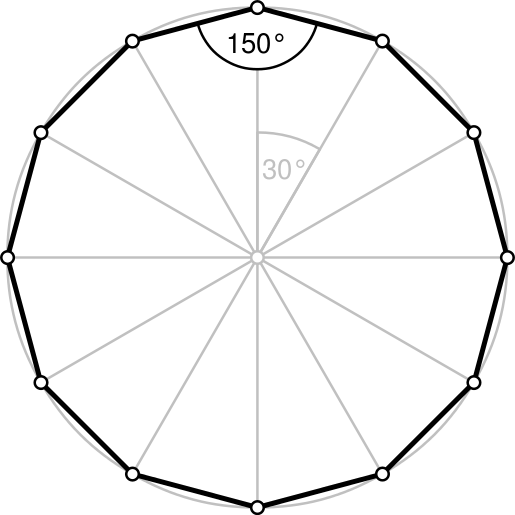
Mais pourquoi as-tu mis un angle de 30 degrés ?
Car 30 degrés est l'angle pour un seul côté dans un dodécagone régulier.
Dans ta figure tu as mis 2 côtés et mon dodécagone n'est pas régulier (enfin je crois. Régulier c'est bien quand tous les côtés sont égaux, non ?).
En tout cas merci d'avoir pris le temps de me répondre 
(dommage qu'on ne puisse pas éditer son message)
Oups, nos messages se sont croisés (je n'avais pas vu les dernières réponses).
Je ne connaissais pas Xcas.
Je regarderais tout ça ce soir, là je n'ai pas le temps.
Mais êtes-vous sûr que c'est 60 degrés ? Car j'ai 2 côtés de longueurs différentes.
L'angle du côté de 0.4cm doit être plus petit que celui dont le côté est de 0.5cm, non ?
En tout cas merci 
bonjour,
construction à la règle et au compas du moment que les côtés sont donnés

tracer deux demi-droites (OI) et (OJ) à 30°, et deux points quelconques avec OI = OJ
construire K avec KI/KJ = 4/5 = AB/BC (ou le rapport des côtes choisi)
c'est à dire IK/IJ = 4/9 = AB/(AB+BC)
la droite (OK) est le lieu des points dont le rapport des distances à (OI) et (OJ) est 4/5
tracer une parallèle à (OI) à la distance 2.5 (la moitié de BC donné)
elle coupe (OK) en le point B
A et C sont les symétriques de B par rapport à (OI) et (OJ)
compléter le dodécagone
Merci énormément pour votre aide !
La formule est bonne !
Dire que j'ai passé presqu'une journée à y réfléchir, à relire mes cours de trigo et que je n'ai pas réussi, et vous, en quelques minutes, vous trouvez la solution !
mathafou : Merci pour les explications.
Je fais mes plans avec Illustrator (logiciel de dessin vectoriel), que j'imprime pour faire mes diverses maquettes en papier. Tracer tout ça à la main me demanderait énormément de temps et ce ne sera pas très précis comparé à l'impression.
Merci encore !
Salut,
J'ai créé mon dodécagone sur mon logiciel (Illustrator), grâce à votre formule pour le rayon.
Mais il me trouve un côté à 0.4001cm (et l'autre à 0.5 comme prévu).
Je précise qu'il ne prends en compte que 4 chiffres après la virgule.
Donc au-lieu de prendre le rayon à 0.869718438067 cm, il me prends 0.8697.
Est-ce à cause de l'arrondi qu'il me donne un côté à 0.4001 ?
Certes, pour mon plan, le 0.001 est insignifiant et totalement négligeable, mais quand même ^^
Y a-t-il moyen d'avoir 0.4 et 0.5 pile poil avec l'arrondi du rayon ?
Ou c'est totalement impossible ?
C'est bizarre , en prenant le même rayon (0.8697) et 0.5 , GeoGebra me donne 0.399980795
Là l'erreur s'explique bien par l'approximation faite sur le rayon .
Ah effectivement, bizarre.
J'ai réessayé plusieurs fois, il me donne parfois des résultats légèrement différents.
Des fois c'est 0.4001, une autre fois c'est bien 0.4 mais l'autre côté est à 0.4999 (au-lieu de 0.5)...
Je me demande si ce n'est pas moi qui construit mal la figure mais je ne pense pas :

Des arrondis seront toujours des arrondis et des calculs approchés toujours des calculs approchés.
et si on enchaine des calculs (conversions en binaire interne, intersections de cercles etc) les erreurs d'arrondis se cumulent
et en gros si l'entrée est à 10-4 près, les calculs et donc les résultats seront au final avec une précision moins bonne que 10-4
et il est impossible de savoir de combien et dans quel sens vu qu'on ne sait pas quels calculs il fait en interne !
même 0.4 est une valeur approchée dans la machine puisque 0.4 décimal s'écrit en binaire 0.011001100110011... avec un nombre infini de chiffres binaires.
que donnerait ma construction géométrique (pour laquelle les seules approximations sont celles de la précision de calcul interne) ?
mais je ne connais pas les possibilités de Illustrator
ceci dit :
Certes, pour mon plan, le 0.001 est insignifiant et totalement négligeable
et faut peut être pas se prendre la tête pour rien...
La construction que tu montres devrait donner 0.4 exactement puisque c'est le rayon que tu utilises . Je ne vois pas comment tu mesures autre chose .
ma construction est rigoureusement exacte (lire) à 10-15 près (la précision de Geogebra) et "mathématiquement" rigoureusement exacte tout court.
à partir des valeurs de 4 et 5 (ou de 0.4 et 0.5) elle donne le rayon du cercle circonscrit
je ne le définis pas à priori comme vous, ni par une valeur calculée, ni par une équation, il est le résultat de la construction même.
(oui, bien sur à l'intérieur il y a des calculs, mais pas du tout ceux de l'équation avec les arcs sinus : des intersections de droites et de cercles uniquement)
si je zoome sur mon point B il est exact "par construction"
(au zoom quasiment maxi de Geogebra)
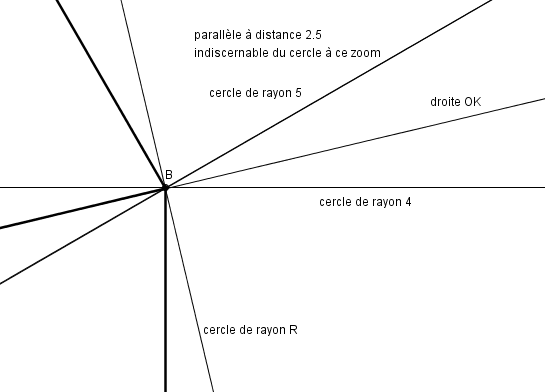
aucun cercle "de rayon 0.8697 etc"
vu que ce cercle est défini à partir de B et pas à partir de son rayon, il passe forcément par B ...
B est défini par l'intersection de deux droites.
les cercles de rayon 4 et 5 sont ici définis par leur rayons et leurs centres
il passent bien par B
normal pour celui de rayon 5 puisque c'est par la parallèle à distance 2.5 que B est défini, mais celui de rayon 4, lui, est indépendant
solve((1-1/(16*R^2))*(1-1/(25*R^2))=(sqrt(3)/2+1/(20*R^2))^2,R)
la solution positive est (sqrt(sqrt(3)*20+41))/10
ce qui montre d'ailleurs la constructibilité à la règle et au compas de ce nombre, ici obtenu en valeur exacte et pas par une solution approchée d'équation avec des arcs sinus ...
(ceci dit les sommes d'arcs sinus ou d'inverses d'arc sinus se ramènent à cette équation si on trafique un peu les formules d'addition trigo)
Re-salut,
En construisant en suivant les instructions de mathafou, j'obtiens effectivement le dodécagone avec des côtés de 0.4 et 0.5 pile poil !
C'est bizarre car les 2 dodécagones (celui construit à "ma" méthode et celui construit grâce à mathafou) ont le même rayon.
Merci beaucoup !
Ceci dit ma méthode est inutilement compliquée :
je m'étais stupidement laissé entrainer par un problème semblable mais inversé : on connaissait le rayon et le rapport des côtés, leur mesure étant inconnue.
bien évidemment la construction simple et directe est :
on trace un angle de 30° et les parallèles à distances 2.5 et 2 qui se coupent en B, la suite idem.

quant aux bizarreries des arrondis de Illustrator, comme déja dit l'incertitude dépend de ses calculs internes et de la façon dont il les enchaine ...
Bonjour,
on trace un angle de 30° et les parallèles à distances 2.5 et 2 qui se coupent en B
qui donne

Bonjour,
sans les vérifications d'usage
Avec
On a tous les droits

Je vois que vous vous amusez bien en donnant des exercices 
lake, tu peux m'expliquer ta formule ? Comment t'as réussi à la trouver ? Apparemment tu t'es basé sur l'explication de traçage du dodécagone puisque tu en as cité un bout.
En effet, je pose la question car j'ai d'autres problèmes identiques mais non pas avec un dodécagone (12 côtés), mais avec des figures de 6, 8, 10, 14 et 16 côtés (désolé, je ne connais pas par cœur le nom de toutes ces figures).
Toujours avec a = 0.4 et b = 0.5 et je cherche le rayon de ces figures.
Si tu peux m'expliquer quand tu l'as trouvé simplement (je suis loin d'avoir votre niveau en maths), comme ça j'essaierai de trouver les formules moi-même sans vous déranger.
Oups, petite erreur dans mon poste précédent (dernière phrase) :
Si tu peux m'expliquer COMMENT tu l'as trouvé simplement (je suis loin d'avoir votre niveau en maths), comme ça j'essaierai de trouver les formules moi-même sans vous déranger.
C'est vraiment dommage qu'on ne puisse pas éditer ses messages, ne serait-ce que pour corriger des fautes.
Bonjour Euline,
Je n'ai fait que tirer les marrons du feu: tout avait été dit par les différents intervenants.

On a donc
d'où l'équation:

Pour tout dire, dès le début de ton topic, j' avais commencé ce genre de calcul mais j'avais eu la très mauvaise idée de partir avec
Les calculs ne se passaient pas très bien; j'avais abandonné... 
Avec les mêmes méthodes, tu peux obtenir une formule analogue fonction des mesures des côtés et
et du nombre total de côtés
:

remarquer que ma construction (la dernière avec juste les deux parallèles) fonctionne quel que soit le nombre pair 2m de côtés
en partant d'un angle pi/m au lieu de pi/6, pour 2m = 12)



