Bonjour,
Fin août, un chercheur à créé un algorithme simulant le mouvement d'un chien de berger.
On trouve facilement des articles le relatant, mais il n'y à pas beaucoup de précisions sur cette algorithme...

A moins d'apprécier traduire l'anglais...

Bonjour,

Je pense que la solution tourne autour de cela:

Un troupeau est au départ considéré comme une forme
plus ou moins elliptique.

L'œil du chien est le sommet d'un angle dont
les deux cotés sont tangents à cette ellipse .

Le chien surveille ces tangentes (contraste entre
la couleur dominante du troupeau et le vert du
pâturage)...

Dès qu'un animal franchit une de ces lignes virtuelles.
le chien se précipite pour la faire rentrer dans le troupeau
puis reviens à l'arrière pour continuer ce manège.

Moi y'en a pas comprendre la question ni la réponse in the Shakespeare language

Imod

--> Imod :

Un p'tiut copier-coller dans reverso (déjà évoqué dans le coin) donne toute la lumière :

je comprends encore moins quand c'est dans la langue Molière , c'est grave docteur

Imod

Bon,


La langue de Molière me sied.

Une ébauche de l'algorithme pourrait être:
1) les brebis sont-elles toutes arrivées à destination? oui=fin
2)non,sont-elles rassemblées ? non, les rassembler
                                  oui, les pousser

Retour au 1)



Alain

Effectivement, c'est un bon début, mais je pense que le problème est légèrement plus complexe que ça...

Pour ceux qui veulent en savoir plus, mais qui ont la flemme de traduire l'anglais, voilà un exposé de ce que j'ai compris de l'exposé (Je ne prétend pas avoir tout compris, si il y a des erreurs, signalez les...):

Concernant la modélisation du mouvement des moutons:

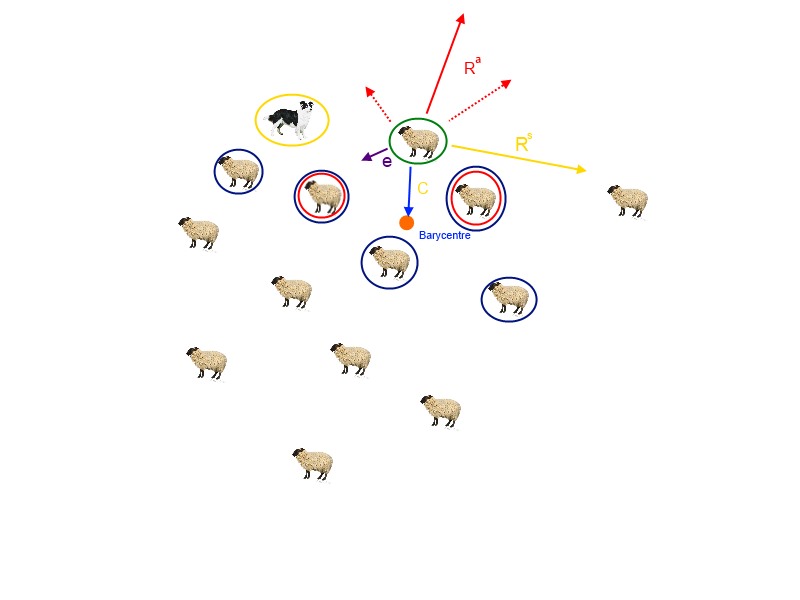
Considérons l'un des moutons... (en vert sur le schéma)
Le mouton a son espace vital, et il s'éloigne donc un peu des moutons qui voudrait trop s'approcher de lui...
Une partie de son mouvement sera donc représentée par un vecteur R^a, qui part en direction opposée des moutons situé à une distance inférieure à r_a.
(sur le schéma, les moutons très proche sont en rouge, R^a est en rouge)

Le mouton à toutefois envie de jouer avec ses copains, et décide de se rapprocher du centre de l'action...
Une partie de son mouvement est donc dirigée vers le barycentre des n plus proches voisins, représentée par un vecteur C.
(sur le schéma, n = 5, ces 5 moutons sont en bleu, le barycentre est orange, C est bleu)

Le mouton à évidemment peur du chien de berger , et cherche à s'en éloigner...
Une partie de son mouvement sera donc représentée par un vecteur R^s, en direction opposée à celle du chien.
(Sur le schéma, le chien est en jaune , R^s est en jaune)

Si le mouton est situé à une distance du chien de berger supérieure à r_s, le mouton ne voit pas le chien, le vecteur R^ssera donc nul.

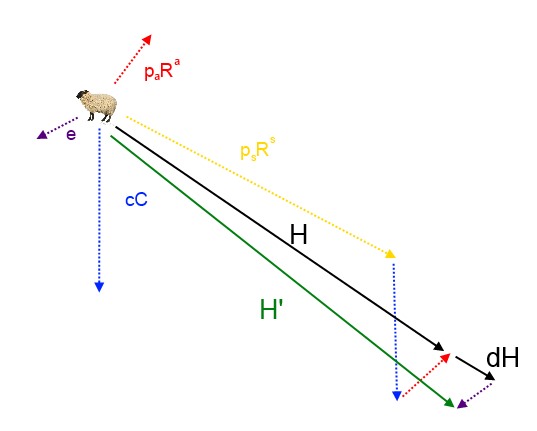
Le mouton va évidemment effectuer ces 3 déplacements en même temps, déplacement modélisé par la somme vectorielle H = PaR^a + cC + PsR^s, avec Pa, c et Ps des coefficients dépendant du modèle, traduisant l'importance de chaque déplacement. (voir 2eme schéma, H en noir...)

Ainsi, R^a ne présentera pas beaucoup d'importance par rapport à R^s et c.

De plus, le mouton a des problèmes de freinage...
On ajoute donc un faible terme d'inertie dH, prolongeant la trajectoire de H.

Enfin, les moutons n'étant pas des machines, ils ont certains mouvements imprévisibles, qui seront modélisés par l'ajout d'un vecteur aléatoire de faible norme, e (en violet sur le schéma...)

On obtient alors le vecteur déplacement du mouton: H' (en vert sur le schéma 2)



La suite pour le déplacement du chien, bref, ce qui nous intéresse...

2eme épisode:

Le déplacement du chien:
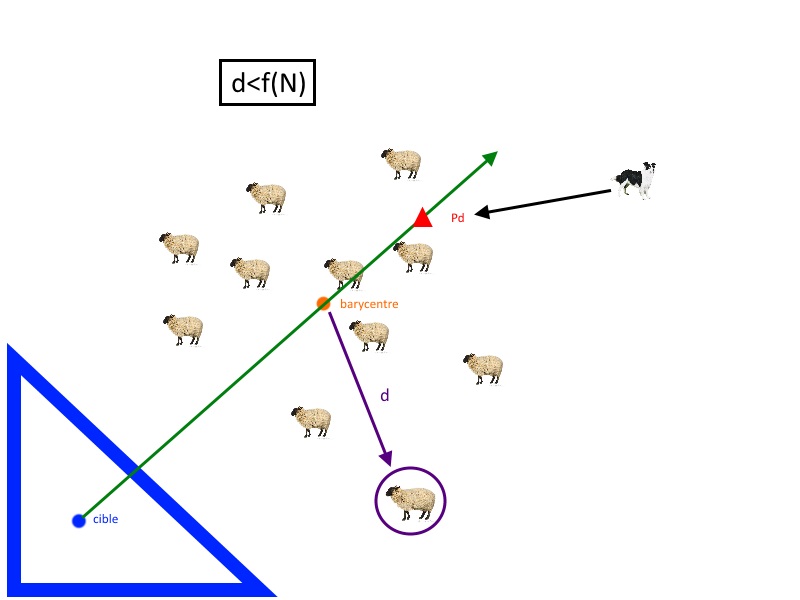
Le rôle du chien est de déplacer les moutons dans le coin inférieur gauche.(noté cible sur le schéma, en bleu...)

Si le chien est situé à une distance de moins de 3r_a (r_a étant la distance caractérisant les moutons gênant, car trop près...), alors il ne se déplace pas.

Sinon, notons d la distance du barycentre de l'ensemble des moutons au plus éloigné de ces moutons (en violet sur le schéma)
Considérons aussi le nombre f(N), (dépendant du nombre N de moutons).

si d<f(N):

Le chien est dit en phase de "conduite"...
Considérons la droite portée par la cible, et le barycentre des moutons(en vert sur le schéma...)
On y place un point Pd, situé légèrement au delà du barycentre.
Le mouvement du chien sera donc dirigé vers ce point.
Il se déplacera d'une distance delta dans cette direction.



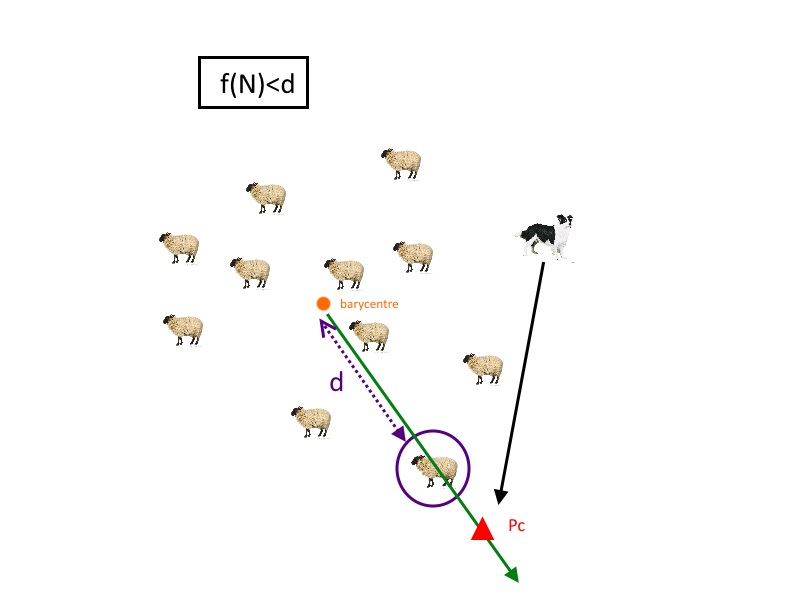
si f(N)<d:
Le chien est dit en phase de "collecte"...
Considérons la droite portée par le barycentre et le mouton le plus éloigné du barycentre.
On y place un point Pc situé légèrement au delà du mouton.
Le mouvement du chien sera donc dirigé vers ce point.
Il se déplacera d'une distance delta dans cette direction.



Si j'ai le courage, un dernier post sur les conclusions quand au réalisme de cette simulation.
En attendant, vous pouvez juger vous même du résultat en regardant les simulations effectuées...


Le texte en anglais est finalement plutôt accessible.
La solution est assez différente de l'hypothèse des tangentes de dpi...

Bonjour  weierstrass,


Je reconnais le gros travail que tu as accompli,nous avons sous
les yeux une simulation expliquée et claire.

Mon objectif était un peu différent,je pensais à un modèle applicable
à une organisation humaine telle que le pilotage d'un projet d'entreprise,
d'autres questions alors se posent;qu'est-ce que la "distance" entre acteurs?
leur degré d'assimilation au temps t,leur enthousiasme ; comment les mesurer?



Alain