La somme des numéros de deux voisins est égale à ceux des personnes diamétralement opposés (nous dirons en face pour simplifier). Pour une personne cela est vrai avec le voisin de gauche comme avec le voisin de droite, ce qui entraîne que la différence de numéros avec celui d'en face est la même pour le voisin de droite et celui de gauche, donc que ces différences sont les mêmes de deux en deux, et comme il y a un nombre impair de diamètres, que ces différences sont les mêmes sur chaque diamètre, au signe près, avec altermance de différences positives et négatives.
Ces différences ne peuvent donc être égales qu'à 15; le numéro 16 est toujours assis face au 1, et les numéros 2 à 15 sont chacun sur un des 14 diamètres restant, en respectant l'alternance des signes. Il y a donc 14! configurations possibles soit 87178291200. Au rythme de 3 repas par jour, 52 semaines de 7 jours par an , cela fait 79833600 ans avant d'épuiser toutes les configurations.
400 ans se sont déjà écoulés, donc il reste 79833200 ans, ... avant la fin du monde, ce qui devrait me permettre de résoudre encore quelques petites énigmes

bonjour,

D'après une interprétation plus que personnelle des différents cas à 6 mathématiciens (mathématiciens moines, ce qui est plutot rare), j'en déduis que le nombre de possibilités est de 2x14! (a ne pas lire 2x14 oh je suis étoné! mais 2x14 factoriel)

ainsi, si je divise mon résultat par le nombre de repas pris dans une année et si j'ote les 400 premières années, il restera exactement 159666800 ans avant la fin du monde.

Ca sent le poisson tout ça, mais bon...

Merci

Bonjour,

Voici ma proposition :

La clé de l'énigme réside dans la façon dont on arrive à placer les 30 mathématiciens.

Cherchons à en placer 1 sur 2, depuis le n°1 et dans le sens des aiguilles d'une montre. Nous avons donc une série de 15 personnes à placer. L'autre série de 15 personnes se déduit de la première de la façon suivante : avec un décalage d'un demi-tour de la table, la deuxième série de 15 suit l'évolution des nombres de la première avec un écart constant. En effet, prenons un nombre au hasard, A, et ses deux suivants : B et C. On voit que (A+B) - (B+C) = A - C est égal à la différence des 2 nombres en face de A et C, puisque A+B et B+C sont égaux aux sommes des nombres qui sont en face de la table.

Je traduits : si la première série (toujours une personne sur 2 du plan de table) commence par 1, 9, 2, 4…, la seconde série, avec un écart de 6, commence par 7, 15, 8, 10….

Il suffit donc que l'on compose les deux séries, avec un écart constant, sans qu'un même nombre se retrouve dans les 2 séries.

Composons les séries : les seules possibles sont :
Avec un écart de 1, les 2 séries sont (chaque série est ordonnée du plus petit au plus grand):
1 3 5 7 9 11 13 15 17 19 21 23 25 27 29
2 4 6 8 10 12 14 16 18 20 22 24 26 28 30

Avec un écart de 3, les 2 séries sont :
1 2 3 7 8 9 13 14 15 19 20 21 25 26 27
4 5 6 10 11 12 16 17 18 22 23 24 28 29 30

Avec un écart de 5, les deux séries sont :
1 2 3 4 5 11 12 13 14 15 21 22 23 24 25
6 7 8 9 10 16 17 18 19 20 26 27 28 29 30

Avec un écart de 15, les deux séries sont :
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
16 17 18 19 20 21 22 23 24 25 26 27 28 29 30

Pour maintenant évaluer le nombre de plans de table possibles, on sait que lorsqu'on prend une série (la première du couple de série), la place du 1 est fixe. Les autres sont placés (une place sur 2 donc) de façon aléatoire. Il y a donc : 14 ! solutions (14 factorielle). La seconde série de 15 est placée automatiquement sans marge de manœuvre possible. Comme il y a 4 couples de séries, il y a :
4 x 14 ! plans de table possible.

A 3 x 7 x 52 repas par an, le nombre d'années est égal à :
4 x 14 ! / (3 x 7 x 13 x 4) = 8 x 11 ! = 319 334 400

400 années se sont écoulées : il reste encore 319 334 000 années précisément (au repas près ! ) avant la fin du concile et avant la fin du monde. Ca va, Minkus pourra encore nous proposer d'ici là quelques énigmes (à près de 1 tous les 2 jours, on a le temps d'en voir …)

Voici juste un petit exemple de plan de table (à lire dans le sens des aiguilles d'one montre, et dans l'autre sens pour un deuxième exemple), fait à partir d'un couple de séries distantes de 3 :
1 30 7 12 14 24 15 6 2 11 26 22 25 23 13 4 27 10 9 17 21 18 3 5 8 29 19 28 20 16
Le chiffre 1 et, à son opposé, le 4 sont les premiers nombres des 2 séries. La première série est donc : 1 7 14 15 etc… et la seconde : 4 10 17 18

Deux petites remarques sur l'énoncé : que font les moines dans cette affaire, à la fin de l'énoncé ? Je croyais qu'il s'agissait de mathématiciens. Mais il est vrai que certains moines sont (ou ont été) d'illustres mathématiciens ou autres scientifiques. Par ailleurs, j'ai considéré comme une coquille de l'énoncé la mention : « à chaque repas la disposition globale doit être différente de celle obtenue à un repas quelconque depuis 400 ans. ». Il me semble qu'il est plus judicieux de dire : « depuis l'origine du concile », car sinon le concile est éternel ! Il y a en effet plus de plan de table que nécessaire, pour ne pas en avoir un identique dans les 400 jours qui précèdent !


Donc ma réponse à cette énigme est : 319 334 000 années précisément, à moins que ce ne soit une question d'éternité (voir remarque ci-dessus…)

Merci pour cette magnifique énigme !

BONJOUR
Ma réponse est un peut exagérée mais pour la fin du monde ça pourrait être possible, donc ou ça passe ou ça casse: le nombres d'années réstantes est 1197503600.

                   LOTFI

Bonsoir, je ne prévoyais pas de faire celle-là, mais il faut bien que je rattrape mon poisson de l'énigme à une étoile : tête bêche  

Pendant combien d'années existera encore le concile ? réponse 319 334 000 années.

^{With a little help from my friends}

Le concile existera encore pendant 239500400 années : (14!*3/1092)-400 (en simplifiant : (12!/2)-400) (il y aura peut-être des catastrophes telles qu'une glaciation sévère, une pluie intensive de météorite, un déréglement causé par l'approche de la lune,...)

En partant de 1 dans un sens, on trouve les nombres A, B, ..., N, O; en continuant on trouve A+1-O, B-1+O, etc jusqu'à N avec x+1-O ou x-1+O selon que x a un rang impair ou pair dans l'alphabet.
On en conclut que les nombres sont toujours regroupés en deux groupes : les 'petits', à distance paire de '1' et leurs opposés respectifs, les 'grands'. Un 'grand' est le 'petit' opposé + O - 1.
Les premiers 'grands' sont les O-1 plus grands nombres (aucun 'petit' ne peut atteindre ce plafond). Les premiers 'petits' nombres sont les O-1 premiers 'grands' diminués de O-1.
Les seconds 'grands' sont les 0-1 plus grands nombres parmi les restants et ainsi de suite. Il y a une alternance descendante de 0-1 'grands' et de 0-1 'petits'.
D'autre part, il y a quatorze groupes d'un nombre et de son opposé. Ces groupes ont la même différence. Leur somme totale est donc paire. Comme les nombres de 1 à 30 ont pour somme 465, O est pair.
Une fois les 'grands' déterminés, on peut les répartir librement sur les places à distance impaire de '1', hormis la place de O. Chaque 'petit' aura alors une place unique, à l'opposé de son 'grand' correspondant. Il y a autant de fois 14! combinaisons que de O possibles.
O = 2 : 'grands' = {30, 28, 26, ..., 4}; petits = {29, 27, 25, ..., 3}
O = 4 : 'grands' = {30, 29, 28, 24, 23, 22, 18, 17, 16, 12, 11, 10, 6, 5}; 'petits' = {27, 26, 25, 21, 20, 19, 15, 14, 13, 9, 8, 7, 3, 2}
O = 6 : 'grands' = {30, 29, 28, 27, 26, 20, 19, 18, 17, 16, 10, 9, 8, 7}; 'petits' = {25, 24, 23, 22, 21, 15, 14, 13, 12, 11, 5, 4, 3, 2}
O = 8 : on a des 'grands' de 30 à 24 et des 'petits' de 23 à 17; puis des 'grands' de 16 à 10; mais alors O interfère avec le 'petit' 8.
O = 10 : on a des 'grands' de 30 à 22 et des 'petits' de 21 à 12; il ne reste plus assez de nombres pour un nouveau couple de neuvaines.
O = 12 ou 14 : O interférerait avec un 'petit'.
O >=16 : il y aurait au moins 15 'grands' et 15 'petits', ce qui est impossible puisqu'ils sont 28 en tout.
Donc il y a trois O possibles (2, 4, 6) et 14!*3 combinaisons.

Bonjour,

J'ai généralisé a partir de simulations sur 2, 4, 6, 8 ou 10 membres du concile.

Pour que la configuration requise soit possible, il faut un nombre pair de membres.
De plus ce nombre doit être de la forme 4k+2 (il n'y a pas de solution pour 4 ou 8 membres).
Avec 2 membres: 1 possibilité
Avec 6 membres: 4 possibilités
Avec 10 membres: 48 possibilités

Je conjecture, pour n membres, n>2, que le nombre de configurations différentes est 2*((n/2)-1)!.

Ce qui nous donne, pour n=30, 2*14! soit 174356582400 configurations.
Le concile existera donc encore pendant (174356582400-436800)/(3*364) = 159666800 ans, soit 1596668 siécles.

De plus toutes ces configurations se divisent en deux catégories:
1) Chaque membre a un écart de 15 avec son vis-à-vis.
2) Chaque membre n pair a pour vis-à-vis n-1, et chaque membre impair n+1.
Chacun n'aura donc en face de lui que toujours les deux mêmes têtes!

Enigme vraiment passionnante. Merci, minkus.
(en éspérant ne pas avoir été trop vite en besogne...)

A+,
gloubi

Bonsoir ! Je me lance pour ce 32eme défi...

Le concile des Trentes a encore 319334000 années d'existence devant lui ! (= 4x14!/(3x7x52) - 400)

Je suppose que les mathématiciens choisissent des numéros distincts pour se reconnaître. Egalement, je suppose qu'ils ont cherché à choisir les nombres de sorte à ce que le concile dure le plus longtemps possible ! Il n'est pas explicite dans l'énoncé que les identifiants des membres du concile sont les entiers de 1 à 30, et même si au final la solution que je propose est celle-là, j'ai abordé le problème dans le sens le plus large : les numéros des mathématiciens forment un ensemble de 32 entiers positifs, incluant 1.

L'image 1 ci-dessous montre le cas général pour la répartition des membres du concile dans le cas où ils ne seraient que 10 (histoire de simplifier...) : les entiers N, a, b, c et d permettent de décrire sans ambiguïté n'importe quelle configuration de numéros + emplacements respectant les conditions de l'énoncé. Pour N donné, on a deux places "fixes" : celle du numéro 1, et celle du N+1 en face. Par contre, toutes les permutations de a, b, c et d sont acceptables, il y a donc 4! dispositions possibles pour une valeur de N fixée.

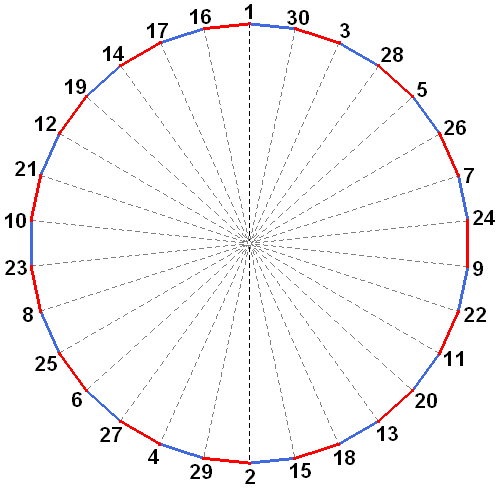
Dans un concile à trente, on aura pour N donné, 14! configurations possibles. Le problème est alors le suivant : les mathématiciens ayant fait leur choix de numéros, est-il possible que plusieurs d'entre eux puissent prendre place face au numéro 1 ? Autrement dit, existe-t-il des ensembles de numéros qui autorisent à avoir le choix entre plusieurs valeurs pour l'entier N ? Chaque valeur supplémentaire multiplie en effet le nombre total de configurations, ce qui est important pour la survie du concile ! Il se trouve que si les mathématiciens choisissent les entiers de 1 à 30, il y a 4 valeurs possibles de N (1, 3, 5 et 15, qui sont les diviseurs de 30/2, voir seconde image). Cela donne 4x14! configurations possibles, d'où le résultat donné plus haut.  

Je ne suis pas entiérement satisfait de ma réponse car je n'ai pas la preuve qu'aucune autre configuration d'entiers n'autoriserait un plus grand nombre de choix possibles pour N ! Intuitivement je dirais que non ! Mais...

Merci en tout cas pour ce défi... au temps !

Figure 1: Cas général pour un concile à 10. N peut valoir 1 ou 5.


Figure 2: 4 valeurs possibles de N pour le concile des 30. Partant d'une case verte on arrive sur une case jaune en ajoutant N.

Bonsoir,

une énigme qui mérite bien ses 4 étoiles !

En notant les 30 places et en posant (la place réservée du G.O.), on a les 15 équations suivantes:

et
Par sommation de ces 15 équations, on obtient:
, i.e. les sommes de gauche et droite sont égales.
Or , d'où .
Par ailleurs, pour que les sommes soient égales, il faut pouvoir interchanger (pour compensation) de façon continue des nombres entre ces deux sommes, ce qui n'est possible que si ou   (plus généralement, si n est tel que est impair i.e. n=2(2m+1), ).
Il en résulte que ou , chacune de ces deux possibilités produisant un nombre égal de solutions
(quitte à poser ).
Ainsi, on a et .
Ensuite, on choisit ce qui impose forcément .
Puis le choix qui induit ,... etc. (voir figure).
Il faut ainsi choisir 14 nombres distincts donnant lieu à des sommes compatibles avec tel que les soient également tous distincts et de somme S, soit 14! possibilités (plus généralement ) (et en comptant les solutions symétriques par rapport à l'axe )
Le dénombrement final donne donc dispositions possibles (plus généralement ).

Reste enfin à calculer le nombre d'années restantes.
Les 400 premières années ont usé possibilités.
Il reste donc exactement la bagatelle de années.  (ou 174356145600 possibilités)

La fin du monde n'est pas imminente !
Longue vie au "conseil des sages" qui sont a priori des mathématiciens ...

En bonus, certainement la première disposition (il y a 400 ans),
car la plus triviale :

Bonne nuit

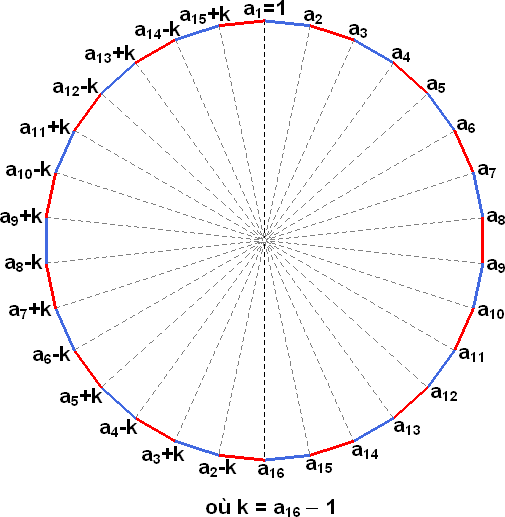
Soit et 2 couples l'un en face de l'autre dans une solution. On a et donc :

Alors la différence entre 2 nombres l'un en face de l'autre est constante (lors d'un même repas), au signe près. On remarque qu'il suffit que tous les soient égaux entre eux et égaux à tous les , pour que la configuration soit acceptable.
Par exemple, si on prend pour différence 1, on peut avoir une solution basée sur les couples (1,2) (3,4) (5,6) (7,8) ... ce qui donne en parcourant la table :
1 4 5 8 .... (en face de 1) 2 3 6 7 ....
On peut changer l'ordre des couples de base (sauf le couple qui contient 1) : ce qui fait 14! (14 = 15 couples -1) possibilités de configurations autour de la table à partir des couples (1,2) (3,4) (5,6) ...
Il reste à savoir combien d'ensembles de couples on peut former : en réfléchissant sur des petites valeurs, on se rend compte qu'il y en a (où est le nombre de diviseurs de incluant et ) soit ici qui vaut 4.
Il y a donc configurations totales possibles, soit 348 712 728 000 configurations restantes : le concile existera donc encore pendant 319 334 000 ans

La formule générale du nombre de configurations possibles est : Il faut également que soit pair (sinon qui est la personne diamétralement opposée ?) et que soit impair (sinon, il n'y a pas de solution)

UN GRAND MERCI POUR CETTE ENIGME GENIALE !
Sans informatique, l'énigme est plus chic (en reprenant un slogan bien connu contre l'alcool)

Pas facile, celle-la !!!
L'informatique est impuissante tant le temps de calcul est important. La récurrence ne marche pas ; en tout cas je n'ai rien trouvé !!
Reste  la logique.
Si je fixe le nombre qui fait face au n°1 et qui donne avec 1 une différence de X, je m'aperçois que, si je peux énumérer tous les chiffres de 1 à 30, la différence entre deux nombres qui se font face est successivement -X, +X, -X, +X…+X (15-1=14 fois).
Ayant placé le doublet contenant le 1, j'ai 14 manières de placer le second doublet, puis 13 manières de placer le troisième doublet, soit 14! manières de placer mes doublets.
Mais alors, combien de valeurs de X conviennent, c'est-à-dire permettant d'intégrer tous le nombres de 1 à 30 dans des doublets, sans aucune répétition ?
Ces doublets peuvent se regrouper en « groupes de doublets ».
Pour une différence de X, le premier groupe de doublets est constitué par les X doublets suivants : (1, X+1) ; (2, X+2) ; (3, X+3) ;…..(X, 2X).
Les groupes de doublets suivants sont constitués de X doublets, chacun décalé de 2X, puis de 4X, puis de 6X, etc… par rapport aux doublets du premier groupe.
Le nombre total de mathématiciens doit donc être un multiple de 2X.
Pour 30 mathématiciens, seul X=1, X=3, X=5 et X=15 conviennent. Pour chacune de ces différences, le nombre de possibilités est 14!.
Le nombre total de répartitions possibles est donc 4*14! (ouf !!!), soit 4*14! repas à prendre avec des dispositions différentes, chacune respectant les contraintes de l'énoncé.

En considérant 3 repas par jour, 7 jours par semaine, et 52 semaines par an, le nombre d'années à prendre des repas est égal à (4*14!)/(3*7*52) = 319 334 400 ans.
Comme 400 ans se sont déjà passés, il reste au Concile des Trentes encore 319 334 000 années d'existence….soit un sacré bail.

Merci pour cette très très belle énigme !!!

Bonjour Minkus,

Dur,dur,dur.

Sauf erreur de raisonnement!
Le concile existera encore pendant années (2.14!/3/7/52 -400)
Il fallait que je trouve les termes suivants de la suite:
2.2!,2.4!,2.6!,3.8!,2.10!,x,y

re,
Cela ne change peut-être pas grand chose
mais j'ai sûrement oublié un 6 dans la bataille.
La bonne réponse est 159 666 800

Bonjour
Ca devrait être 2*14!/(3.7.52) - 400
soit années
A+

Le concile existera encore pendant 1.3809277858434684253090215332106e+710 années... Mais, il doit sans doute y avoir un tit noeud qque part...

Bonjour,

Je tente le coup de poker sans grandes convictions...

Je pense que le nombre de mathématiciens autour de la table n'est pas choisi au hasard.

Je me demande si la base n'est pas une suite de Fibonacci 1, 3, 7, 15, ....
obtenue bien-sûr à partir de n = 1, 2, 3, 4, ....
qui donnerait un nombre de places autour de la table de 2, 6, 14, 30, ....
pour lequel il y a des solutions respectivement de 1, 4, 1440, et... celle-là, je ne l'ai pas trouvée, hélas !!

Le nombre de solutions pourrait être 2.(2ⁿ-2)! ce qui donnerait pour n=4 (30 places) un nombre de 174 356 852 400 solutions.

En déduisant les 436 800 d'jà utilisées, il en reste 174 356 145 600 à raison de 1 092 repas par an donc :

Le concile existera encore pendant soit un peu moins de 160 millions d'années

Les premiers hommes sont apparus il y a 6 millions d'années et l'âge de la terre est de 5 Milliards d'années. Elle a encore, devant elle, 5 Milliard d'années avant d'être aspirée par le soleil mourrant. Ma réponse, même fausse, est possible donc je signe (peut-être pour une arête...)!!

Merci et à bientôt, KiKo21.

le concile pourra encore se tenir pendant 319 334 000 années

Bonjour à tous.

Si on considère le nombre de participations, le nombre de bonnes réponses (Bravo à Savoie, Bornéo, Torpedo, nobody, Nofotur2 et Evariste) et les commentaires, il semble bien que ce défi soit le plus difficile de tous ceux que je vous ai proposés à ce jour. C'est pour cette raison que je l'ai laissé ouvert plus longtemps qu'à l'habitude.

Aussi vous en proposé-je une correction détaillée.

Tout d'abord, il s'agit de trouver les différentes dispositions possibles avant d'en dénombrer le nombre. Si on appelle A et B deux voisins et A' et B' ceux qui leur font face, on doit alors avoir A + B = A' + B' ce qui implique A - A' = B - B'. Ainsi la différence entre les numéros de deux mathématiciens diamètralement opposés doit être constante.

Deux dispositions sont obtenues avec un écart de 15 et avec un écart de 1. La première donne la disposition suivante :
1    2   3   4  5   6   7   8   9  10 11 12 13 14 15
16 17 18 19 20 21 22 23 24 25 26 27 28 29 30

La deuxième donne la liste des nombres pairs couplés avec les impairs.

1 3 5 7  9  11 13 15 17 19 21 23 25 27 29
2 4 6 8 10 12 14 16 18 20 22 24 26 28 30

Mais il y a deux autres dispositionspossibles avec des écarts de 3 et 5.

1 2 3   7   8   9 13 14 15 19 20 21 25 26 27
4 5 6 10 11 12 16 17 18 22 23 24 28 29 30

1 2 3 4  5  11 12 13 14 15 21 22 23 24 25
6 7 8 9 10 16 17 18 19 20 26 27 28 29 30

En fait, on peut démontrer que l'écart K doit être tel que 2K divise 30 ce qui donne bien comme seules valeurs K=1 K=3 K=5 et K=15.

Pour s'en convaincre, il suffit de faire la liste des nombres avec un écart de K.

On a d'abord   1 2 3  .... K qui correspond à 1+K 2+K 3+K ..... 2K. Ensuite on peut continuer avec les nombres de 2K+1 à 4K. Et on doit arriver à 30. Chaque groupe contenant 2K nombres, on a bien 2K qui divise 30.

Maintenant il faut dénombrer les possibilités pour chaque disposition. (Cette partie a été mieux réussie.)
Étant donné que le numéro 1 est placé, on a le choix pour 14 personnes car les 15 restantes sont placés en respectant la disposition. Cela donne donc 14!

En divisant par 3*7*52 dispositions par an on obtient (4*14!)/(3*7*52) = 319 334 400.

En retirant les 400 années déjà écoulées, on trouve 319 334 000 années.

Voilà voilà encore de beaux jours à venir pour le concile

Merci pour votre participation.

mnkus

PS1: La confusion moines/mathématiciens vient de l'adaptation. L'énoncé original parlait de 30 moines de la région de Trente.

PS2: Bornéo, visiblement tu as des amis hauts placés ! Certains feraient-ils partie du concile ? Ou parles-tu encore d'Excel ?

Salut Minkus. J'ai dans mes amis des gens très bons en maths, qui pourraient facilement m'aider quand je n'y arrive vraiment pas. Le problème, c'est que ça les fait sourire... il ne reste donc que les amis virtuels

ça peut paraître bête, mais le fait d'avoir répondu (faux) comme la majorité des gens me rassure quant à ma reflexion...

Je suis donc malgré mon poisson tres content de moi, même si je voyais l'extinction de l'humanité 2 fois trop proche.. (on ne se congratule jamais assez...)

Merci encore pour cette énigme,

Chaudrack le frappeur de tôle