Inscription / Connexion Nouveau Sujet
DEFI 94 : Partition.



Bonjour a tous,
Un peu surbooké, presque une semaine sans énigme !
Bon je poste finalement le défi 4 étoiles promis.
Voilà de quoi il s'agit.
Il s'agit de trouver la plus longue suite de N nombres decimaux strictement compris entre 0 et 1 verifiant les conditions suivantes :
Les 2 premiers doivent être situés chacun dans une moitié différente de l'intervalle ]0;1[. C'est-à-dire que l'un doit être dans l'intervalle ]0;[ et l'autre dans l'intervalle ]
;1[.
Par exemple 0,1 et 0,7 ou 0,7 et 0,1 l'ordre n'important pas.
Pour les 3 premiers on doit en avoir un dans ]0;[, un autre dans ]
;
[ et un autre dans l'intervalle ]
;1[.
Et ainsi de suite pour tout n entre 2 et N,
Les n premiers nombres doivent être répartis de telle facon qu'il n'y en ait qu'un seul dans chaque n-ième intervalle ouvert de l'intervalle ]0;1[, c'est-a-dire un dans ]0;[, un autre dans ]
;
[ etc et un dans ]
;1[
Un exemple de début possible pour être sûr d'avoir été clair : 0,7 0,2 0,4.
Les 2 premiers sont bien chacun dans une moitié différente de l'intervalle ]0;1[.
Les 3 premiers sont bien chacun dans un tiers différent de l'intervalle ]0;1[.
Jusqu'où pourrez-vous aller ?
Autrement dit : quelle est la plus grande valeur de N possible ?
Vous indiquerez la suite obtenue.
minkus
 Bonsoir,
Bonsoir,
bon ben je me lance... mais faut avouer que c'est au moins une 5 étoiles celle-là!
Je n'arrive pas à dépasser 17 (obtenu difficilement d'ailleurs). Je n'ai pas réussi non plus à trouver de raisonnement fixant une limite donc... bref.
Je propose donc une suite de longueur dont voici, dans l'ordre, des éléments possibles (les choix étant infinis!):
0,58 (A)
0,29 (B)
0,99 (C)
0,075 (D)
0,73 (E)
0,46 (F)
0,15 (G)
0,83 (H)
0,38 (I)
0,66 (J)
0,22 (K)
0,89 (L)
0,51 (M)
0,01 (N)
0,79 (O)
0,33 (P)
0,59 (Q)
Rien que vérifier prend un temps fou... bon courage minkus !
Pour trouver, j'ai tatonné à partir du graphique ci-dessous:
17 segments (20 à l'origine, j'étais ambitieux) de même longueur découpés en n parties égales. En bleu figure la solution proposée...
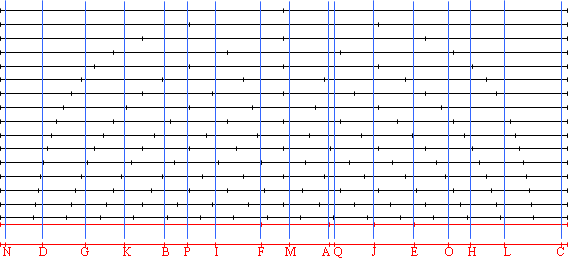
Par ailleurs, j'ai également utilisé excel pour avoir des valeurs précises de chaque intervalle. Ensuite, j'ai bien ramé  (mais bon vu le nombre de réponse, je ne suis certainement pas le seul).
(mais bon vu le nombre de réponse, je ne suis certainement pas le seul).

Voilà. C'est l'heure d'aller au lit.... alea jacta est.
Merci pour l'énigme.




 Bonjour,
Bonjour,
Je ne trouve pas mieux que N = 10 avec une suite qui peut être la suivante, présentée dans l'ordre dans lequel on place les nombres, à savoir :
Le premier est compris entre 0 et 1
Les 2 premiers compris chacun dans les intervalles 0 - ½ - 1
Les 3 premiers compris chacun dans les intervalles 0 - 1/3 - 2/3 - 1
Etc…
0,00001
0,99999
0,50001
0,25001
0,75001
0,37501
0,62501
0,12501
0,87501
0,43751
Merci pour cette énigme.
 bonjour,
bonjour,
je n'ai pas su aller au delà de N=13
voilà une suite possible:
0,06 - 0,95 - 0,48 - 0,695 - 0,225 - 0,56 - 0,848 - 0,368 - 0,13 - 0,78 - 0,28 - 0,64 - 0,4
j'ai fait cela géométriquement en utilisant une droite et en positionnant des segments pour chaque élément à chaque étape vérifiant la condition
je joint mon schéma ci-dessous (j'éspère que je me fais comprendre...)
j'ai été bloqué à l'étape N=14
bon, je ne suis pas convaincu à 100% que l'on ne puisse pas faire mieux, mais avec la méthode que j'ai utilisée, je n'ai pas su faire mieux.

 Après avoir tenté une programmation du problème (j'ai trouvé une solution pour 17, mais mon programme bouclait pendant des heures pour 18), j'avoue humblement m'être tourné vers les ressources du net.
Après avoir tenté une programmation du problème (j'ai trouvé une solution pour 17, mais mon programme bouclait pendant des heures pour 18), j'avoue humblement m'être tourné vers les ressources du net.
Voici ce que j'y ai trouvé :" Ce problème étrange, comme le dit Martin Gardner dans sa rubrique de Pour la Science en novembre 1983, parut pour la première fois dans Cent problèmes élémentaires de mathématiques résolus du mathématicien polonais Hugo Steinhaus. Dans son ouvrage, ce dernier publie une solution pour 14 points et annonce dans une note que M. Warmus a démontré que 17 est la limite".
La valeur maximale possible pour N est donc 17.
Voici une suite décimale solution (3 chiffres après la virgule) :
0,055-0,944-0,421-0,708-0,269-0,542-0,850-0,136-0,619-0,350-0,772-0,210-0,476-0,884-0,069-0,650-0,355.




Après avoir longtemps cherché une réponse "mathématique" à cette énigme, je me suis tourné vers l'informatique. "Mais comment résoudre un problème avec des variables réelles (ou presque) sur un ordinateur" me direz vous : j'en donne une explication après. Après une journée entière de grattage de tête, mon programme me renvoyait une solution pour N=17 et aucune pour N=18. Alors, mais sans entière celconviction, je réponds le N maximum demandé est 17. En revanche, voilà un exemple de suite dont je suis sûr :
0.0294 0.5420 0.8516 0.2697 0.7101 0.4226 0.9258 0.1716 0.6202
0.3431 0.7735 0.0871 0.4853 0.9706 0.2071 0.6569 0.3550
Plusieurs remarques avant d'expliquer mon algorithme :
* Pour fini, peu importe que les nombres cherchés soient décimaux ou juste réels. En effet, en subdivisant
en
segments
de tailles égales, on se rend compte que si
est le
-ème terme solution, et si
alors tout réel du segment
associé peut remplacer
dans la solution.
étant un ouvert non vide, et l'ensemble des décimaux étant dense dans les réels, on pourra toujours trouver déduire d'une solution "réelle" une solution "décimale".
* Ainsi, le premier terme de ma solution est 0.0294 et fait partie de l'intervalle de Farey : donc il peut être remplacé par n'importe quel terme de cet intervalle. A l'ordre 17 qui est je l'espère l'ordre maximum, le nombre de suites solutions est infini (et dénombrable je pense).
Mon algorithme :
* Avec ma première remarque, j'ai rendu le nombre de variables fini (les ). Cependant, travailler avec N! est un peu lourd : je me suis donc servi des intervalles de Farey, qui sont eux au nombre de
. Je travaille donc ensuite non pas sur l'ensemble des nombres décimaux ou réels de
, mais seulement sur l'ensemble des intervalles de Farey, ou plutôt sur des nombres décimaux représentatifs de chaque intervalle de Farey (car si
est un nombre de l'intervalle de Farey n°
alors, tous les nombres de cet intervalle peuvent remplacer
).
* Etant donné les premiers termes de la suite solution, un nombre
ne peut être le
-ème terme que si :
Pour tout (et
bien sûr) et pour tout
:
n'est pas dans le même
-ème intervalle que
.
C'est une condition nécessaire mais non suffisante bien sûr. Cela se traduit informatiquement par la condition :
, avec
= partie_entiere de X.
* On peut également remarquer qu'il suffit de vérifier la condition précédente non pas sur tous les , mais seuleument pour tous les
puis pour tous les
premiers
.
* Avec ces quelques remarques, on cherche alors par "exploration des possibilités". Etant donné qu'il y a de l'ordre de nombres candidats pour la solution d'ordre
, le calcul s'effectue assez rapidement.
Voilà désolé pour la longueur du message, mais je tenais à expliquer mon raisonnement, car celui qui a passé du temps sur cette énigme ne peut passer sous silence sa logique. Un bravo pour ceux qui auront démontré (rigoureusement, pas comme moi) le résultat. Et un merci à Minkus pour ce genre d'énigme comme j'aimerais en avoir plus souvent !
 Bonjour, je propose la suite suivante :
Bonjour, je propose la suite suivante :
 n
n
 *,
*, .
Cette suite m'a l'air de vérifier les conditions recquises pour un nombre infini d'entiers...
Merci pour l'énigme ^^
 Bon, j'ai omis le détail de "nombres décimaux" donc sauf erreur, ma suite vérifie les conditions précédentes pour tout entier n allant de 1 à 6.
Bon, j'ai omis le détail de "nombres décimaux" donc sauf erreur, ma suite vérifie les conditions précédentes pour tout entier n allant de 1 à 6.
 Un=(2n-1)/2N
Un=(2n-1)/2N
par exemple pour N=10 intervals
le terme qui appartient au 3eme interval ]2/10;3/10[
est U3=(2*3-1)/2*10=5/20=0.25
et ainsi de suite pour chaque valeur de N on a une suite Un
 on peut en écrire une infinité
on peut en écrire une infinité
le 1er : entre 1/2 et 1 exclus
le 2e : entre 1/3 et 1/2 exclus
le 3e : entre 1/4 et 1/3 exclus
le ne : entre 1/n+1 et 1/n exclus
exemple de début : 0.7 0.4 0.3 0.21 0.18 0.15 0.13 0.12 0.11 0.95
Bonjour,
Bon l'enigme (due a un certain Steinhaus) a ete poste le 17 octobre et apres un peu plus de 17 jours de reflexion, je peux vous annoncer que la reponse etait 17 !
Personnellement, j'avais la suite suivante :
0,71 / 0,09 / 0,42 / 0,85 / 0,27 / 0,54 / 0,925 / 0,17 / 0,62 / 0,355 / 0,78 / 0,03 / 0,48 / 0,97 / 0,22 / 0,66 / 0,32
Maintenant pour une demonstration il va falloir revenir 
Un grand bravo donc a Manpower, Nofutur2 et Nobody qui ont chacun adopte une methode differente.
>Manpower : Felicitations pour la reponse en image tres explicite.
>Nofutur2 : Merci pour la confirmation sur Steinhaus. Ah ce Gardner !
>Nobody : Je n'ai pas tous compris mais ca ne me surprend pas  Moi et les algorithmes !
Moi et les algorithmes !
D'autre part, je tiens a saluer le "fair-play" de Savoie et lo5707 qui ont ose donner une reponse sans certitude. lo5707, ta methode ressemble un peu a celle de Manpower. Tu aurais du pousser plus loin.
Enfin, merci aux autres pour leur participation meme si leurs erreurs ne sont pas du meme acabit.
minkus
PS :
Rien que vérifier prend un temps fou... bon courage minkus !
Bon la j'avoue que je vous ai fait confiance, surtout que trouver 17 etait deja bien difficile. Si l'idee vient a quelqu'un de verifier vos suites et s'il detecte une anomalie qu'il me le fasse savoir


 :o
:o
Alors là, j'avoue que je m'attendais plutôt à un joli  (si j'avais su...) !
(si j'avais su...) !
Aucune méthode ne permet donc d'avoir une certitude (la mienne (si on peut parler de méthode) encore moins que celle de Nofutur2 et nobody).
Etant curieux, j'ai tenté une recherche sur le net à partir de la citation de ta réponse Nofutur2, mais... je n'arrive à rien avec google.
Tu évoques une démonstration de la limite à 17. Aurais-tu un lien ou des infos sur cette démonstration ?
Enfin, merci minkus pour ta remarque... désormais j'arrête les siestes ! 
 Le lien que j'ai utilisé est le suivant (A 604)
Le lien que j'ai utilisé est le suivant (A 604) ![]() ...mais il ne comporte pas de démonstration.
...mais il ne comporte pas de démonstration.
J'ai trouvé un document extrait du Journal of the Numbers Theory de 1968, qui décrit comment arriver au résultat...mais ca m'a semblé bien compliqué pour le temps que je pouvais y consacrer..Alors, bon courage!!!.![]()
 Più... tout simple en fait ! Bon je mets ça de côté pour ma retraite ! Merci pour ces deux liens. Curieux le second ne mentionne pas ledit Warmus!
Più... tout simple en fait ! Bon je mets ça de côté pour ma retraite ! Merci pour ces deux liens. Curieux le second ne mentionne pas ledit Warmus!
PS: minkus, la faible participation à cette énigme est probablement due à l'absence d'image 
PPS: L'erreur (il me semble) de lo5707 est d'avoir déjà "ordonné" ou numéroté les intervalles, non?

PPS: L'erreur (il me semble) de lo5707 est d'avoir déjà "ordonné" ou numéroté les intervalles, non?
c'est fort possible oui, quand je vois ton schéma ca me parait plus clair
PS: minkus, la faible participation à cette énigme est probablement due à l'absence d'image

Je confirme, j'avais bien évidemment la bonne réponse mais l'absence d'image m'a décu et j'ai donc décider, pour me venger, de ne pas la poster.
 :D
:D :D
:D
Félicitations à Manpower, Nofutur2 et Nobody pour avoir trouvé

Fractal

Bonjour à tous, voici la demo,c'est par l'absurde mais accrochez vous !!
et ne demandez surtout pas d'expliquer ! lol
C'est tiré du bouquin des deux hommes qui ont solutionnés le pb.
http://jeusegment.9online.fr/document.htm
 j'ai cru voir la solution dans un mirage et j'ai été persuadé pendant deux jours que mon résultat était juste !!!
j'ai cru voir la solution dans un mirage et j'ai été persuadé pendant deux jours que mon résultat était juste !!!
Défi 94 : Partition
J'arrive longtemps après la bataille mais il me semble qu'il y a encore des choses à dire sur cette énigme passionnante.
Plusieurs ont prouvé qu'il existait une suite convenable pour N = 17 mais ceux qui ont voulu justifier qu'il n'en existe pas pour N = 18 n'ont pas l'air très satisfait de leur justification.
D'autre part, si Steinhaus n'a pas trouvé de preuve théorique, je ne pense pas être capable d'en trouver une.
Je vais donc essayer avec l'informatique.
Guillome signale une démonstration qu'il a trouvée sur le Web. Je suis allé
voir et, après m'être accroché
un moment, j'ai choisi de chercher de mon côté.
Commençons manuellement pour voir apparaître la mêthode.
Partons de x1 dans ]0, 1/2 [ et x2 dans ]1/2 , 1[ (ce n'est pas restrictif).
x3 peut se placer de 3 façons par rapport à x1 et x2 et les suites au rang 3 sont celles qui vérifient
x3 dans ]0,1/3[, x1 dans ]1/3,1/2[ , x2 dans]2/3,1[ ou:
x1 dans ]0,1/3[, x3 dans ]1/3,2/3[ , x2 dans]2/3,1[
ou
x1 dans ]0,1/3[, x2 dans ]1/2,2/3[ , x3 dans]2/3,1[
Pour une suite vérifiant la propriété au rang 4, les 3 premiers termes doivent vérifier la propriété au rang 3.
On doit donc être pour x1, x2, x3 dans l'une des trois configurations ci-dessus .
Ensuite, x4 doit s'intercaler quelque part.
Par exemple, avec la première configuration, où
x3 < x1 < x2, on cherche les solutions au rang 4 vérifiant
x4 < x3 < x1 < x2 ou x3 < x4 < x1 < x2 ou x3 < x1 < x4 < x2 ou x3 < x1 < x2 < x4.
En plus les 4 nombres doivent être sur les 4 intervalles de longueur 1/4 qui correspondent.
Par exemple, la configuration x4 < x3 < x1 < x2 impose x4 dans]0, 1/4[, x3 dans]1/4, 1/2[
etc.
x3 doit donc être dans l'intervalle ] 1/4 , 1/3 [ intersection de ]0, 1/3 [ et ] 1/4 , 1/2 [.
Par contre, x1 dans] 1/3 , 1/2 [ et x1 dans ] 1/2 , 3/4 [ sont incompatibles.
Cette configuration x4 < x3 < x1 < x2 ne convient donc pas.
On envisage ensuite x3 < x4 < x1 < x2 .
En fait, on considère les intervalles ]0, 1/4[, ]1/4, 1/2[,]1/2, 3/4[,]3/4, 1[, et, pour chacun, on l'intercale à l'endroit convenable dans la liste bien rangée des 3 intervalles au rang 3, en rognant éventuellement chacun de ces derniers.
Notons que la façon de rogner n'est pas la même suivant que l'intervalle à rogner est avant ou après le point où on intercale.
Si aucun des intervalles rognés n'est vide, on détient là une suite d'intervalles au rang 4 qui
fournirait, si on le voulait, des suites (x1, x2, x3, x4) convenables.
Tout cela se généralise de façon évidente et se programme facilement.
Il est à remarquer qu'on raisonne uniquement sur des suites d'intervalles. Les noms et valeurs des suites xn n'apparaissent pas.
Une suite d'intervalles pourra être définie par la suite des bornes inférieures et la suite des bornes supérieures, ce qui simplifie les problèmes d'intersection.
J'ai fait ça avec Maple; une trentaine de lignes peu soignées.
Après avoir vérifié sur des valeurs pas trop
grandes qu'il faisait bien ce que je voulais, je lui ai demandé d'aller jusqu'`a
18 en sortant seulement, pour
chaque n, le nombre de suites d'intervalles. Il a tourné 20 minutes et les réponses fournies sont des nombres qui apparaissent dans l'article signalé
par Guillome, notamment:
Au rang 17: 768 suites d'intervalles. Au rang 18: 0 suite d'intervalle.
Merci encore pour cette énigme!
***
1
Nombre de participations : 0
Temps de réponse moyen : 119:15:26.


