Inscription / Connexion Nouveau Sujet
Défi : fonction !
Bonjour ;
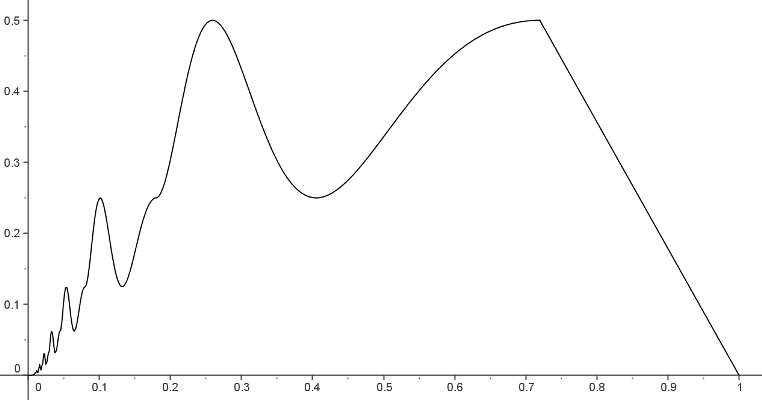
Soit une fonction continue qui prend toutes ses valeurs un nombre fini de fois .
Prouver que prend au moins une de ses valeurs un nombre impair de fois .
 bonne réflexion !
bonne réflexion !
Bonsoir, l'image continue d'un compact est un compact.
Ce qui aide à justifier l'affirmation d'elhor_abdelali
 Cliquez pour afficher
Cliquez pour afficherBonjour à tous,
Ça me rappelle un oral de l'X
Existe-t-il une fonction continue de
Ma prof m'a donné une idée de la preuve, c'est zoli !

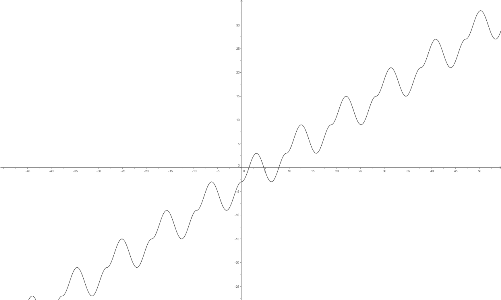
gui_tou> pour exactement deux fois, la réponse est non ; la démonstration me semble aisée, en voici le principe : si f(a)=f(b) avec a<b, f atteint son maximum sur [a;b] en c. f(c) n'est pas atteint à l'extérieur de [a;b], sinon le théorème des valeurs intermédiaires prouverait qu'une valeur est au moins atteinte trois fois par f. Donc f(c) est atteint une deuxième fois dans [a;b] : par exemple en d. f atteint son minimum sur [c;d] en e et il est facile de voir qu'une valeur est atteinte au moins quatre fois par f.
Bonjour.
Je fais remonter ce topic.
blang a montré que l'exercice proposé par elhor était faux.
Je propose cette version:
Soit f une fonction continue sur [0,1], à valeurs dans
 , strictement monotone par morceaux sur [0,1] (ce qui signifie que [0,1] est la réunion d'une famille finie de segments sur lesquels la restriction de f est strictement monotone).
, strictement monotone par morceaux sur [0,1] (ce qui signifie que [0,1] est la réunion d'une famille finie de segments sur lesquels la restriction de f est strictement monotone).
Montrer qu'il existe une valeur qui est atteinte par f un nombre impair de fois.
Bonjour à tous,
Officiel de la Taupe 2009/2010 (n°16), page 7 exercice 26 :
Soit une fonction continue de [0;1] dans R qui ne prend ses valeurs qu'un nombre fini de fois. Montrer que l'une au moins de ces valeurs est prises un nombre impair de fois.
Ecole Polytechnique-ENS Cachan - option PSI.
Je sais que ça a déjà du arriver, mais cela ne vous étonne pas qu'un sujet d'ENS soit faux ? Etes vous certain que Blang a fourni un contre exemple valable ?



 [0;1] tel que f(u)=f(v) et f(x)
[0;1] tel que f(u)=f(v) et f(x) f(u)
f(u)  x dans [u;v] (ou f(x)
x dans [u;v] (ou f(x) f(u)
f(u)  [0;1]
[0;1]