Niveau Licence-pas de math

Démonstration géométrique des dérivées sin et cos

Posté par
ferality 13-03-24 à 19:35

Bonjour,

J'essaie de retrouver une démonstation géométrique de la dérivée du $sin$ et du $cos$ vue dans une vidéo, mais je rencontre un problème.

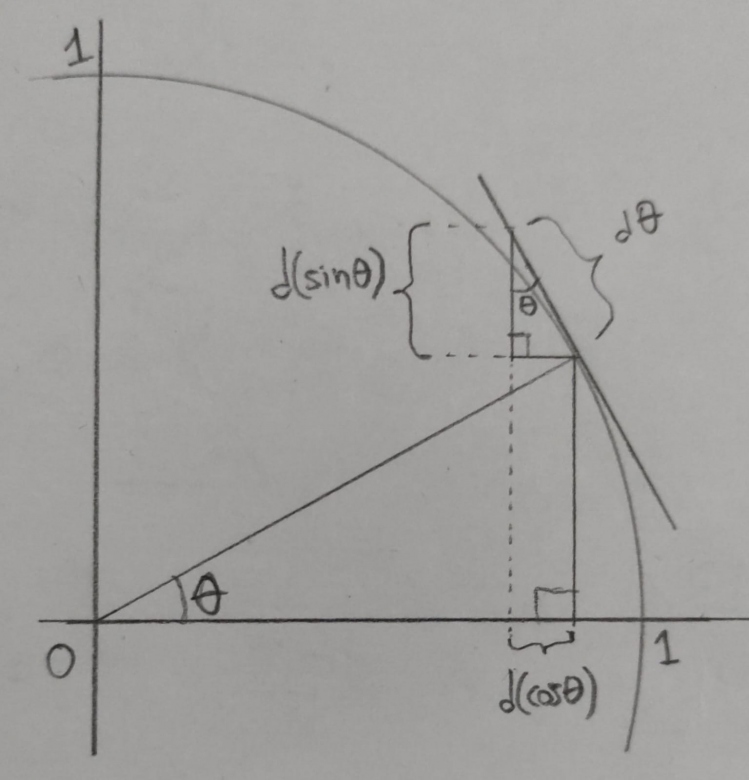
J'ai mis mon schéma en pièce-jointe. La droite oblique est la tangente au cercle trigo (non représenté), elle forme donc un angle droit avec l'hypothénuse du grand triangle.

Il faut imaginer que l'hypothénuse du petit triangle, $d\theta$ , est très petite, une quantité "infinitésimale" (qui tend vers 0, enfin le classique pour les dérivées).

Ce schéma me permet de trouver sans problème le résultat $\dfrac{d(\sin\theta)}{d\theta} = \cos\theta$ , simplement en prenant le cosinus de l'angle $\theta$

Mais quand je prend le sinus de l'angle $\theta$ , je trouve : $\dfrac{d(\cos\theta)}{d\theta} = \sin\theta$ . Or ça n'est pas bon, il manque un signe moins !

Ce que je crois ou pense comprendre :
$d(\sin\theta)$ est une quantité positive, car l'incrémentation de $\sin\theta$ , conséquence de l'incrémentation de $\theta$ par la quantité $d\theta$ "monte" dans le sens des ordonnées.

$d(\cos\theta)$ est une quantité négative, pour des raisons similaires, or on voit qu'après l'incrémentation de $d\theta$ le cosinus est plus petit qu'avant, donc forcément $d(\cos\theta)$ est négatif.

$d\theta$ étant une incrémentation de $\theta$ dans le sens de la croissance de l'angle, qui plus est dans le sens trigonométrique, est une quantité positive.

Mais tout ça ne me permet pas, à mon sens, d'arriver au résultat que je veux c'est à dire $\dfrac{d(\cos\theta)}{d\theta} = -\sin\theta$ .

Où est mon erreur ?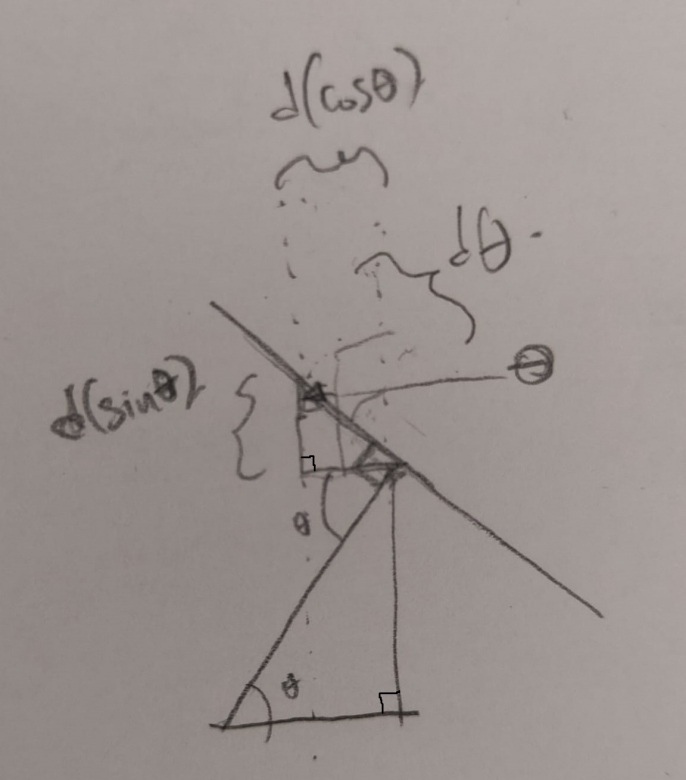

Démonstration géométrique des dérivées sin et cos

***Forum modifié en fonction du niveau indiqué dans le profil***

Posté par re : Démonstration géométrique des dérivées sin et cos 13-03-24 à 19:40

salut

schéma incompréhensible : il existe la règle et le compas ...

Posté par re : Démonstration géométrique des dérivées sin et cos 13-03-24 à 21:49

Salut, voilà le schéma mieux fait

Démonstration géométrique des dérivées sin et cos

Posté par re : Démonstration géométrique des dérivées sin et cos 14-03-24 à 12:49

Ton erreur, c'est que tu utilises la formule sinus(angle) = (longueur du côté opposé) / (longueur de l'hypoténuse) avec une longueur négative a numérateur ou au dénominateur, donc le signe du résultat est faux. Ton petit schéma illustre le fait que la valeur absolue de $\dfrac{d(\cos\theta)}{d\theta}$ est égale à la valeur absolue de $\sin\theta$ .

Pour te servir de ton schéma il faut juste réfléchir deux secondes avant :

1) sur le premier quart du cercle trigonométrique, le sinus est croissant et le cosinus est décroissant, donc $d\sin\theta = \sin(\theta+d\theta) - \sin\theta$ est du signe de $d\theta$ et $d\cos\theta$ est au contraire du signe de $-d\theta$

2) par conséquent le rapport $\dfrac{d(\sin\theta)}{d\theta}$ est positif alors que $\dfrac{d(\cos\theta)}{d\theta}$ est négatif

3) on en déduit que la valeur absolue du premier lui est égale, alors que celle du second est égale à son opposé

Là, tu appliques ta formule et ton dessin, pour en déduire que $\dfrac{d(\sin\theta)}{d\theta} = |\cos\theta|$ et $-\dfrac{d(\cos\theta)}{d\theta} = |\sin\theta|$ .
Mais à nouveau, il faut te souvenir que sur le premier quart du cercle trigonométrique, $\cos$ et $\sin$ sont toutes les deux à valeurs positives, donc les valeurs absolues sont inutiles dans le membre de droite de ces deux dernières équations

Posté par re : Démonstration géométrique des dérivées sin et cos 15-03-24 à 17:22

Bonjour,

Merci je vois un peu mieux. Si je comprends bien, le problème viens du fait que j'applique Pythagore dans un triangle qui a un de ses côtés de longueur négative car $d(\cos\theta)$ est négatif.

Il faudrait donc utiliser une "version élargie" du théorème de Pythagore pour que tout ça fonctionne bien jusqu'au bout, car en l'état le théorème de Pythagore normal ne travaille qu'avec les valeurs absolues, car une longueur négative n'a aucun sens géométriquement.

J'ai aussi pensé à l'argument suivant, qui est peut-être un peu trop raccourci :

$\dfrac{d(\cos\theta)}{d\theta}$ est négatif, et comme $\sin\theta$ est positif, alors $-\sin\theta$ est négatif, et donc $\dfrac{d(\cos\theta)}{d\theta} = -\sin\theta$ .